Стабилизация сельскохозяйственной системы «трактор-прицеп» на засоленных почвах: подход на основе совместного планирования траектории
Проектирование и промышленные инновации в области интеллектуальной сельскохозяйственной техники для засоленных почв являются важными средствами комплексного управления и повышения продуктивности таких земель. Создание автономных и беспилотных сельскохозяйственных тракторов представляет собой закономерный тренд развития интеллектуальной техники для засоленных территорий. Будучи недоопределённой системой с неголономными связями, система «трактор-прицеп» сталкивается с проблемами в области независимого планирования траектории и поперечной стабилизации на засоленных почвах.
В данном исследовании на основе нелинейных характеристик недоопределённости системы «трактор-прицеп» и закона пассивного рулевого управления прицепа была разработана модель совместного управления по двум траекториям. Путем решения кинематического/динамического пространства состояний системы было построено нелинейное ведущее звено, способное генерировать опорное положение трактора и прицепа. На основе внутреннего свойства поперечного отклонения системы предложен алгоритм совместного прогнозирования траектории, удовлетворяющий ограничениям временной области и системы. Комбинируя независимое смещение двух траекторий и параметр поперечной устойчивости системы, был создан оптимизированный по энергетической функции управляющий параметр для балансировки между точностью следования по траектории и устойчивостью поперечного управления.
Результаты экспериментов показали хорошее соответствие между прогнозируемой траекторией прицепа и траекторией совместного управления: средняя поперечная ошибка не превышала 0,1 м, а средняя ошибка по курсу не превышала 0,054 рад. Это подтверждает, что динамический контроллер, разработанный для недоопределённой системы «трактор-прицеп», способен гарантировать плавность траектории прицепа и устойчивость управления трактором на засоленных почвах.
1. Введение
Система тягача с прицепом (TTS), которая является наиболее часто используемым механическим транспортным оборудованием, применялась в комплексном управлении засоленными щелочными землями [ 1 , 2 ], перевалке сельскохозяйственной продукции [ 3 , 4 ], а также в исследовании и проектировании сельскохозяйственной техники [ 5 , 6 ]. Как правило, TTS состоит из автономно управляемого трактора и неприводного прицепа [ 7 , 8 ]. Таким образом, TTS классифицируется как недоуправляемая система, что представляет собой значительную область исследований в теории управления, особенно в отношении прогнозирования траектории и управления движением [ 9 , 10 ]. Исследование динамических характеристик TTS на основе неголономных ограничений может обеспечить решающую основу для будущих исследований, направленных на интеллектуальную разработку и промышленные инновации сельскохозяйственной техники в солено-щелочных средах [ 11 , 12 ].
Баланс между отслеживанием траектории и устойчивостью управления имеет решающее значение для безопасной работы TTS [ 13 ]. В [ 14 ] Вэнь и др. разработали стратегию управления для задач беспилотного опрыскивания, чтобы добиться эффективного управления отслеживанием пути TTS в сельскохозяйственных условиях. Этот метод повышает эффективность планирования пути опрыскивания TTS, объединяя предварительную установку опорной траектории со стратегией двойного управления. В [ 15 ] задача планирования пути для системы TTS была переформулирована как задача выпуклой оптимизации с использованием «леммы Фаркаса». Интегрируя ограничения дорожной среды и системы транспортных средств в неравенства, был разработан планировщик движения TTS. В [ 16 ] стоимость планирования системы была всесторонне оценена путем создания уравнения энергетической функции, которое интегрирует параметры состояния TTS, такие как потребление энергии, сила и ограниченное состояние. Это открывает новые перспективы для управления системой TTS. Однако необходимы улучшения проходимости и адаптивности системы, особенно при выполнении крутых поворотов [ 17 , 18 , 19 ].
В [ 20 ] была предложена структура для оценки уклона дороги и массы, которая учитывает изменения угла тангажа. Эта структура разрабатывает физически осуществимый оценщик угла тангажа на основе нейронной сети для оценки эффекта тангажа в данных датчика продольного ускорения. В [ 21 ] Чжоу и др. реализовали механизм помощи при рулевом управлении на тракторе. Активно регулируя положение трактора, система обеспечивает точное отслеживание траектории. В [ 22 ] был представлен алгоритм оценки состояния TTS, использующий историческую информацию о состоянии от трактора. Объединяя оценку состояния TTS с наблюдениями в реальном времени, прогнозируемая траектория была реконструирована и уточнена. В [ 23 ] статистические результаты пассивных углов рулевого управления были использованы для моделирования динамики движения TTS. Из-за низких скоростей эти исследования в основном сосредоточены на кинематических характеристиках TTS [ 24 ].
Также были предприняты попытки интегрировать прогнозирование траектории TTS с методами глубокого обучения. В [ 25 ] для расчета угла направления использовался управляемый рекуррентный блок, в то время как наблюдатель измерял угол шарнира. Впоследствии оценка движения и компенсация ошибок выполнялись с использованием фильтра Калмана. Этот подход в первую очередь фокусируется на состояниях тягача и прицепа, но уделяет недостаточно внимания восприятию и взаимодействию между TTS и дорогой. В [ 26 ] была разработана структура машинного обучения, основанная на статистике параметров TTS, для облегчения прогнозирования и управления траекториями системы. Однако этот алгоритм по-прежнему требует значительного количества экспериментальных данных для эффективного обучения и проверки [ 27 ].
Ученые провели обширные исследования стратегий автонавигации TTS [ 28 , 29 , 30 ]. Однако существует ограниченное количество исследований и разработок, посвященных применению TTS на фермах по выращиванию солончаковых почв с засоленными почвами [ 31 , 32 , 33 ]. Большинство исследований в основном сосредоточены на точности отслеживания TTS в условиях низкой скорости [ 34 , 35 ]. В высокоскоростных сценариях эти стратегии управления, как правило, чрезмерно акцентируют внимание на эффективности отслеживания прицепов по отдельным траекториям. Следовательно, траектория прицепа может стать прерывистой и трудно предсказуемой, что создает риски для безопасности перегруженных TTS [ 36 , 37 ].
В данном исследовании предлагается интеллектуальная схема управления для сельскохозяйственной системы тягача с прицепом, которая представляет собой типичную систему с неполным приводом. Для решения задачи управления устойчивостью системы тягача с прицепом (TTS) предложены стратегия совместного прогнозирования по двум траекториям и метод управления боковой устойчивостью. Проанализировано построение динамической модели в условиях высокой скорости и разработано решение задачи согласованности «лидер-ведомый» с учетом дискретных положения и скорости во временной области. Разработана схема оценки и управления боковой устойчивостью путем интеграции высокоскоростных и низкоскоростных двухветвевых структур. Основные результаты данного исследования:
Для решения проблемы недостаточной управляемости сельскохозяйственной системы тягача с прицепом, работающей на засоленных солончаковых почвах, была разработана кинематическая/динамическая модель, использующая представление нелинейных автономных систем с неголономными связями в пространстве состояний. Эта модель служит основой для дискретного математического представления и вычислительного анализа состояний системы;
Объединяя разработку динамической модели с дискретизацией системы первого порядка во временной области, мы предлагаем метод совместного планирования с двумя траекториями для TTS. Этот подход проясняет характеристики и поведение внутренней разницы в положении колёс (IWD) в недостаточно активизированной TTS. Кроме того, мы представляем решатель, разработанный для решения проблемы рандомизации ошибок IWD и непредсказуемости траекторий движения прицепа, часто встречающейся в традиционных методах. Наш динамический анализ и ограничения состояния, основанные на алгоритме совместного планирования траекторий, обеспечивают предсказуемое и количественно определяемое планирование траекторий движения прицепа;
Предлагается контроллер стабилизации поперечной ошибки для системы тягача с прицепом, основанный на двухтраекторном совместном планировании. В отличие от предыдущих разработок, эта схема управления полностью учитывает характер движения и поперечное положение прицепа в системе TTS. В результате достигается эффективный баланс между устойчивостью системы и сохранением траектории.
2. Пространство состояний системы «тягач-прицеп»
В этом разделе представлена схема построения кинематической/динамической модели TTS. Для достижения характеристик замкнутой обратной связи в TTS была разработана модель плоскости рыскания.
2.1. Наблюдаемая и управляемая модель трактора
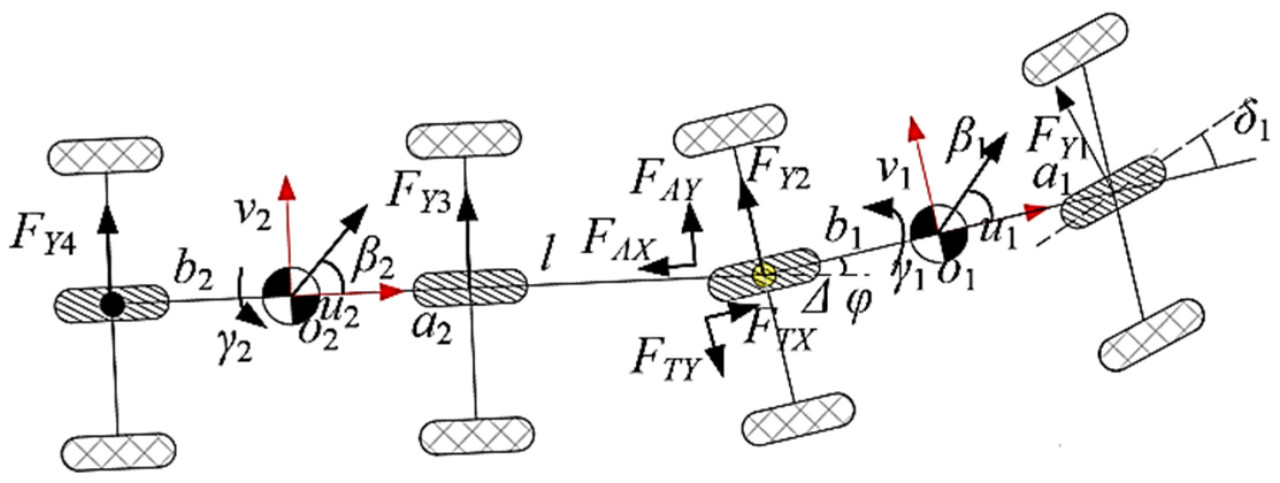
При строительстве сельскохозяйственных прицепных инженерных машин, предназначенных для засоленных солончаков, в качестве тягача использовалось заднеприводное транспортное средство, а прицеп был безмоторным (как показано на рисунке 1 ).
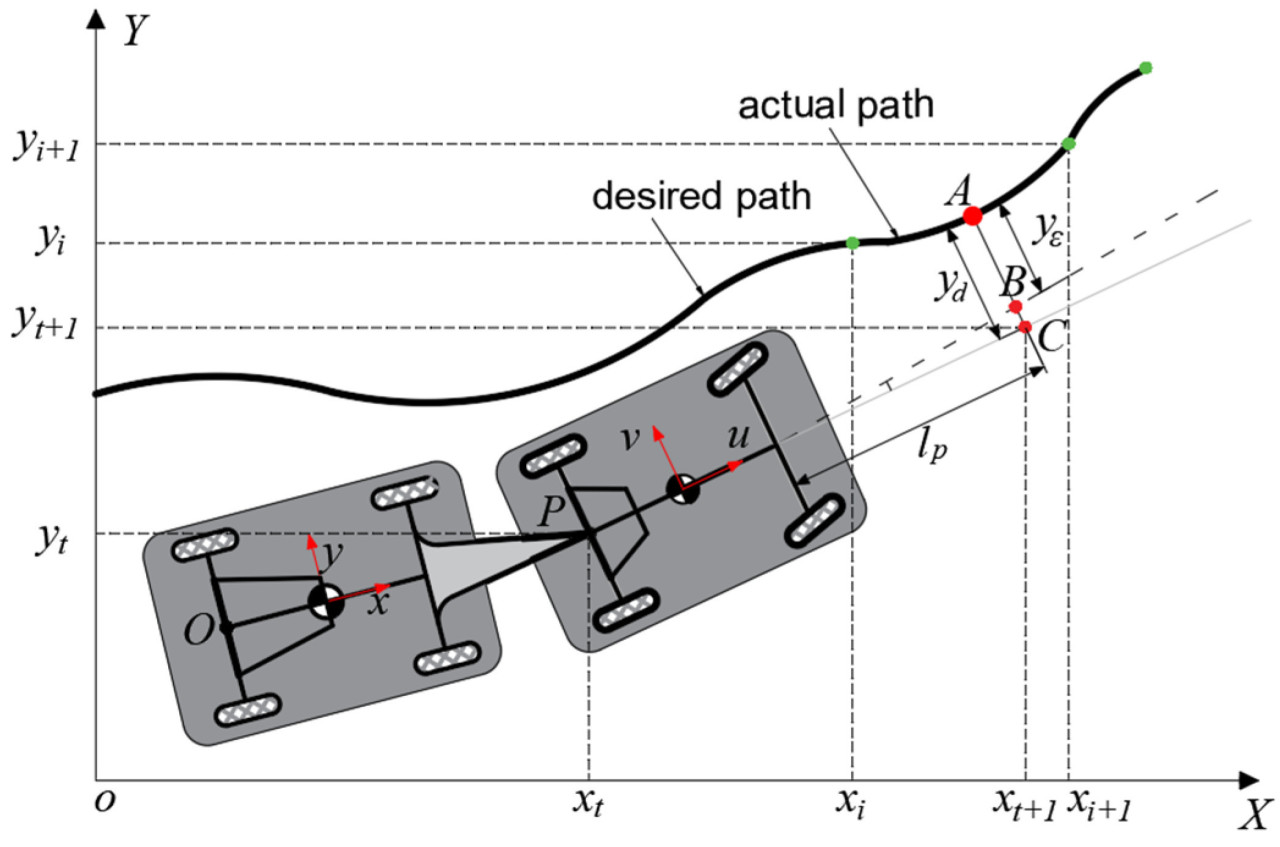
В данном исследовании установлено, что кинематические характеристики TTS в первую очередь исследуются на низких скоростях [ 38 ]. Однако с увеличением скорости динамические характеристики становятся основным фактором, влияющим на поведение TTS в движении [ 39 ]. Поэтому в данном исследовании была разработана кинематическая модель. Для облегчения решения задачи о состоянии системы в качестве опорной точки для расчета координат положения использовалась середина задних осей TTS (символы P и O ).
Здесь yd — ошибка между положением транспортного средства и заданной траекторией; yε — расстояние между результатом предварительного просмотра и запланированной траекторией после регулировки угла передних колес; v и u — ортогональные компоненты разложения скорости в системе координат транспортного средства соответственно; l p — расстояние предварительного просмотра.
Входные данные системы управления в традиционных системах управления можно представить как состояние движения системы, однозначно определяемое углом рыскания на определённых скоростях. Решение для величины управления курсовым углом выглядит следующим образом:
Уравнение (3) можно получить из преобразования Лапласа:
Ряд Тейлора использовался для расширения уравнения приближенного решения низкого порядка следующим образом:
Для получения дифференциального уравнения первого порядка для входного сигнала рулевого управления было выполнено обратное преобразование Лапласа.
Это математическое описание управляющей величины трактора. Ввиду малости старшего члена ошибки и того факта, что результаты расчётов динамически обновлялись и учитывались, старшего члена ошибки можно игнорировать.
2.2 Кинематическая модель сцепки «тягач-прицеп»
В целом, входные сигналы системы транспортного средства можно представить как управление направлением и скоростью. Таким образом, разработанная в данном исследовании модель TTS представляет собой плоскую модель, которая игнорирует факторы, влияющие на систему транспортного средства, такие как скачок тангажа и сопротивление воздуха во всех направлениях в реальных условиях эксплуатации. Курсовой угол и скорость системы можно наблюдать и контролировать, а явление складывания кузова транспортного средства не происходит.
Математическое выражение состояния движения системы представлено в уравнении (6) (для уравнения кинематики некоторые параметры на рисунке 2 являются избыточными):
Состояние TTS можно полностью представить с помощью указанных выше параметров и известных параметров:
Координаты точки P(𝑥'𝑗, 𝑦'𝑗) можно обновить и получить:
A 1 и A 2— это матрица параметров, а∆𝑠𝑗является дискретным шагом прицепа.
2.3. Модель динамики системы «тягач-прицеп»
На основе характеристик недостаточного срабатывания TTS была дополнительно разработана линейная модель плоскости рыскания для динамики на основе переходной модели (как показано на рисунке 2 ).
В уравнениях (11)–(14)m i — масса тягача или прицепа; I zi — момент инерции; v i — боковая скорость; u i — продольная скорость; 𝛾𝑖 — угловая скорость вращения тягача или прицепа вокруг центра масс. F Y1, F Y2, F Y3 и F Y4 — боковые силы, действующие со стороны земли на шину. F AX, F AY, F TY и F TX — сила действия и противодействия (через ортогональное разложение), создаваемые буксирным рычагом. a i и b i — длина от центра передней оси и центра задней оси до центра тяжести тягача или прицепа. 𝛿𝑖 — углы поворота рулевого колеса TTS. Среди них i = 1, 2.На основе продольной линейной модели шин боковую силу, действующую со стороны земли на шины, можно выразить следующим образом:
Где C i (i = 1, 2, 3, 4) — коэффициент сопротивления качению между шиной и дорожным покрытием, а точка зрения водителя используется в качестве точки отсчёта для унификации системы координат транспортного средства. Согласно руководству по инструменту, C i = 0,035 [40]. TTS связана шарнирным соединением, и уравнение механической связи между ними выражается следующим образом:
Уравнение кинематической связи для TTS выглядит следующим образом:
Мгновенное состояние системы можно рассматривать как равномерную скорость, и можно записать следующее уравнение:
Кроме того, между γ 1иγ 2можно получить следующее соотношение:
Через (19)–(24), 𝑥 = [ 𝜆 1, 𝛾1, 𝛾2, ∆ 𝜑 ]. Уравнения состояния TTS можно выразить следующим образом:
Подробная информация о каждом определении матрицы (25) приведена в Приложении А.
3. Боковой стабилизатор, основанный на прогнозировании двойной траектории
Для решения задач нелинейного управления сельскохозяйственными системами тягачей и прицепов на засоленных солончаковых почвах в данном разделе представлен контроллер боковой стабилизации, использующий двухтраекторное планирование. Конструкция этого контроллера требует баланса между боковой устойчивостью управления TTS и ошибкой боковой регрессии при установившихся маневрах.
3.1. Совместное планирование по двум траекториям
На основе TTS был разработан коллаборативный алгоритм с двумя траекториями, как показано в Алгоритме 1. Параметры, необходимые для ввода и инициализации системы, включают параметры TTS, глобальные координаты, информацию об ориентации и опорную траекторию. Алгоритм выдаёт траекторию прицепа, положение системы и параметры управления.
Алгоритм 1. Ядро алгоритма планирования траектории с двойным взаимодействием
Входные данные: настройка параметров платформы TTWR ( a1 , b1 , a2 , b2 , IZ1 , IZ2 ) ,
начальное положение TTWR ( xi , yi ) , ( xj , yj
), длина тягового рычага l ,
максимальный угол рыскания тягача δm a x и дискретизированный
начальный путь. Выходные данные : путь V двойной
совместной траектории и переменная состояния .
𝑥 = [𝜆1 𝛾1 𝛾2 ∆ 𝜑 ]
1: Инициализация системы: базовый путь Path I =
{ P set [0], P set [1],
⋯, P set [end]},
траектория прицепа Path J = { NULL },
совместная траектория Dual-collaborative Path = { Path I , Path J },
начальный угол направления δ 1 , δ 2
2: Если P set [0] ≠ P set [end]
или Distance > 0,03
3: Пока Distance > 0,03 м do
4: Рассчитать текущее положение тягача и прицепа O и P
5: Обновить длину шага Δ s i , Δ s j → uT и
кривизну тягача ρ i , ρ j
6: Обновить координаты тягача ( x i , y i ),
новый угол направления тягача δ 1 , новый угол рыскания тягача δ 2
7: Рассчитайте скорость𝛾𝑖 ( i =
1,2) тягача или прицепа вращается вокруг центра масс O i ( i = 1,2),
боковое скольжение𝜆𝑖( i = 1,2) угол и
обновление
8: обновление координат прицепа ( x j , y j ),
новый угол направления прицепа δ 1 , δ 2
9: расчет отклонения e 1 , e 2
10: если расстояние между прицепом и границей дороги ≤
0
11: обновление пути I
12: перерыв
13: сохранение текущего положения пути J =
{ P set [0], P set [1],
⋯, P set [ k −
1], P set [ k ]}
14: иначе
15: достижение конечной точки
16: создание пути совместной траектории V = { Path I , Path J }
Где Distance — расстояние между текущим положением тягача и конечной
точкой,
e 1 и e 2 —
отклонение между колеей тягача и колеей прицепа.
Положение TTS рассчитывалось с помощью численного решения динамической модели. В процессе движения TTS регистрировались параметры состояния для текущего и последующих шагов. Параметры системы подчиняются правилу «первым вошел – первым вышел» и итерируются во времени. Процесс обновления состояния TTS был дискретизирован по временной шкале, а процесс итерации и выборки выглядел следующим образом.
3.2. Конструкция регулятора боковой устойчивости
На основе состояния TTS мы дополнительно оптимизировали стратегию управления моделью. В традиционных исследованиях эффективность отслеживания тягача и прицепа в TTS оценивалась единообразно на основе конкретных траекторий. В отличие от традиционных методов, определение TTS и прогнозирование двухколлаборативных траекторий обеспечивают более надежную основу для расчета бокового смещения следования по траектории (PFLO). PFLO относится к боковому отклонению между каждым независимым кузовом транспортного средства (тягачом и прицепом) и их соответствующими траекториями. В данном случае PFLO каждого кузова транспортного средства рассчитывалось независимо и оценивалось комплексно.
Для улучшения установившихся характеристик TTS на высоких скоростях боковое ускорение рассматривалось как ещё один контрольный показатель. RWA представляет собой отношение бокового ускорения прицепа к боковому ускорению тягача и тесно связано с боковой устойчивостью. В данном исследовании для удобства расчётов точка отсчёта RWA была размещена на задней оси TTS. Математическое описание RWA =[𝑎𝑦 1,𝑎2]𝑇 выглядит следующим образом:
где М 1 = [u, 0, 0, 0]; Ф 1 = [0,u, 0, 0]; М 2 = [u,−(б 1+в),−(а 2+d), 0] и F 2 = [0, 0,u, 0].
Угол поворота рулевого колеса определяется ошибкой между положением системы и заданной траекторией. Следовательно, уравнение (27) можно дискретизировать:
На основе PFLO и RWA функция бокового стационарного управления и оценкиCoсистемы может быть выражена следующим образом:
![<span class="html-italic">W </span>21 — вес боковой ошибки слежения PFLO; <span class="html-italic">W </span>22 и <span class="html-italic">W </span>23 — веса бокового ускорения тягача и прицепа; <span class="html-italic">W </span>24 — вес угла рыскания прицепа; <span class="html-italic">L </span>1 = [<span class="MathJax"><span class="math"><span class="mrow"><span class="semantics"><span class="mrow"><span class="msub"><span class="mrow"><span class="mi">𝐼</span></span><span class="mrow"><span class="mrow"><span class="mn">4 </span><span class="mo">× </span><span class="mn">4</span></span></span></span><span class="msub"><span class="mrow"><span class="mi">𝑂</span></span><span class="mrow"><span class="mn">4 </span><span class="mo">× </span><span class="mrow"><span class="mo">(</span><span class="mn"> 2</span></span><span class="mi"> 𝑛 </span><span class="mrow"><span class="mo">+ </span><span class="mn">2 </span><span class="mo">)</span></span></span></span></span></span></span></span></span>], <span class="MathJax"><span class="math"><span class="mrow"><span class="semantics"><span class="mrow"><span class="msub"><span class="mrow"><span class="mi">𝐼</span></span><span class="mrow"><span class="mrow"><span class="mn">4 </span><span class="mo">× </span><span class="mn">4 </span></span></span></span></span></span></span></span></span>является единичной матрицей 4 × 4; и <i>O</i><span class="MathJax"><span class="math"><span class="mrow"><span class="semantics"><span class="mrow"><span class="msub"><span class="mrow"><span class="mn">4 </span><span class="mo">× </span><span class="mrow"><span class="mo">(</span><span class="mn"> 2</span></span><span class="mi"> 𝑛 </span><span class="mrow"><span class="mo">+ </span><span class="mn">2 </span><span class="mo">)</span></span></span></span></span></span></span></span></span>4<span class="MathJax"><span class="math"><span class="mrow"><span class="semantics"><span class="mrow"><span class="mo">×</span></span></span></span></span></span>(2<span class="html-italic">n</span>+ 2) нулевая матрица. ](https://storage.agriexpert.ru/storage/images/articles/5560/block/69499/model/xl/S0LDRpbPAkTg.jpg)
Матрицу усиления G com можно получить, используя метод экстремального Лагранжа для минимизации функции стоимости Co. Оптимизированный угол поворота рулевого колеса TTS можно выразить следующим образом:
Чтобы проиллюстрировать процесс реализации стратегии совместного управления с двойной траекторией, на рисунке 3 представлена блок-схема реализации. На основе наблюдений за фактическими и ожидаемыми положениями TTS были оценены отклонения e 1 и e 2 между фактическим и желаемым пути. Затем значения отклонения e 1 и e 2 были переданы обратно в модель управления для получения угла поворота δ 1 . Используя δ 1 в качестве входных данных функции стоимости, модифицированное оптимальное решение δ 1 com было рассчитано в соответствии с алгоритмом совместного прогнозирования траектории и контроллером боковой устойчивости PFLO. Когда TTS проходит шаг, в сочетании с входными данными δ ′ 1 com с предыдущего шага новая информация о состоянии для TTS обновлялась, и система снова решалась для нового δ 1 . Таким образом, был достигнут процесс управления с обратной связью. Кроме того, учитывая оценку риска опрокидывания на высокой скорости, в качестве ограничения была введена эмпирическая максимальная корректировка угла рыскания в размере 10°. В данном исследовании в качестве порогового значения между высокой и низкой скоростью использовалась скорость 30 км/ч. Система, превышающая 30 км/ч, классифицируется как высокоскоростная, а система, падающая ниже 30 км/ч, классифицируется как низкоскоростная.
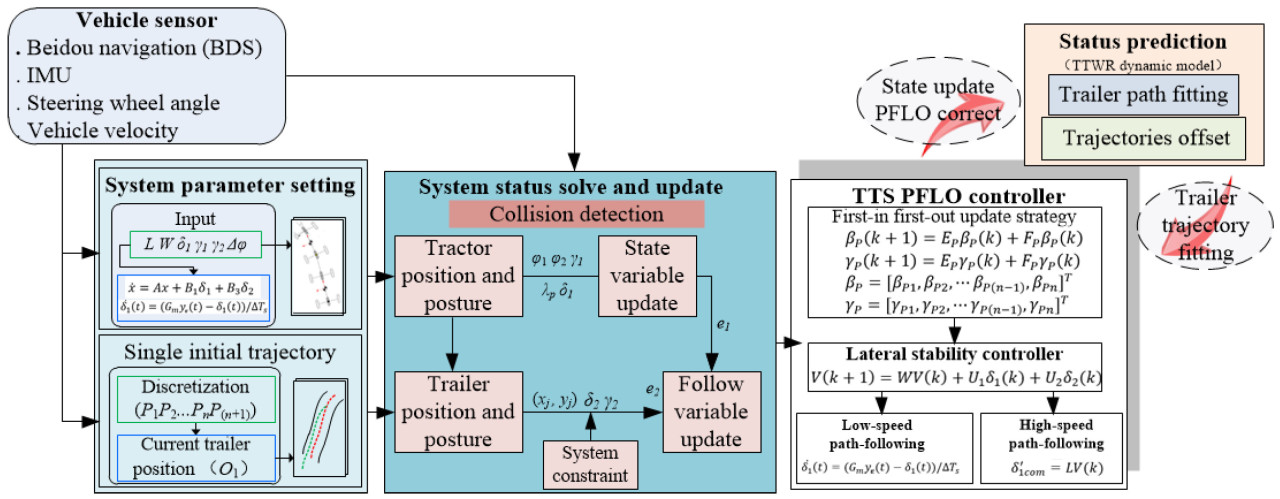
4. Экспериментальные результаты и обсуждение
4.1. Конструкция экспериментальной системы «тягач-прицеп»
На основе солончаковой сельскохозяйственной TTS была разработана недостаточно приводимая интеллектуальная экспериментальная платформа, как показано на рисунке 4. Похожая по структуре на сельскохозяйственную TTS, интеллектуальная экспериментальная платформа состоит из двух компонентов: автономно управляемого трактора и неприводного прицепа. Трактор обеспечивает питание системы, а прицеп обеспечивает грузоподъемность системы. Ее конфигурация следующая: Размер трактора составляет 970 мм × 680 мм × 400 мм. Размер прицепа такой же, как у трактора. Тяговый рычаг (расстояние между трактором и прицепом) составляет 0,4 м. Конфигурация промышленного управляющего компьютера TTS следующая: Система настроена на Linux 20.04 и ROS-noetic. Материнская плата оснащена процессором Intel i7-13700 K и 256 ГБ оперативной памяти.
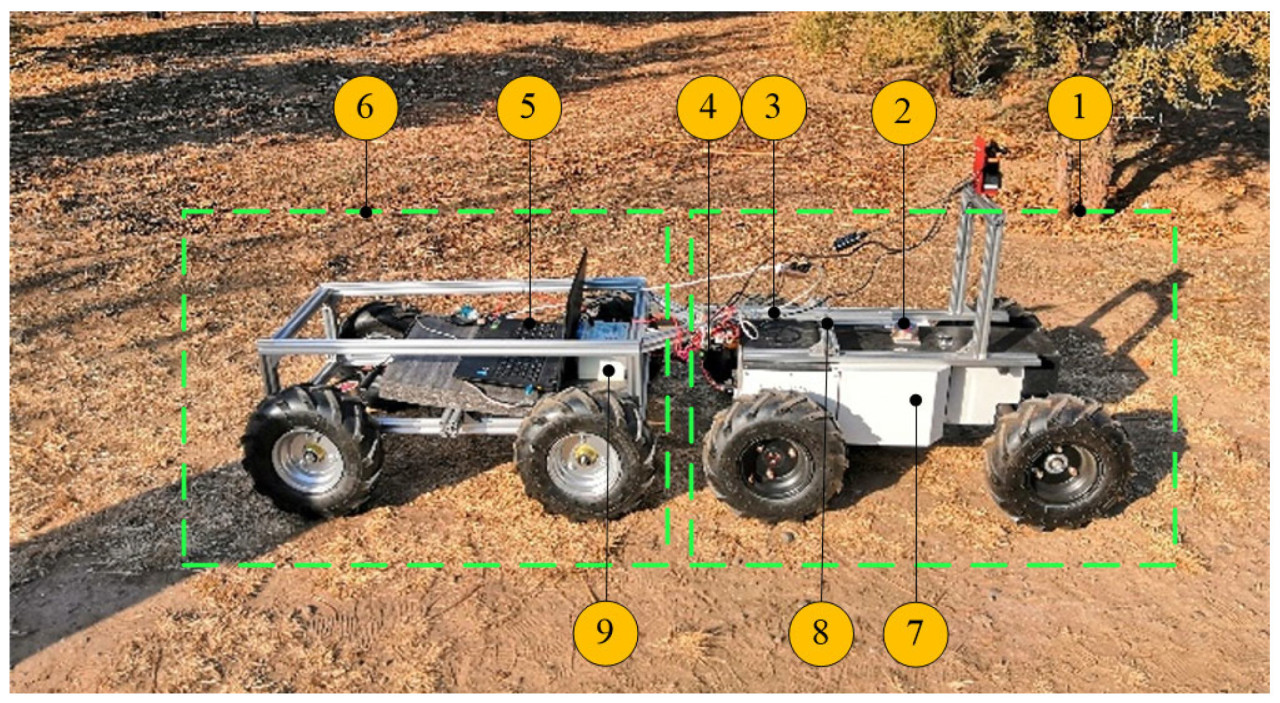
Для обеспечения точного определения положения и ориентации системы TTS в систему интегрирован модуль «Навигационная спутниковая система Beidou (BDS) + Инерциальные измерительные блоки (IMU)». В качестве инерциального измерительного блока (IMU) используется модель RION TL-740D. Архитектура сбора, хранения и передачи сигналов интегрирована в программную систему. Для каждого датчика определены каналы и узлы для публикации и подписки сигналов. В частности, измерение угла поворота рулевого колеса осуществлялось благодаря совместной работе рулевого механизма и углового энкодера, а обратная связь по скорости обеспечивалась как от GPS-приемника, так и от инерциального измерительного блока (IMU). Эта конфигурация обеспечивает критически важную обратную связь и справочную информацию для системы. Грузоподъемность TTS составляет не менее 100 кг, а максимальный угол рыскания трактора составляет 40°.
4.2 Совместное планирование траектории движения тягача с прицепом
В ходе эксперимента начальный путь был загружен в TTS как BDS, которая служила частью начальных входных данных системы. Рисунок 5 иллюстрирует эксперимент по совместному планированию с двойной траекторией на основе TTS-KM (кинематическое моделирование системы тягача с прицепом) и TTS-DM (динамическое моделирование системы тягача с прицепом). Модели кривых полос, соответствующие четырем графикам, составляли 120° ( Рисунок 5 a), 90° ( Рисунок 5 b), 60° ( Рисунок 5 c) и 180° ( Рисунок 5 d) соответственно, с радиусом поворота 4,8 м. Синяя кривая представляет собой границу дороги; толстая желтая кривая указывает на опорную траекторию. Зеленая кривая сгенерирована TTS-KM на низкой скорости. Тонкая желтая кривая иллюстрирует траекторию, предсказанную с использованием динамической модели, предложенной в данном исследовании. Важно отметить, что для ясности и удобства расчетов как зеленая, так и толстая желтая кривые были построены на основе траектории движения левого заднего колеса прицепа, а не середины задней оси или центра тяжести.
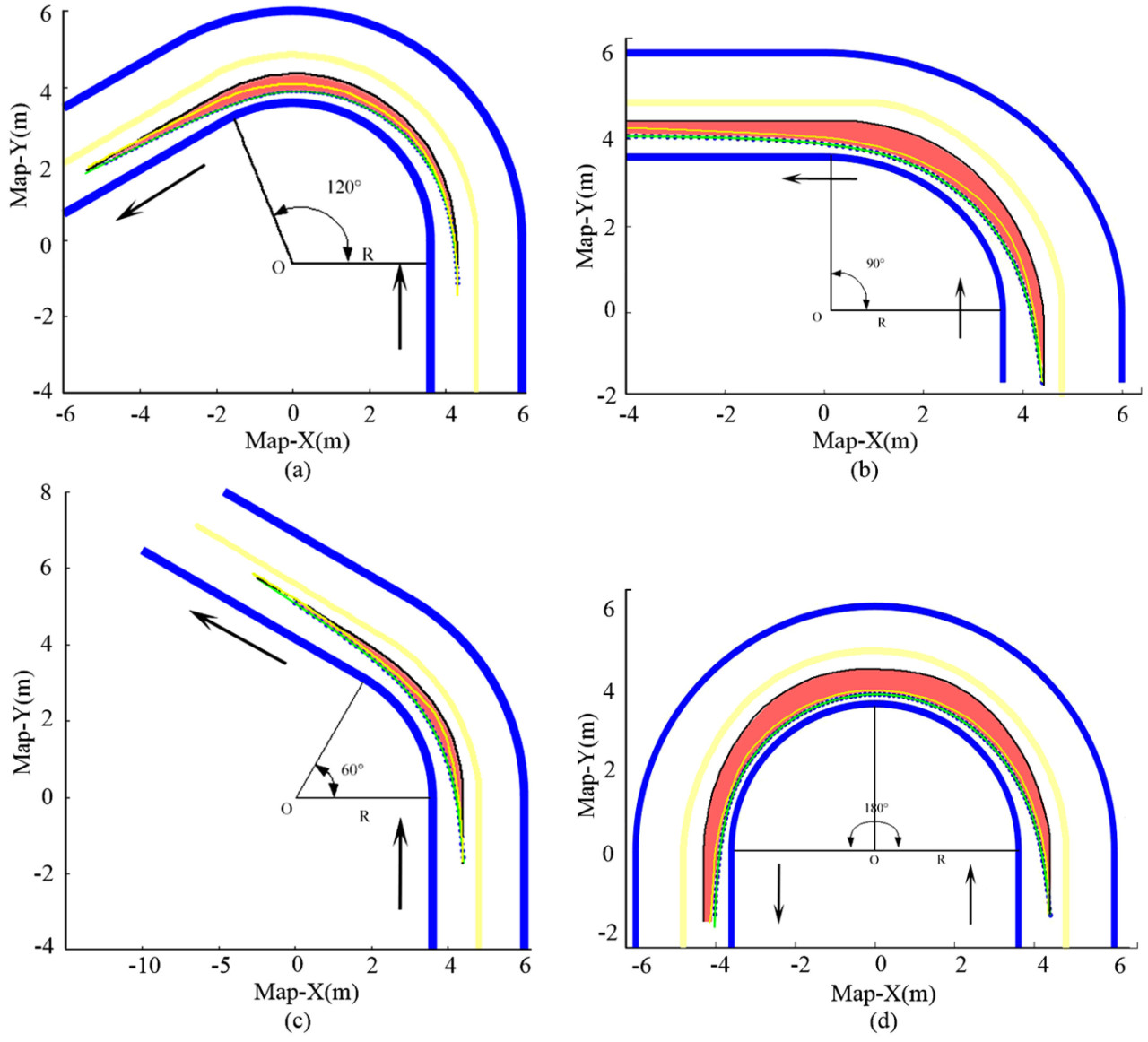
Как показано на рисунке 5 , тонкая желтая кривая не точно совпадает с зеленой кривой и, как правило, находится между зеленой и черной кривыми. Система демонстрирует улучшенную продольную устойчивость и эксплуатационные характеристики, когда TTS работает на высоких скоростях. Однако тонкие желтая и зеленая кривые расположены относительно близко друг к другу. Эта близость возникает из-за того, что больший угол поворота усиливает влияние точки шарнира на боковое сцепление прицепа, что приводит к более выраженному боковому смещению. Очевидно, что независимо от того, работает ли система на высоких или низких скоростях, боковое смещение прицепа остается ограниченным в определенном диапазоне, определяемом верхним и нижним пределами. Кроме того, сравнение прогнозируемых траекторий обоими методами взаимно подтверждает объективность и предсказуемость явления IWD в TTS.
4.3 Анализ закона бокового смещения прицепа
Для повышения точности и наглядности индуктивных результатов было проведено несколько дополнительных групп экспериментов. Результаты бокового перемещения прицепа в ходе этих экспериментов были статистически представлены (см. рисунок 6 ). Эксперименты проводились по принципу контролируемых переменных. За исключением чёрной кривой, угол поворота во всех экспериментах был установлен равным 180°, при этом варьировался только радиус поворота.
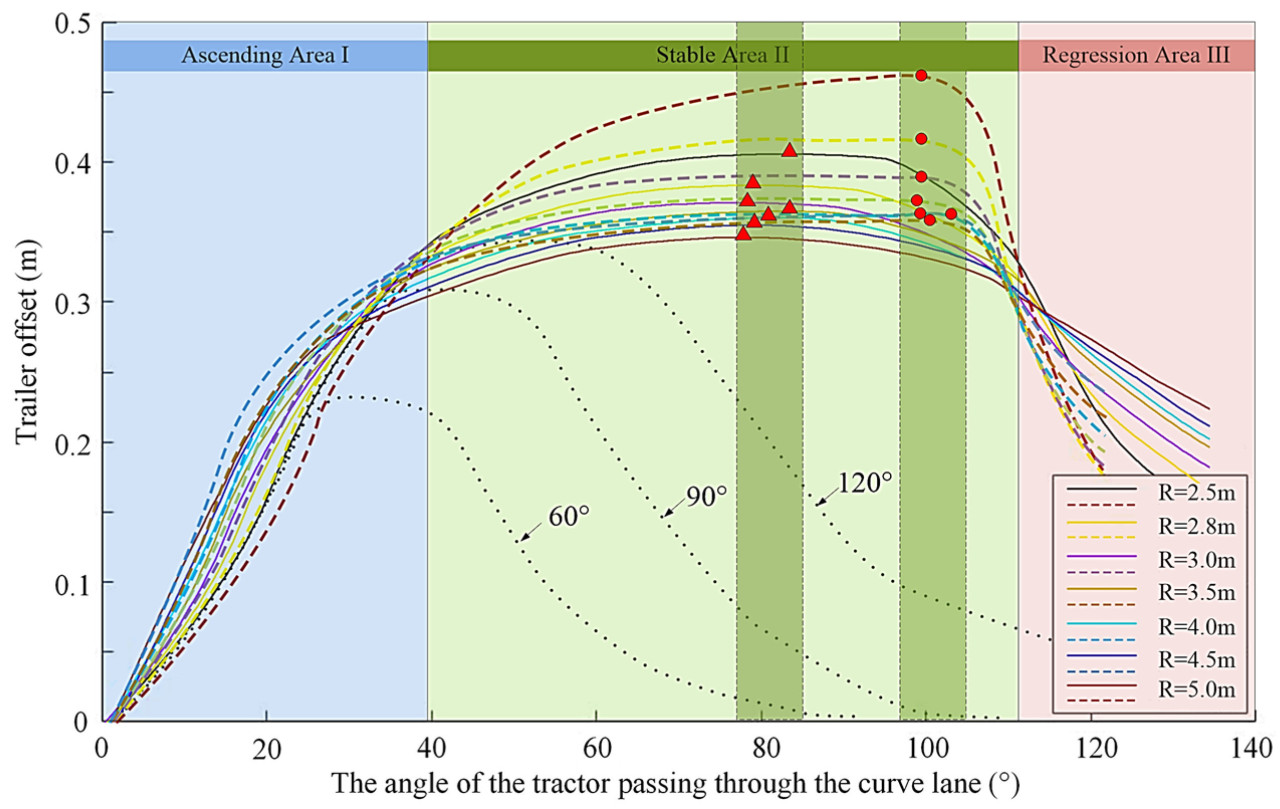
Кривая, изображенная на рисунке 6, была разделена на три области, обозначенные I, II и III, которые соответствуют трем стадиям бокового смещения прицепа. Область I - это стадия быстрого увеличения бокового смещения прицепа. На этой фазе тягач начинает входить в поворот, а прицеп постепенно следует за ним под влиянием тяги тягача. Этот эффект тяги в первую очередь отражается в его влиянии на продольную скорость прицепа. Затем система переходит в область II. На этом этапе TTS полностью входит в поворот, и уклон кривой уменьшается; однако боковое смещение прицепа продолжает увеличиваться, в конечном итоге достигая своего максимального значения. В области III боковое смещение прицепа быстро уменьшается. На этой фазе тягач начинает выходить из поворота, и траектория прицепа постепенно сходится с траекторией тягача, пока они не перекроются.
На рисунке 6 пунктирная линия соответствует результатам TTS-KM. Сплошная линия – результаты TTS-DM. На рисунке наглядно показано, что при заданном угле поворота 180° меньший радиус поворота приводит к большему экстремальному значению кривой. Красные треугольники и красные круги обозначают максимальные положения каждой кривой, которые представляют собой максимальное боковое смещение. На кривой 180° максимальное смещение прицепа происходит (с TTS-DM) в интервале 77–86° при входе в кривую (диапазон тёмно-зелёного интервала). В отличие от TTS-KM, максимальное смещение (точка экстремума) происходит в диапазоне от 96° до 105°. Это расхождение может быть обусловлено двумя факторами. Во-первых, из-за высокой скорости тягача направление тягового усилия быстро меняется в процессе поворота, в результате чего продольная сила, действующая на тягач, быстро преобразуется в поперечную составляющую после разложения. Во-вторых, в процессе расчёта высокая скорость приводит к смещению точки предварительного просмотра вперёд, что приводит к более раннему достижению максимального бокового отклонения. Результаты прогнозирования подтверждают, что эффект смещения прицепа является внутренней характеристикой системы и может быть точно спрогнозирован.
Кроме того, в качестве примера мы взяли чёрную сплошную линию (с радиусом поворота 2,5 м и углом поворота 180°). Мы сохранили радиус поворота 2,5 м, изменяя углы поворота до 60°, 90° и 120° (показаны тремя пунктирными линиями). Эти изменения показывают, что при фиксированном радиусе поворота меньший угол поворота приводит к уменьшению бокового отклонения и снижению точки экстремума.
4.4 Результаты контроля боковой устойчивости
На основании вышеописанных экспериментов алгоритм в данном исследовании был предварительно проверен. Впоследствии алгоритм был реализован на нашей экспериментальной платформе TTS для дальнейшей оценки его инженерной осуществимости. Как показано на рисунке 7 , результаты испытаний прототипа сравнивались и анализировались относительно прогнозируемой траектории. Пунктирные пурпурные линии представляют собой предварительно заданные эталонные траектории. Голубая кривая изображает траекторию, предсказанную алгоритмом. Черная и зеленая кривые представляют собой фактическую беговую дорожку на низкой и высокой скорости соответственно. Следует отметить, что, помимо пурпурной кривой, остальные кривые описывают траекторию движения прицепа. Траектория была определена с использованием встроенного модуля BDS-RTK с частотой дискретизации 200 Гц.
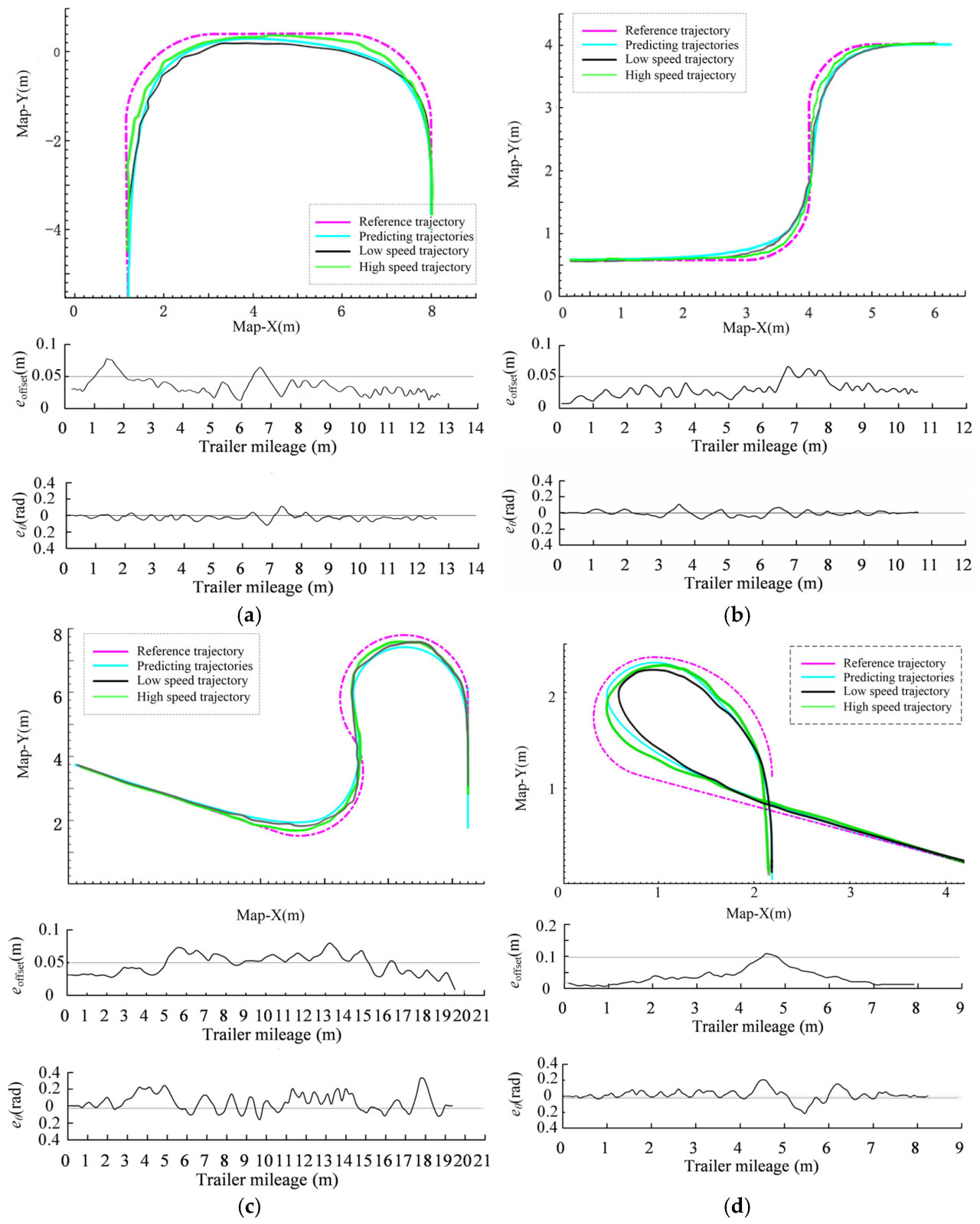
Очевидно, что, хотя чёрная и синяя кривые демонстрируют большую согласованность, траекторию движения прицепа можно расположить между прогнозируемой кривой и эталонной траекторией, адекватно отвечая требованиям слежения и управления. Зелёная кривая ближе к пурпурной кривой, что указывает на превосходную эффективность поперечного слежения прицепа на высоких скоростях по сравнению с низкими скоростями. Это наблюдение можно объяснить двумя факторами: во-первых, малый установленный радиус поворота близок к минимальному радиусу поворота TTS, в результате чего прогнозируемая траектория движения прицепа в предельных условиях очень похожа на траекторию движения на низкой скорости. Во-вторых, относительно земли прицеп неизбежно демонстрирует небольшое боковое скольжение в направлении пурпурной кривой. При достаточном трении это незначительное боковое скольжение прицепа остаётся контролируемым.
На рисунке 7 ( а–с) кривые e offset показывают тенденцию изменения бокового смещения прицепа во время движения, где по оси x отложен пробег. По оси y отложена погрешность между боковым смещением и прогнозируемой траекторией. Тенденции изменения фактического угла курса прицепа обозначены как e θ . Видно, что отклонение между алгоритмом, предложенным в данном исследовании, и фактической траекторией прицепа составляет менее 0,1 м. Отклонение между курсовыми углами обычно не превышает 0,2 рад.
На рисунке 7 d мы пытаемся управлять шасси Ackerman на высокой скорости, поддерживая минимальный радиус поворота приблизительно 1,5 м и скорость 18 км/ч. Из соображений безопасности эта скорость была уменьшена по сравнению с предыдущим экспериментом с тремя группами. Этот тест представлял собой экстремальные условия. Было заметное расхождение между фактической траекторией движения как в условиях низкой, так и высокой скорости и прогнозируемой траекторией. Тягач и прицеп, казалось, складывались во время движения. Фактически, во время движения TTS риск складывания кузова транспортного средства или опрокидывания легко возникает на таких дорогах на высоких скоростях и этого следует избегать. Согласно статистическим результатам, среднее смещение составило приблизительно 0,075 м (не более 10 см). Для угла курса прицепа среднее смещение составило 0,032 рад, а максимальное смещение было менее 0,2 рад.
4.5 Оценка эффективности контроля отслеживания
Чтобы дополнительно проиллюстрировать влияние управления на боковое устойчивое состояние TTS, были проведены дополнительные эксперименты по отслеживанию и управлению на фермах по выращиванию солончаковых земель. Экспериментальные площадки включали экспериментальное поле солончаковых земель Guanxian и экспериментальную базу солончаковых земель Wudi Сельскохозяйственного университета Shandong в провинции Shandong, Китай. Дороги на солончаковых землях все сухие и утрамбованные, а используемые транспортные средства оснащены шинами с рисунком протектора повышенной проходимости, которые обеспечивают отличное трение и тягу между дорогой и шинами. Следовательно, на основе таблицы коэффициентов сопротивления качению для уравнений (15)–(18) было выбрано значение Ci = 0,035 . Как показано на рисунке 8 , в пределах фермы по выращиванию солончаковых земель было выбрано шесть экспериментальных дорог.
Чтобы гарантировать строгость эксперимента и практичность алгоритма, для сравнения были выбраны три обычных алгоритма (PID, LQR и Калмана), предлагаемый TTS-KM и TTS-DM. Как указано в Таблице 1 , для систематической оценки эффектов отслеживания и управления TTS использовались шесть показателей. Max e off представляет максимальное отклонение, mean e off - среднее отклонение, а стандартное отклонение e off представляет дискретное отклонение прицепа во время движения. Max e θ представляет максимальное отклонение угла курса; mean e θ представляет среднее отклонение угла курса; а стандартное отклонение e θ представляет колебание угла курса тягача во время движения. Эти два стандартных отклонения (стандартное отклонение e off и стандартное отклонение eθ ) могут эффективно измерить устойчивость TTS.
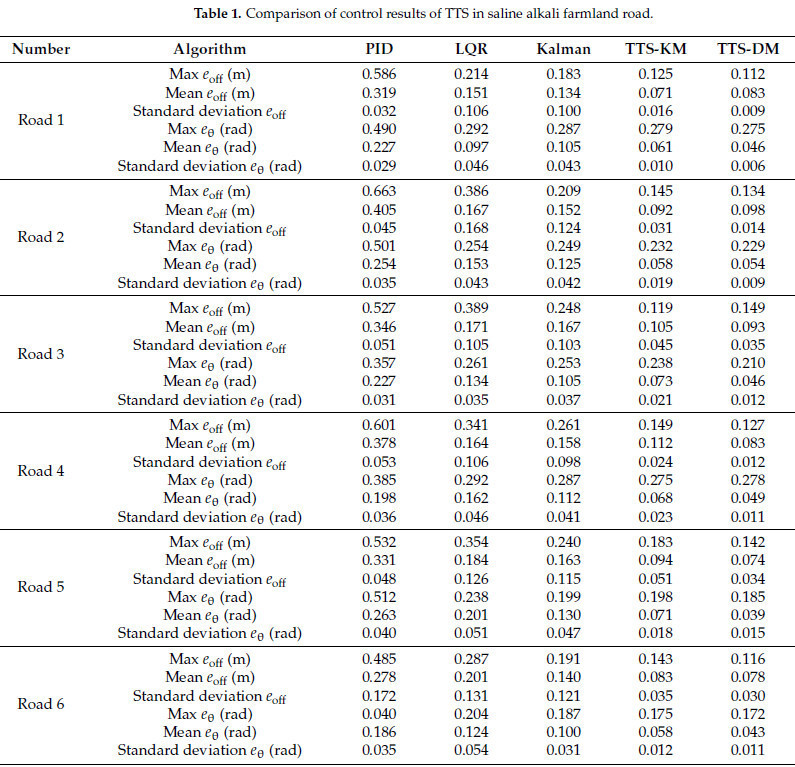
В целом, традиционные методы управления слежением, такие как ПИД, LQR и Калман, используют один путь в качестве опорной траектории для TTS. Во время эксперимента ПИД-регулятор строго придерживался заданной траектории в качестве пути слежения для прицепа. Статистические результаты показывают, что боковое отклонение и контроль устойчивости прицепа превосходят показатели, достигнутые алгоритмами LQR и Калмана. Однако эта производительность достигается за счет эффективности управления тягачом, о чем свидетельствуют самые большие значения e off и e θ среди пяти оцененных методов. Следовательно, в последующих экспериментах как регуляторы LQR, так и Калман стремились распределить траектории тягача и прицепа как можно равномернее по обе стороны от опорной траектории, чтобы достичь баланса между характеристиками управления и слежения в системе.
По сравнению с ПИД-регулятором, боковое смещение контролировалось в определённой степени; однако курсовой угол между тягачом и прицепом демонстрировал значительные колебания. Это свидетельствует о том, что тягач пошёл на значительные компромиссы в плане устойчивости управления для обеспечения эффективного отслеживания прицепа. Хотя значительные отклонения положения можно устранить с помощью регулировок, частое изменение курсовой угла может привести к неизвестным рискам. Поэтому следует избегать подобных операций при движении с высокой скоростью.
В данном исследовании, благодаря внутренним свойствам TTS, тягач и прицеп не перекрываются во время поворотов. Однако траекторию прицепа можно разумно предсказать и спланировать при определенных условиях. Два алгоритма (TTS-KM и TTS-DM) рассматривают как тягач, так и прицеп. Результаты показывают, что результаты отслеживания и управления были значительно оптимизированы и улучшены. В шести дорожных экспериментах максимальный e off системы не превышал 0,2 м, а максимальный e θ не превышал 0,28 радиан. Средний e off и средний e θ уменьшились как минимум на треть. Примечательно, что два показателя стандартного отклонения уменьшились более чем на две трети по сравнению с традиционными методами управления. Кроме того, предложенный TTS-DM немного превзошел кинематическую модель на высоких скоростях с точки зрения двух стандартных отклонений. Это говорит о том, что боковая устойчивость управления кинематической модели улучшилась, что имеет решающее значение для высокой скорости.
Фактически, даже эмпирические методы показывают, что частая и быстрая корректировка курса (эквивалентная быстрой корректировке положения рулевого колеса в реальных условиях) опасна на высоких скоростях. Следовательно, низкий уровень колебаний курса способствует безопасному вождению и стабильному управлению TTS на высоких скоростях. Экспериментальные результаты также показывают, что метод TTS-DM позволяет полностью использовать возможности авторегрессии прицепа TTS на прямых участках, избегая тем самым дополнительных и частых корректировок курса. Сравнительные эксперименты дополнительно подтверждают эффективность предлагаемого алгоритма.
5. Выводы
В данном исследовании рассматривается планирование двух траекторий и стратегия устойчивого управления системой тягача с прицепом, основанная на опыте применения интеллектуальных инженерных решений для сельскохозяйственной техники на засоленных солончаковых почвах. Традиционные исследования TTS обычно используют один путь в качестве эталона. В этом контексте несоответствие траекторий тягача и прицепа часто рассматривается как системная ошибка или ошибка управления. Фактически, результаты исследования показывают, что законы движения тягача и прицепа в TTS независимы и различны. Обеспечение согласованности траекторий активных и пассивных транспортных средств неизбежно поставит под угрозу управляемость и устойчивость системы.
Для решения задач управления устойчивостью TTS для засоленных солончаковых почв предложены алгоритм совместного прогнозирования с двойной траекторией и метод управления боковой устойчивостью, основанный на кинематической/динамической модели TTS. Во-первых, мы реконструировали кинематическую и динамическую модель TTS для удовлетворения требований применения как в условиях низкой, так и высокой скорости. Используя системную модель и анализ законов движения, мы разработали алгоритм совместного прогнозирования с двойной траекторией для генерации точных прогнозов траекторий прицепа. Таким образом, была также проверена независимость траектории между тягачом и прицепом. Впоследствии, на основе совместного прогнозирования с двойной траекторией, был предложен алгоритм управления боковой устойчивостью для TTS. Этот метод управления включает в себя стратегию градуированного управления как для условий низкой, так и для высокой скорости, а также метод управления боковой устойчивостью прицепа. Благодаря полной интеграции независимой опорной колеи прицепа с его боковым смещением схема управления оптимизирует избыточное управление, балансирует динамические характеристики слежения тягача, поддерживает неподвижность прицепа и повышает общую устойчивость управления системой.
Были проверены наблюдаемость и управляемость системы TTS с недостаточным управлением. Метод TTS-DM, основанный на стратегии управления, позволяет в полной мере использовать возможности авторегрессии прицепа на прямых участках, минимизируя тем самым необходимость частой корректировки угла курса. Этот подход решает задачу балансировки характеристик отслеживания траектории прицепа с устойчивостью динамического управления трактором, что часто является ограничением традиционных методов управления. Таким образом, он обеспечивает техническую поддержку интеллектуальной автономной навигации TTS на сложных засоленных солончаковых землях.
Предлагаемый нами метод имеет ряд ограничений: грунт должен обеспечивать достаточное сцепление для установления эффективных внешних ограничений. Слишком грязная соляная почва может изменить фрикционные свойства, поэтому может потребоваться переподбор и настройка параметров шин и коэффициента трения. Кроме того, в условиях высокой скорости точка предварительного просмотра модели водителя должна располагаться немного дальше, а бортовой компьютер должен обладать достаточной вычислительной мощностью для обеспечения производительности в режиме реального времени.
Приложение А
Представление уравнения (25) в пространстве состояний тягача с прицепом и определение матрицы параметров:
Ссылки
1. Lee, E.; Kim, T.; Mun, H.S.; Oh, J.H.; Han, S.K. Assessing the extent and severity of the impact on forest soils of two different fully mechanized timber harvesting operations. Forests 2024, 15, 985. [Google Scholar] [CrossRef]
2. Zou, L.; Liu, X.; Yuan, J.; Dong, X. Research progress in mechanized harvesting technology and equipment of leafy vegetables. J. Chin. Agric. Mech. 2022, 43, 15–23. [Google Scholar]
3. Visser, R.M.; Spinelli, R. Benefits and limitations of winch-assist technology for skidding operations. Forests 2023, 14, 296. [Google Scholar] [CrossRef]
4. Li, Y.; Zhang, P.; Yuan, J.; Liu, X. Visual positioning and harvesting path optimization of white asparagus harvesting robot. Smart Agric. 2020, 2, 65–78. [Google Scholar]
5. Chang, H.; Han, H.S.; Anderson, N.; Kim, Y.S.; Han, S.K. The cost of forest thinning operations in the western united states: A systematic literature review and new thinning cost model. J. For. 2023, 121, 193–206. [Google Scholar] [CrossRef]
6. Li, T.; Huang, S.; Niu, Z.; Hou, J.; Wu, Y.; Li, Y. Optimization and experiment of planting perpendicularity of planetary wheel garlic planter. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2020, 36, 37–45. [Google Scholar]
7. Li, J.; Liu, X.; Zou, L.; Yuan, J.; Du, S. Analysis of the interaction between end-effectors, soil and asparagus during a harvesting process based on discrete element method. Biosyst. Eng. 2020, 196, 127–144. [Google Scholar] [CrossRef]
8. Kumar, N. Backstepping based intelligent control of tractor-trailer mobile manipulators with wheel slip consideration. ISA Trans. 2024, 153, 78–95. [Google Scholar]
9. Shi, M.; Feng, X.; Pan, S.; Song, X.; Jiang, L. A collaborative path planning method for intelligent agricultural machinery based on unmanned aerial vehicles. Electronics 2023, 12, 3232. [Google Scholar] [CrossRef]
10. Tang, Y.; Cai, Y.; Liu, Z.; Sun, X.; Chen, L.; Wang, H.; Dong, Z. Research on active trailer steering control strategy of tractor semitrailer under medium-/high-speed conditions. Actuators 2024, 13, 360. [Google Scholar] [CrossRef]
11. Ren, H.; Wu, J.; Lin, T.; Yao, Y.; Liu, C. Correction: Ren et al. Research on an Intelligent Agricultural Machinery Unmanned Driving System. Agriculture 2023, 13, 1907. Agriculture 2024, 14, 13. [Google Scholar]
12. Wang, P.; Yue, M.; Yang, L.; Luo, X.; He, J.; Man, Z.; Feng, D.; Liu, S.; Liang, C.; Deng, Y.; et al. Design and test of intelligent farm machinery operation control platform for unmanned farms. Agronomy 2024, 14, 804. [Google Scholar] [CrossRef]
13. Murillo, M.; Sánchez, G.; Deniz, N.; Genzelis, L.; Giovanini, L. Improving path-tracking performance of an articulated tractor-trailer system using a non-linear kinematic model. Comput. Electron. Agric. 2022, 196, 106826. [Google Scholar] [CrossRef]
14. Wen, H.; Ma, X.; Qin, C.; Chen, H.; Kang, H. Research on path tracking of unmanned spray based on dual control strategy. Agriculture 2024, 14, 562. [Google Scholar] [CrossRef]
15. Ahn, Y.; Han, S.; Kim, G.; Huh, K. Slope and mass estimation for semi-trailer tractor considering pitch angle variations. IEEE Trans. Intell. Veh. 2024, 1, 1–13. [Google Scholar] [CrossRef]
16. Zhou, Y.; Chung, K.W. Path tracking control of a tractor-trailer wheeled system kinematics with a passive steering angle. Appl. Math. Model. 2022, 109, 341–357. [Google Scholar] [CrossRef]
17. Jin, Z.; Wang, C.; Liang, D.; Wang, S.; Ding, Z. Fixed-time consensus for multiple tractor-trailer vehicles with dynamics control: A distributed internal model approach. IEEE Trans. Intell. Veh. 2024, 9, 656–669. [Google Scholar] [CrossRef]
18. Wang, D.; Moon, I.; Zhang, R. Multi-trip multi-trailer drop-and-pull container drayage problem. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19088–19104. [Google Scholar] [CrossRef]
19. Jin, X.; Liang, J.; Dai, S.L.; Guo, D. Adaptive line-of-sight tracking control for a tractor-trailer vehicle system with multiple constraints. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11349–11360. [Google Scholar] [CrossRef]
20. Han, S.; Yoon, K.; Park, G.; Huh, K. Hybrid state observer design for estimating the hitch angles of tractor-multi unit trailer. IEEE Trans. Intell. Veh. 2023, 8, 1449–1458. [Google Scholar] [CrossRef]
21. Zhao, C.; Zhu, Y.; Du, Y.; Liao, F.; Chan, C.Y. A novel direct trajectory planning approach based on generative adversarial networks and rapidly-exploring random tree. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17910–17921. [Google Scholar] [CrossRef]
22. Han, S.; Yoon, K.; Park, G.; Huh, K. Robust lane keeping control for tractor with multi-unit trailer under parametric uncertainty. IEEE Trans. Intell. Veh. 2024, 9, 2333–2347. [Google Scholar] [CrossRef]
23. Chen, K.; Deng, J.; Zhang, W.Z. Kinematic analysis of tractor-trailer mobile robot on a sphere. In Proceedings of the 2023 International Conference on Intelligent Communication and Computer Engineering (ICICCE), Changsha, China, 27–29 December 2023; pp. 121–128. [Google Scholar]
24. Shojaei, K.; Taghavifar, H. Input-output feedback linearization control of a tractor with n-trailers mechanism considering the path curvature. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 9700–9715. [Google Scholar] [CrossRef]
25. Yun, S.H.; Yang, J.G.; Huh, K.S. Development of a narrow passage driving system for semi-trailer tractor by using MPC. Int. J. Automot. Technol. 2022, 23, 785–791. [Google Scholar] [CrossRef]
26. DeSantis, R.M. Path-tracking for a tractor-trailer-like robot. Int. J. Robot. Res. 1994, 13, 533–544. [Google Scholar] [CrossRef]
27. Bulgakov, V.; Aboltins, A.; Ivanovs, S.; Beloev, H.; Nadykto, V.; Ihnatiev, Y.; Olt, J. Theory of movement of machine-tractor unit with trailer haulm harvester machine. Appl. Sci. 2022, 12, 3901. [Google Scholar] [CrossRef]
28. Hellander, A.; Bergman, K.; Axehill, D. On Integrated optimal task and motion planning for a tractor-trailer rearrangement problem. In Proceedings of the 2023 62nd IEEE Conference on Decision and Control (CDC), Singapore, 13–15 December 2023; pp. 6116–6123. [Google Scholar]
29. Zhao, H.; Chen, W.; Zhou, S.; Zheng, F.; Liu, Y.H. Localization and motion planning of industrial tractor–trailers vehicles. IEEE Trans. Control Syst. Technol. 2023, 31, 2928–2936. [Google Scholar] [CrossRef]
30. Lu, E.; Zhao, X.; Ma, Z.; Xu, L.; Liu, Y. Robust leader-follower control for cooperative harvesting operation of a tractor-trailer and a combine harvester considering confined space. IEEE Trans. Intell. Transp. Syst. 2024, 25, 17689–17701. [Google Scholar] [CrossRef]
31. Liu, J.; Han, W.; Peng, H.; Wang, X. Trajectory planning and tracking control for towed carrier aircraft system. Aerosp. Sci. Technol. 2019, 84, 830–838. [Google Scholar] [CrossRef]
32. Ruan, X.; Huang, Y.; Wang, Y.; Fu, Z.; Xiong, L.; Yu, Z. An efficient trajectory-planning method with a reconfigurable model for any tractor trailer vehicle. IEEE Trans. Transp. Electrif. 2023, 9, 3360–3374. [Google Scholar] [CrossRef]
33. Jin, X.; Dai, S.L.; Liang, J. Adaptive constrained formation-tracking control for a tractor-trailer mobile robot team with multiple constraints. IEEE Trans. Autom. Control 2023, 68, 1700–1707. [Google Scholar] [CrossRef]
34. Manav, A.C.; Lazoglu, I.; Aydemir, E. Adaptive path following control for autonomous semi-trailer docking. IEEE Trans. Veh. Technol. 2022, 71, 69–85. [Google Scholar] [CrossRef]
35. Widyotriatmo, A.; Nazaruddin, Y.Y.; Putrantob, M.R.F.; Ardhi, R. Forward and backward motions path following controls of a tractor-trailer with references on the head-tractor and on the trailer. ISA Trans. 2020, 105, 349–366. [Google Scholar] [CrossRef]
36. Ljungqvist, O.; Evestedt, N.; Axehill, D.; Cirillo, M.; Pettersson, H. A path planning and path following control framework for a general 2-trailer with a car-like tractor. J. Field Robot. 2019, 36, 1345–1377. [Google Scholar] [CrossRef]
37. Peng, H.; Shi, B.; Song, J.; Wang, X. A symplectic method for trajectory planning of general tractor-trailer systems. Appl. Math. Model. 2023, 114, 205–229. [Google Scholar] [CrossRef]
38. Ito, N.; Okuda, H.; Suzuki, T. Configuration-aware model predictive motion planning for Tractor–Trailer Mobile Robot. Adv. Robot. 2023, 37, 329–343. [Google Scholar] [CrossRef]
39. Lei, G.; Zheng, Y. Research on collaborative trajectory planning algorithm based on Tractor-Trailer Wheeled System. IEEE Access 2022, 10, 64209–64221. [Google Scholar] [CrossRef]
40. Zhuang, J. Automotive Tire Science, 1st ed.; Beijing Institute of Technology Press: Beijing, China, 1995; pp. 186–229. [Google Scholar]
Lei G, Zhou S, Zhang P, Xie F, Gao Z, Shuang L, Xue Y, Fan E, Xin Z. Stability Control of the Agricultural Tractor-Trailer System in Saline Alkali Land: A Collaborative Trajectory Planning Approach. Agriculture. 2025; 15(1):100.
Перевод статьи «Stability Control of the Agricultural Tractor-Trailer System in Saline Alkali Land: A Collaborative Trajectory Planning Approach» авторов Lei G, Zhou S, Zhang P, Xie F, Gao Z, Shuang L, Xue Y, Fan E, Xin Z., оригинал доступен по ссылке. Лицензия: CC BY. Изменения: переведено на русский язык
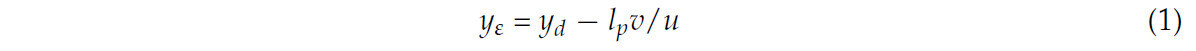
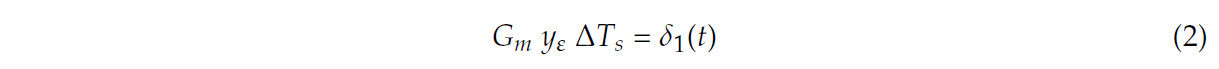
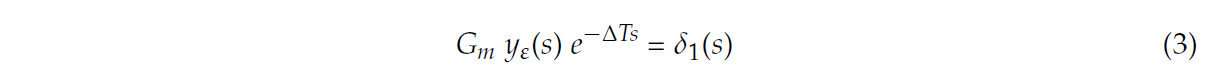
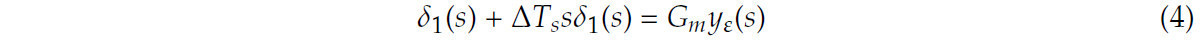
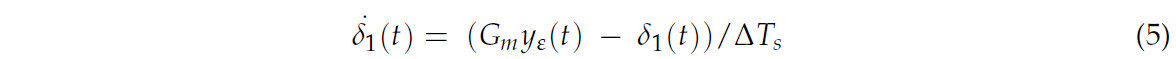
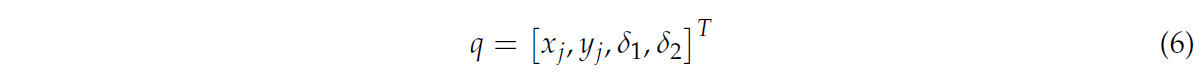
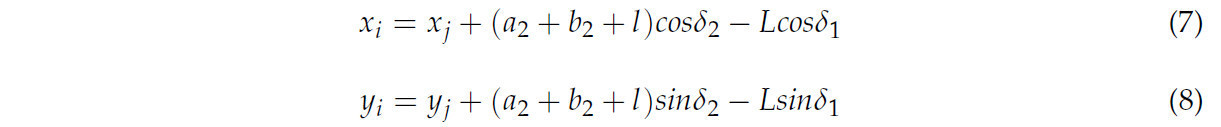
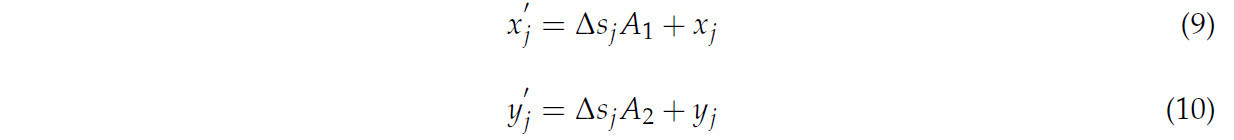
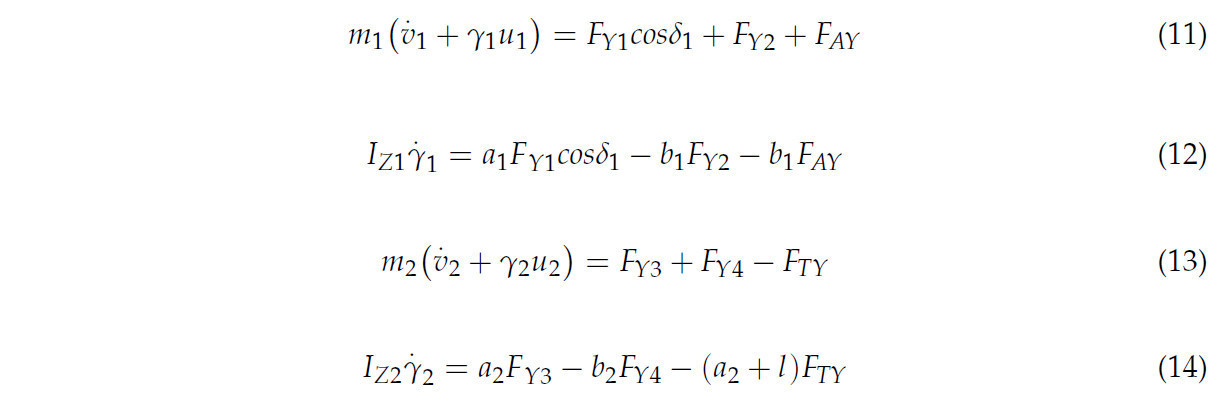
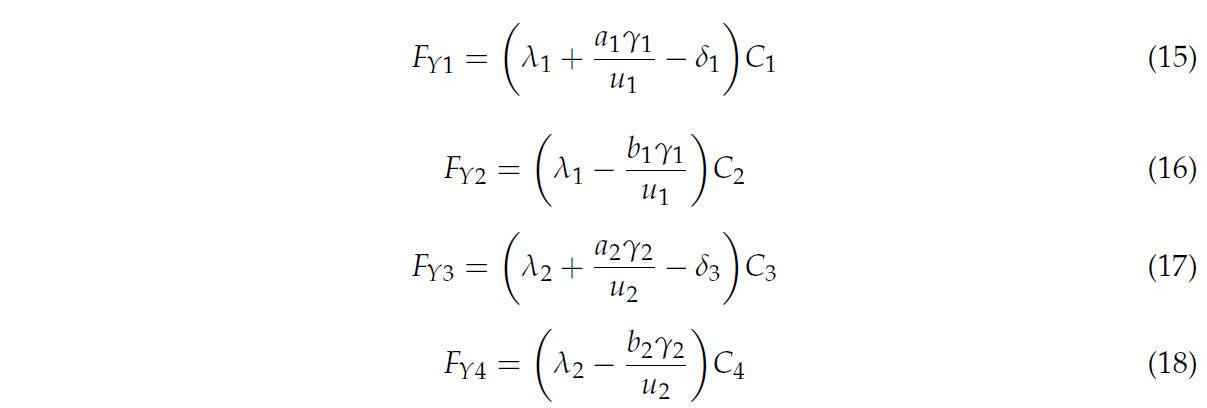
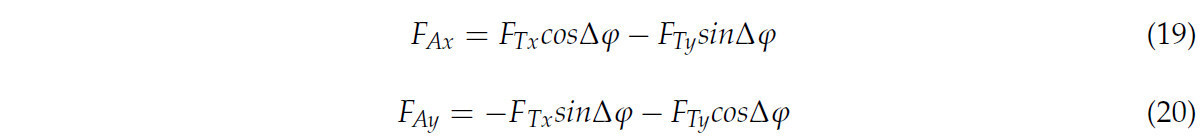
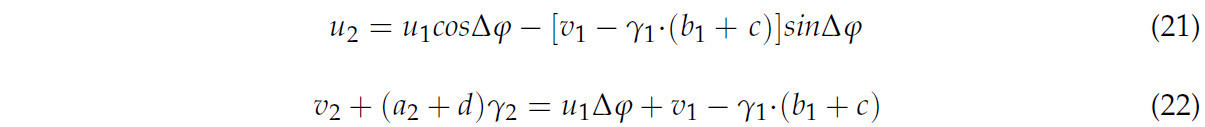
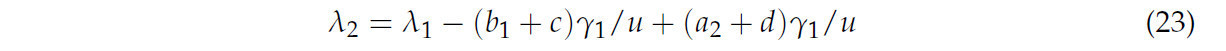
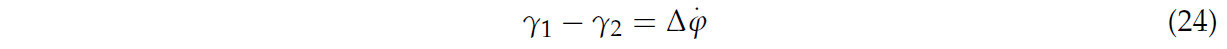
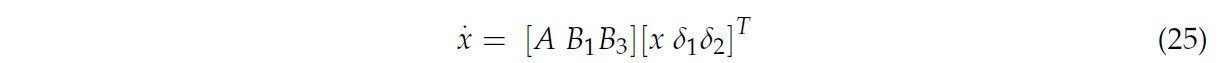
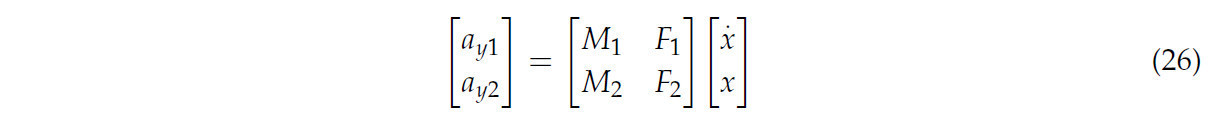
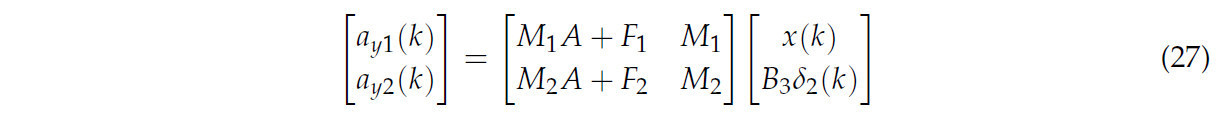
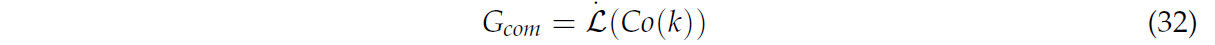
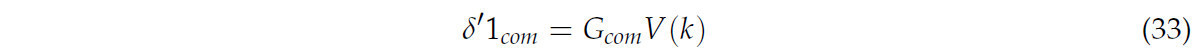
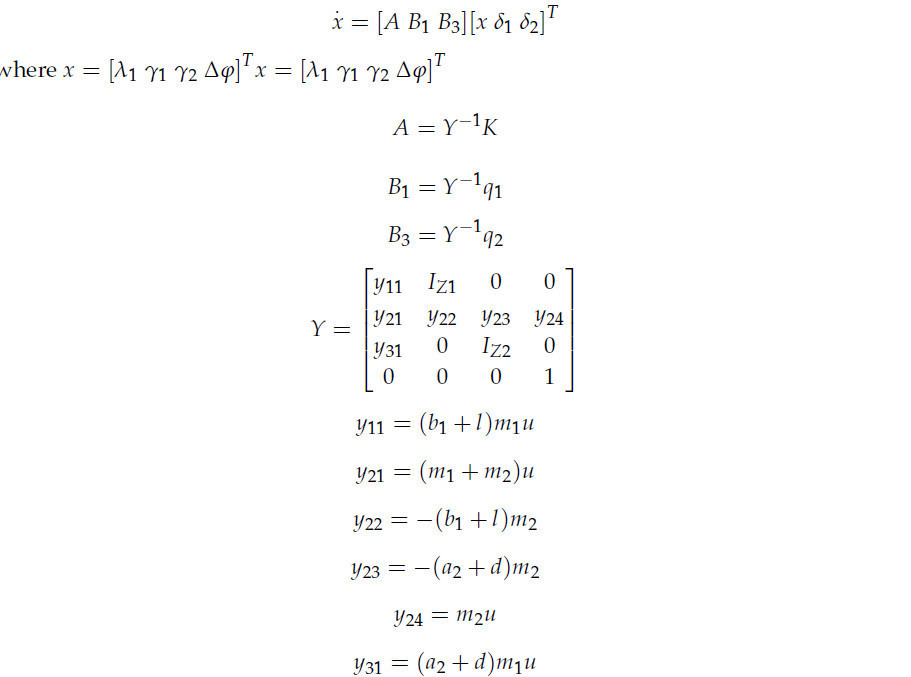

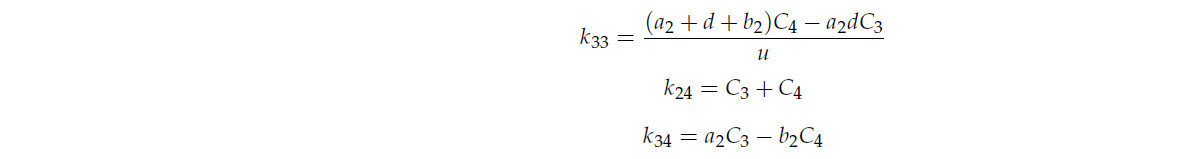
































































































Комментарии (0)