Генотипическая идентификация кукурузы на основе трехмерного структурного фенотипирования и гауссовского нечеткого кластерного анализа

Метелка кукурузы – один из важнейших органов, определяющих урожайность и качество кукурузы. Изучение её фенотипической информации – чрезвычайно важная задача в селекционной работе, поскольку оптимальная структура метёлки имеет основополагающее значение для достижения высокой урожайности кукурузы. Высокопроизводительные технологии фенотипирования предоставляют важные инструменты для повышения эффективности анализа фенотипической информации о метелках кукурузы. 

С этой целью мы разработали полностью автоматизированный многоракурсный цифровой аппарат для получения изображений, предназначенный для метелок кукурузы. Это устройство использовалось для получения изображений метёлок 1227 инбредных линий кукурузы, относящихся к трём генотипическим классификациям (NSS, TST и SS). Используя алгоритм трёхмерной реконструкции SFM (Structure from Motion – Структура из движения), мы быстро получили облака точек метёлок кукурузы. Затем мы использовали алгоритм TreeQSM, специально разработанный для извлечения топологических структур деревьев, для извлечения 11 архетипических структурных фенотипических параметров метелок кукурузы. К ним относятся диаметр главного колоса, высота короны, длина главного колоса, длина стебля, диаметр стебля, количество ветвей, общая длина ветвей, средний диаметр короны, максимальный диаметр короны, объём выпуклой оболочки и площадь короны. Наконец, мы сравнили алгоритм нечёткой гауссовой кластеризации (GFC), использованный в данном исследовании, с общепринятыми алгоритмами, такими как RF (случайный лес), SVM (машина опорных векторов) и BPNN (нейронная сеть BP), а также k-средними, HCM (иерархический) и FCM (нечёткие C-средние). Затем мы провели корреляционный анализ между извлечёнными фенотипическими параметрами структуры метелки кукурузы и генотипами материалов кукурузы. Результаты исследования показали, что алгоритм нечёткой гауссовой кластеризации является оптимальным выбором для кластеризации генотипов кукурузы. В частности, точность классификации для генотипа «Нежёсткий стебель» (NSS) и генотипа «Тропический и субтропический» (TST) достигла 67,7% и 78,5% соответственно. Более того, среди образцов кукурузы с различными генотипами наибольшей изменчивостью характеризовались такие показатели, как количество ветвей, общая длина ветвей и длина главного колоса, а наименьшей – объём кроны, средний диаметр кроны и площадь кроны. Это не только послужило важной отправной точкой для углубленного изучения изменчивости фенотипических параметров метёлок кукурузы, но и открыло новый подход к скринингу селекционного материала.

Кукуруза — одна из важнейших продовольственных культур в мире, и её урожайность критически важна для обеспечения продовольственной безопасности [ 1 ]. Генетические методы селекции могут помочь повысить урожайность кукурузы и обеспечить глобальную продовольственную безопасность. Ускоренная локализация функциональных генов с помощью высокопроизводительных методов получения фенотипической информации пользуется огромным спросом на рынке [ 2 ] и является ключом к созданию улучшенных сортов [ 3 ].

Исследования показали, что структура метелок кукурузы напрямую связана с урожайностью пыльцы и эффективностью опыления, что влияет не только на конечный урожай зерна, но и на сохранение инбредной линии [ 4 ]. Однако слишком густое ветвление мужской метелки и слишком большой размер мужской метелки не способствуют конечному урожаю кукурузы. Напротив, с одной стороны, это снизит эффективность фотосинтеза листьев из-за слишком большой площади затенения, а с другой стороны, это будет потреблять большое количество питательных веществ, влияя на формирование и округлость зерен [ 5 , 6 ]. Нахождение правильной структуры метелок кукурузы важно для селекции хороших сортов кукурузы. В последние годы технологии высокопроизводительного фенотипирования сыграли важную роль в селекционной работе многих сельскохозяйственных культур, и все больше и больше генов, связанных с фенотипическими признаками метелки кукурузы, были успешно обнаружены [7]. Технологии высокопроизводительного фенотипирования сыграли решающую роль в селекции сельскохозяйственных культур. В сочетании с технологией GWAS удалось успешно локализовать больше генов, связанных с такими признаками метелки кукурузы, как длина метелки, длина ветвей, количество ветвей, диаметр стебля, диаметр главного колоса и длина стебля, которые можно легко, недорого и точно количественно оценить. Это сделало структуру метелки кукурузы удобным объектом для изучения QTL [8, 9] и важной основой для быстрого скрининга превосходных признаков метелки [10, 11].

Однако при высокопроизводительных фенотипических измерениях метелок кукурузы, множество параметров характеристики и короткий период опыления, в течение которого метелки перестают расти и начинают деградировать, делают эффективное время, доступное для измерения структурных признаков метелок, весьма ограниченным. Кроме того, метелки кукурузы очень легко дегидратируются после отделения от растения, в результате чего метелки легко ломаются и даже претерпевают значительные морфологические изменения, что крайне неблагоприятно для получения высокопроизводительных данных о метелках кукурузы. Кроме того, такие показатели, как максимальный диаметр коронки, высота коронки, средний диаметр коронки и ширина коронки, также трудно измерить вручную. Поэтому особенно важно разработать высокопроизводительные методы измерения метелки кукурузы.

В настоящее время для извлечения фенотипов сельскохозяйственных культур используется большое количество методов, основанных на изображениях и облаках точек, например, использование изображений для извлечения трехмерной структуры проростков кукурузы [ 12 ] и извлечения площади листьев и высоты растения кукурузы [ 13 , 14 , 15 ], а также извлечения количества ветвей, длины ветвей и угла метелки [ 16 , 17 ], и для этой цели также были разработаны системы [ 18 , 19 , 20 ]. Однако для анализа трехмерных структурных параметров двумерные изображения не могут преодолеть проблему окклюзии. Трехмерные данные облаков точек предлагают значительные преимущества при извлечении нескольких структурных параметров целевого объекта [ 21 , 22 , 23 ]. В настоящее время большинство данных облаков точек генерируются с помощью трехмерных сканирующих устройств, таких как LiDAR (2D/3D), TOF-камеры (камеры времени пролета) и сканеры структурированного света. Наземное лазерное сканирование (TLS) может точно характеризовать 3D-структуру деревьев с точностью до миллиметра [ 24 , 25 ]. Лей и Суреш и др. [ 26 ] использовали данные наземного LiDAR для извлечения 3D-структурной информации о растениях кукурузы, включая площадь листьев и угол наклона листьев. Паулус и др. [ 27 ] изучали получение и реконструкцию 3D-облака точек ячменя с использованием LiDAR с измерительным рычагом для извлечения площади листьев и высоты растений. Чайвиватракул и др. [ 28 ] использовали камеру TOF для получения данных об облаке точек проростков кукурузы для реконструкции 3D-модели проростков кукурузы, извлекая такую ​​информацию, как максимальный/минимальный диаметр стебля, высота стебля, площадь листьев, длина листьев и угол наклона листьев. Однако этим методам часто не хватает плотности облака точек или геометрической точности при изучении объектов в масштабе органа, таких как метелка кукурузы. Донг и Шэн и др. [ 4 , 29 ] построили трёхмерное облако точек метёлки кукурузы, используя изображения и извлечённые показатели, такие как высота растения, площадь листа, длина главного колоса и количество ветвей. Однако существуют проблемы, связанные с низкой автоматизацией, высокой стоимостью и низкой эффективностью анализа. Сюй и др. [ 30] сделали значительный шаг вперед. Они разработали систему, известную как TIPS (система трехмерного фенотипирования изображений). Эта система использует алгоритм TreeQSM. С помощью этого алгоритма она реконструирует и анализирует топологию отдельного дерева. Таким образом, ей удается извлечь фенотипические параметры структуры метелки кукурузы, имеющие сходство со структурой дерева. Этот процесс извлечения предлагает несколько решений. Он решает проблему автоматического получения изображений метелки кукурузы. Он также решает проблемы, связанные с созданием трехмерного облака точек и реконструкцией топологии метелки. Более того, система дополнительно оценивает некоторые аспекты. Она изучает пространственную изменчивость облака точек. Она также оценивает извлеченные длины осевых веретен метелки. Кроме того, она анализирует количество ветвей, общую длину ветвей и углы наклона ветвей. Оценка приводит к выводу. Результаты показывают, что система эффективна и точна. С другой стороны, система выполняет определенную задачу. Это решает проблему инструмента для извлечения фенотипических параметров метелок кукурузы. Однако есть и недостаток: не проводилось анализа генетической связи между фенотипом и генотипированием.

Генотипы кластеризации метелки с использованием фенотипических параметров метелки эффективны и просты в использовании, и они являются инновационным аспектом этого исследования. Поскольку структурные фенотипы метелки кукурузы в значительной степени контролируются генотипами, разные генотипы демонстрируют значительные различия в морфологии метелки, что обеспечивает возможность анализа структурной фенотипической информации метелки для изучения различий в фенотипических характеристиках среди четырех генотипов кукурузы. Сонг и др. [ 31 ] получили разные категории генов после кластеризации разных функциональных генов с помощью алгоритма GFC, показывающего характеристики распределения данных об экспрессии генов в пространстве кластеризации. Минтон и др. [ 32 ] предоставили пошаговое руководство для проведения морфометрического анализа растений с использованием модели гауссовой смеси и создали новую концептуальную, статистическую и вероятностную структуру для анализа морфометрических данных в таксономии растений. Янг и др. [ 33 ] расширили модельно-ориентированный метод гауссовой кластеризации на нечеткую модель и предложили неконтролируемый алгоритм гауссовой кластеризации, основанный на нечеткой модели, который решил проблемы традиционного алгоритма гауссовой кластеризации, чувствительного к инициализации и требующего предварительного указания количества кластеров. Фукс и др. [ 34 ] сравнили модель гауссовой смеси с существующими передовыми моделями кластеризации смешанных данных на нескольких часто используемых наборах данных. Результаты показали, что эта модель может достигать более точных и стабильных результатов кластеризации при работе со смешанными данными и превосходит традиционные методы кластеризации. Янг и др. [ 35 ] использовали набор для анализа GoldenGate (Illumina, Сан-Диего, Калифорния, США), содержащий 1536 SNP и подход картирования ассоциаций для 12 фенотипических признаков, чтобы типизировать 527 линий и исследовать взаимосвязь между генотипической и фенотипической дисперсией. Была исследована связь между генотипами и фенотипическими вариантами. Пан и др. [ 36 ] использовали иерархическую кластеризацию для кластеризации фенотипических параметров 24 ресурсов зародышевой плазмы арбуза, выявив их разнообразие и закономерности вариации. Сье и др. [ 37 ] использовали изображения RGB с БПЛА для кластеризации восьми фенотипических параметров 300 сортов рапса во время цветения, используя динамический метод K-средних, сгруппировав сорта рапса в четыре категории на основе характеристик цветения. Хан и др. [ 38 ] изучали фенотипическую изменчивость среди различных генотипов, используя динамические изменения высоты растений кукурузы, и анализировали генотипы кукурузы, используя GFC (гауссовскую нечеткую кластеризацию). Ринкон, Мустафа и Шреста и др. [ 39 , 40][] провели кластерный анализ образцов кукурузы на основе множественных фенотипических признаков, таких как высота растения, длина и ширина листа, температура листа, плотность корней и вес, для изучения изменчивости признаков у различных образцов кукурузы. Однако исследования кластеризации генотипов с использованием фенотипических параметров метелки ограничены.

Существующие результаты исследований решили проблемы получения многоракурсных изображений, 3D-синтеза, топологической реконструкции и автоматического извлечения фенотипических параметров, таких как длина главного колоса кукурузы, количество ветвей, длина ветвей и угол ветвления [ 30 ]. На этой основе в этом исследовании дополнительно извлекли семь фенотипических параметров, таких как диаметр главного колоса, высота короны, диаметр стебля, средний диаметр короны, максимальный диаметр короны, объем короны и площадь короны из 1227 метелок кукурузы. Кроме того, после шумоподавления исходных данных облака точек с использованием алгоритмов гауссовой фильтрации и DBSCAN (Density-Based Spatial Clustering of Applications with Noise) были успешно извлечены 1227 облаков точек метелок кукурузы отдельных растений. Наконец, был проведен генотипический кластерный анализ этих 1227 данных облака точек метелок кукурузы отдельных растений с использованием алгоритма гауссовой нечеткой кластеризации (GFC). Результаты кластеризации показали, что метод этого исследования оказал относительно хороший эффект классификации на нежестком стебле (NSS) и тропических и субтропических (TST) материалах. Метод смог выявить изменчивость множественных структурных фенотипических параметров метелки кукурузы. Кроме того, по сравнению с традиционными широко используемыми алгоритмами машинного обучения, алгоритм кластеризации, принятый в этом исследовании, имел более высокую точность классификации. Это исследование инновационно использовало трехмерный структурный фенотип метелки кукурузы для кластеризации генотипов кукурузы, обеспечивая определенное эталонное значение для скрининга материалов в процессе селекции кукурузы. Наконец, после сравнения измеренных данных это исследование показало, что, хотя точность кластеризации измеренных данных увеличилась на 5% до 10%, метод, принятый в этом исследовании, был более эффективным, более экономичным и более практичным.

2.1. Область исследования и данные ручных измерений метелки

Район исследования расположен в Национальной базе исследований и демонстраций точного земледелия в Сяотаншане, округ Чанпин, Пекин (40°10′60″ с. ш., 116°26′30″ в. д.). В 2022 году мы собрали в общей сложности 409 образцов, в результате чего было получено 1227 изображений метелок кукурузы после опыления (каждый образец состоит из трех наборов изображений, по 72 изображения в каждом наборе). Каждый образец был высажен в два ряда с междурядьем 0,6 м и расстоянием между растениями 0,4 м. Генотипические типы этих 409 наборов материалов кукурузы были основаны на результатах, проанализированных программой Bayesian Markov Chain Monte Carlo (BMCMC) с использованием программного обеспечения STRUCTURE (версия 2.3.4) [ 41 , 42 ]. Эти результаты классифицировали генотипы материалов кукурузы в общей сложности на четыре подгруппы: Тропические и субтропические (TST) ресурсы зародышевой плазмы кукурузы адаптированы к тропическому и субтропическому климату, обладая основными признаками, которые позволяют им хорошо расти в жарких и влажных условиях, и этот генотип ресурсов зародышевой плазмы обладает сильной засухоустойчивостью. Ресурсы зародышевой плазмы кукурузы с нежестким стеблем (NSS) и жестким стеблем (SS) - это способ, которым доктор Дювик из Pioneer в США классифицирует гибриды кукурузы в соответствии с различными требованиями родителя и матери. NSS классифицируется как реплика, которая характеризуется небольшой пыльцевой нагрузкой и коротким временем рассеивания пыльцы, в то время как SS классифицируется как родитель, который характеризуется высокой урожайностью семян. Среди них было 28 генотипов SS, 175 генотипов NSS и 140 генотипов TST. Остальные 55 образцов имели вероятности генотипирования ниже 0,60 и были классифицированы как смешанные субпопуляции (MIXED).

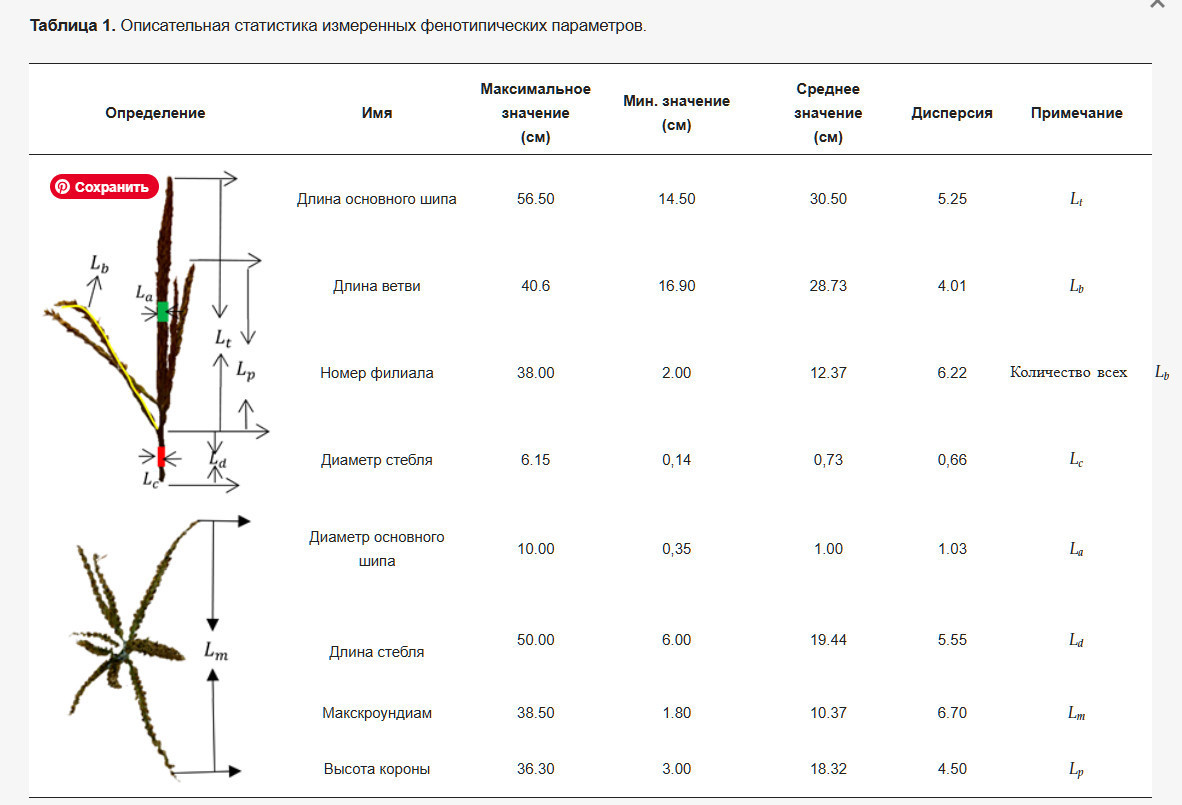
Измеренные данные в этом исследовании включали длину главного колоса, длину ветки, количество ветвей, диаметр колоса, диаметр стебля, длину стебля, диаметр коронки и высоту коронки метелки. Длина стебля относится к части от самого нижнего цветочного шёлка на главном стебле метелки до первого узла на верхушке стебля кукурузы. Maxcrowndiam и crown height относятся к максимальному диаметру коронки и максимальной высоте коронки, соответственно. Подробная диаграмма измерений фенотипических параметров представлена ​​в Таблице 1. Все длины измеряли в выпрямленном состоянии с использованием линейки с разрешением 1 мм. Диаметр La представляет собой среднее значение диаметров пяти равноудаленных областей на главном колосе, в то время как Ld относится к длине от начальной точки первой ветви метелки до самого высокого узла растения кукурузы под метелкой. Его диаметр Lc также является средним значением пяти равноудаленных диаметров.

2.2. Разработка TIPS и получение изображений

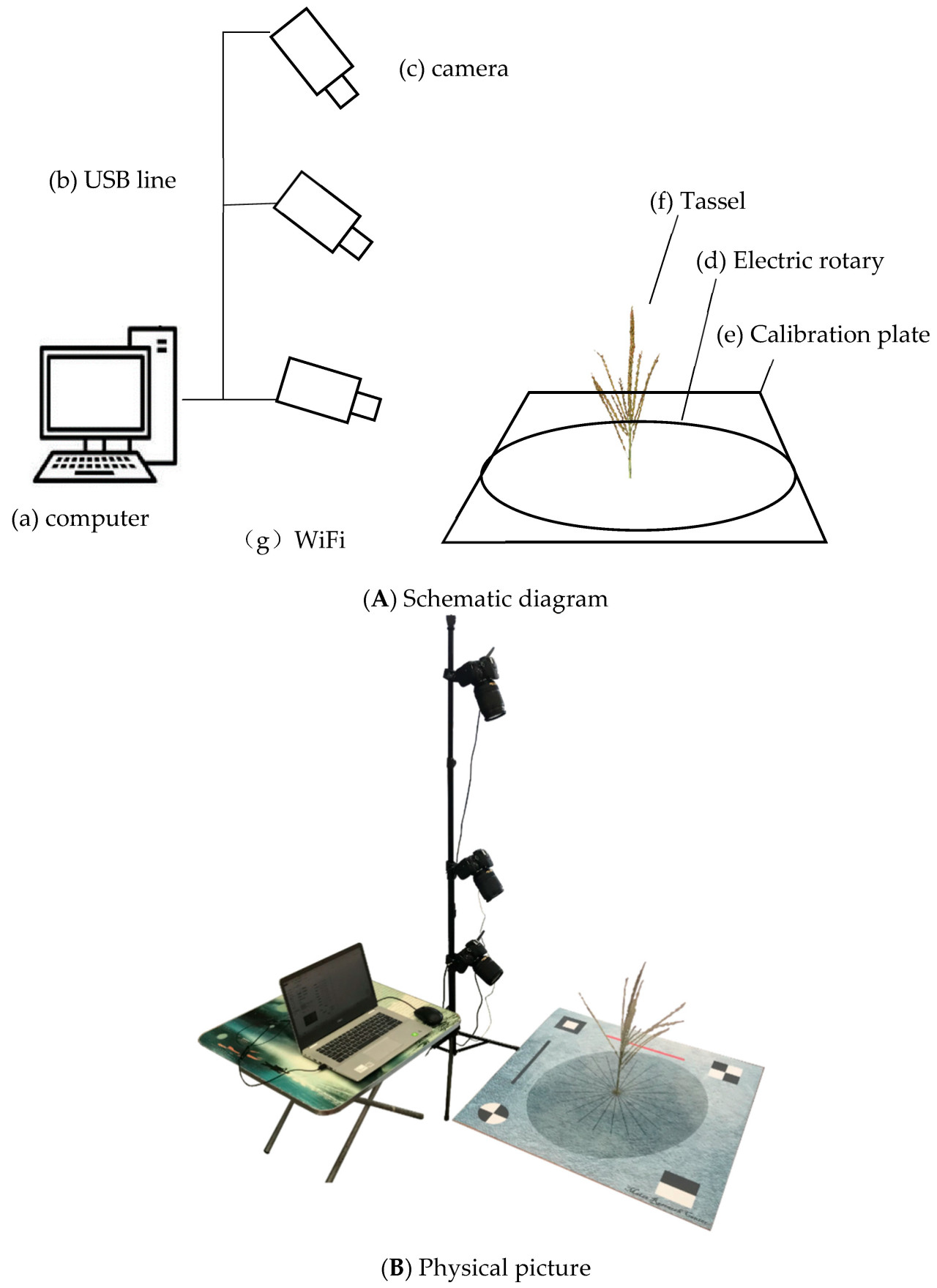
Получение изображений в основном автоматизировано с помощью системы TIPS, состоящей из четырёх основных компонентов: аппаратного обеспечения, системы передачи данных, системы сбора данных и обработки данных. Аппаратное обеспечение включает в себя электрический поворотный стол, эталонную плату, три цифровые камеры и компьютер. Модуль передачи данных включает в себя беспроводную связь Wi-Fi для электрического поворотного стола и проводное соединение RS232-USB для камер. Модуль сбора данных включает в себя настройку параметров, предварительный просмотр изображений, управление съёмкой, а также классификацию и хранение данных. Модуль обработки включает в себя трёхмерную реконструкцию облака точек на основе последовательностей изображений, калибровку облака точек, сегментацию облака точек и извлечение фенотипической информации.

Используя аппаратный модуль системы TIPS, а также передачу, сбор и обработку данных, мы получили 360-градусные изображения метелки кукурузы. Для каждой метелки было сделано 72 снимка, охватывающих верхнюю, среднюю и нижнюю части. Использовалась цифровая камера Nikon D5600 с эффективным разрешением 24,16 мегапикселей и объективом Nikon 18–140 мм f/3.5–5.6 G ED VR с 7-кратным зумом. Для съёмки камера была установлена ​​в режим фиксированного фокусного расстояния. Электрический поворотный стол, управляемый по беспроводному Wi-Fi с точностью 0,01 градуса, имеет диаметр 60 см и питается от источника постоянного тока напряжением 24 В. Калибровочная плата представляет собой квадрат со стороной 80 см.

Процессы сбора и хранения данных выполнялись автоматически с помощью программного обеспечения для управления сбором данных, разработанного на языке C# на платформе Visual Studio 2010. На рисунке 1 представлены структурная и физическая схемы системы TIPS.

Во время измерения кисточка фиксируется в центре калибровочной доски. Цифровые камеры и штатив фиксируются, а фокусное расстояние регулируется таким образом, чтобы калибровочная доска занимала более 70% поля зрения. При этом перекрытие изображений кисточки в верхней, средней и нижней частях также должно составлять не менее 70%.

Затем активируется программное обеспечение для сбора данных, которое задаёт высоту и интервалы между съёмками для трёх камер, после чего автоматически собирает данные о 360-градусном изображении кисточки. Всего было получено 1227 эффективных изображений кисточки, что в сумме составляет 88 344 изображения. Весь процесс занял 81,8 часа.

2.3. Создание облака точек и предварительная обработка

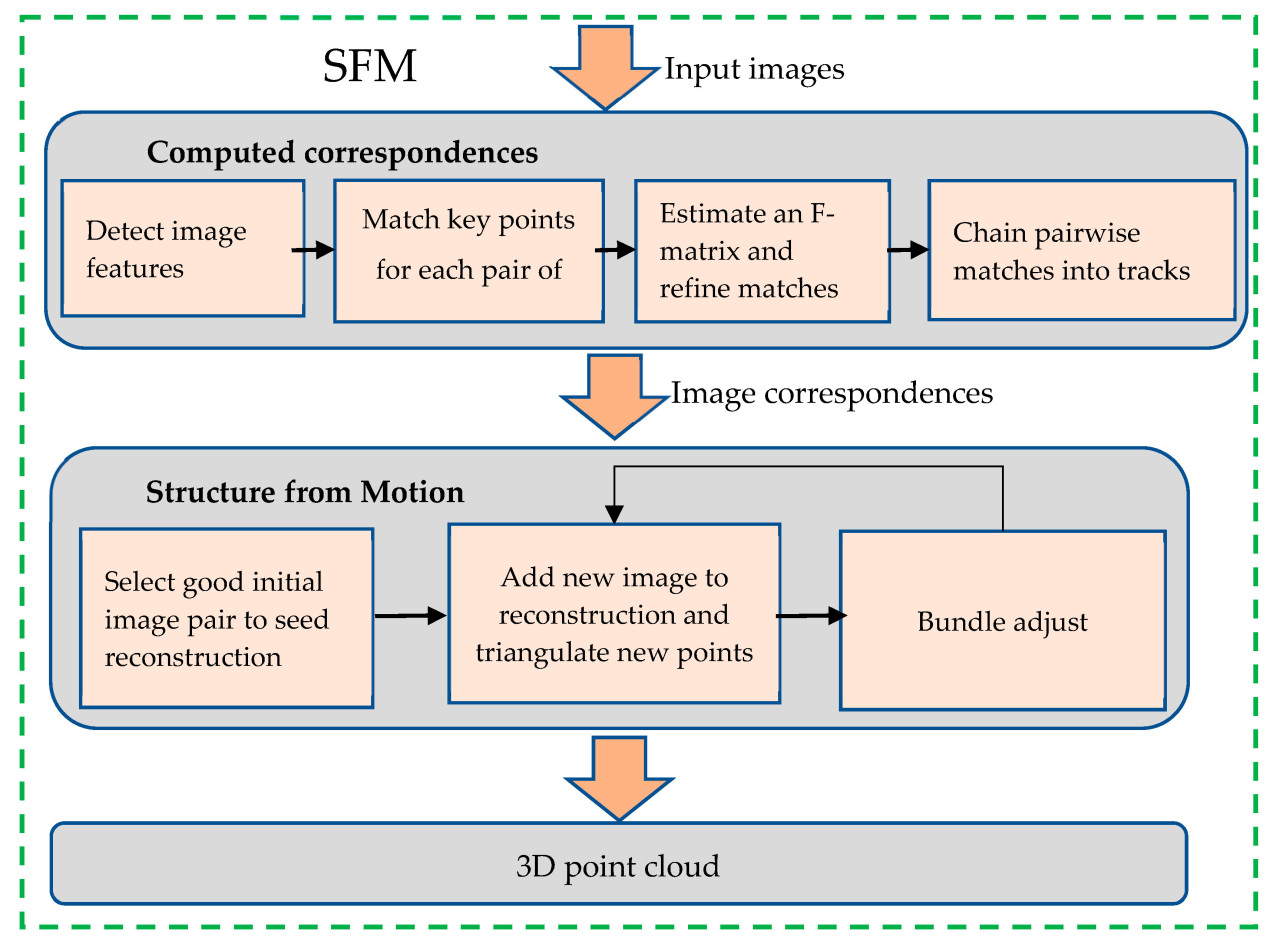
После получения изображения необходимо провести трёхмерную реконструкцию облака точек с помощью алгоритма SFM (структура из движения). Как показано на рисунке 2. Процесс использования алгоритма SFM для создания трёхмерного облака точек метёлки кукурузы выглядит следующим образом. Сначала алгоритм SFM извлекает информацию о фокусном расстоянии из входных изображений. Затем для извлечения признаков изображения применяются алгоритмы извлечения признаков, такие как SIFT. Затем модель kd-tree используется для вычисления евклидова расстояния между характерными точками двух изображений для выполнения сопоставления характерных точек с целью определения пар изображений с необходимым количеством совпадений характерных точек.

Для каждой из этих пар сопоставленных изображений вычисляется эпиполярная геометрия, а матрица F оценивается и оптимизируется с помощью алгоритма RANSAC для повышения качества сопоставления пар. Если в паре сопоставления удаётся обнаружить и сопоставить характерную точку, и она непрерывно обнаруживается, будет сформирована траектория точки сопоставления.

Затем новые изображения включаются в цикл SFM для корректировки пучка. Этот процесс продолжается до тех пор, пока не останется подходящих изображений для добавления. Наконец, в данном исследовании для создания трёхмерного облака точек метёлки кукурузы была применена корректировка разреженного пучка.

Этот алгоритм подходит для различных типов сцен и объектов, будь то внутренние или внешние, статические объекты или динамические сцены [ 43 , 44 ].

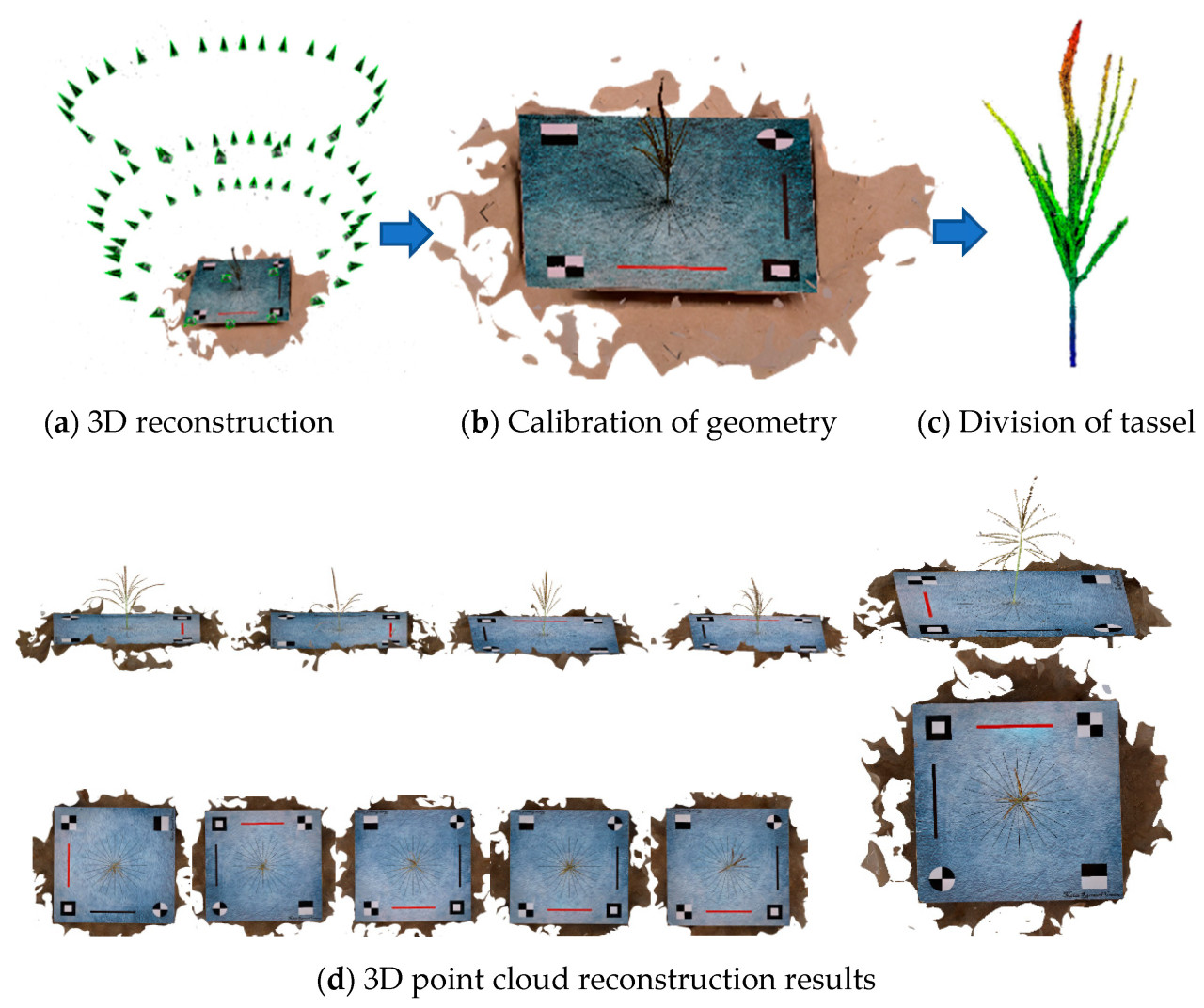
В данном исследовании мы использовали отечественное коммерческое программное обеспечение DJI Terra (Shenzhen DJI Technology Co., Ltd., Шэньчжэнь, Китай, версия 3.6.8) для пакетной реконструкции трёхмерных данных облака точек в формате .ply. Эти данные включают не только координаты X, Y и Z, но и цветовую информацию RGB. На рисунке 3 показан процесс реконструкции облака точек и некоторые результаты реконструкции, при этом все 1227 образцов были успешно реконструированы.

После создания облака точек пространственная информация трёхмерной реконструкции не согласуется с физическими значениями, и для точной количественной оценки параметров фенотипа спайка требуется дополнительная калибровка. Как показано на рисунке 3b , калибровка была достигнута путём построения красных и чёрных калибровочных линий на калибровочной доске стандартной длины 25 см, а координаты облака точек могли быть откалиброваны в абсолютной системе координат с помощью коэффициента вариации между прогнозируемыми и фактическими значениями, измеренного путём построения отношения между фактической длиной калибровочной линии (25 см) и значениями, полученными TreeQSM.

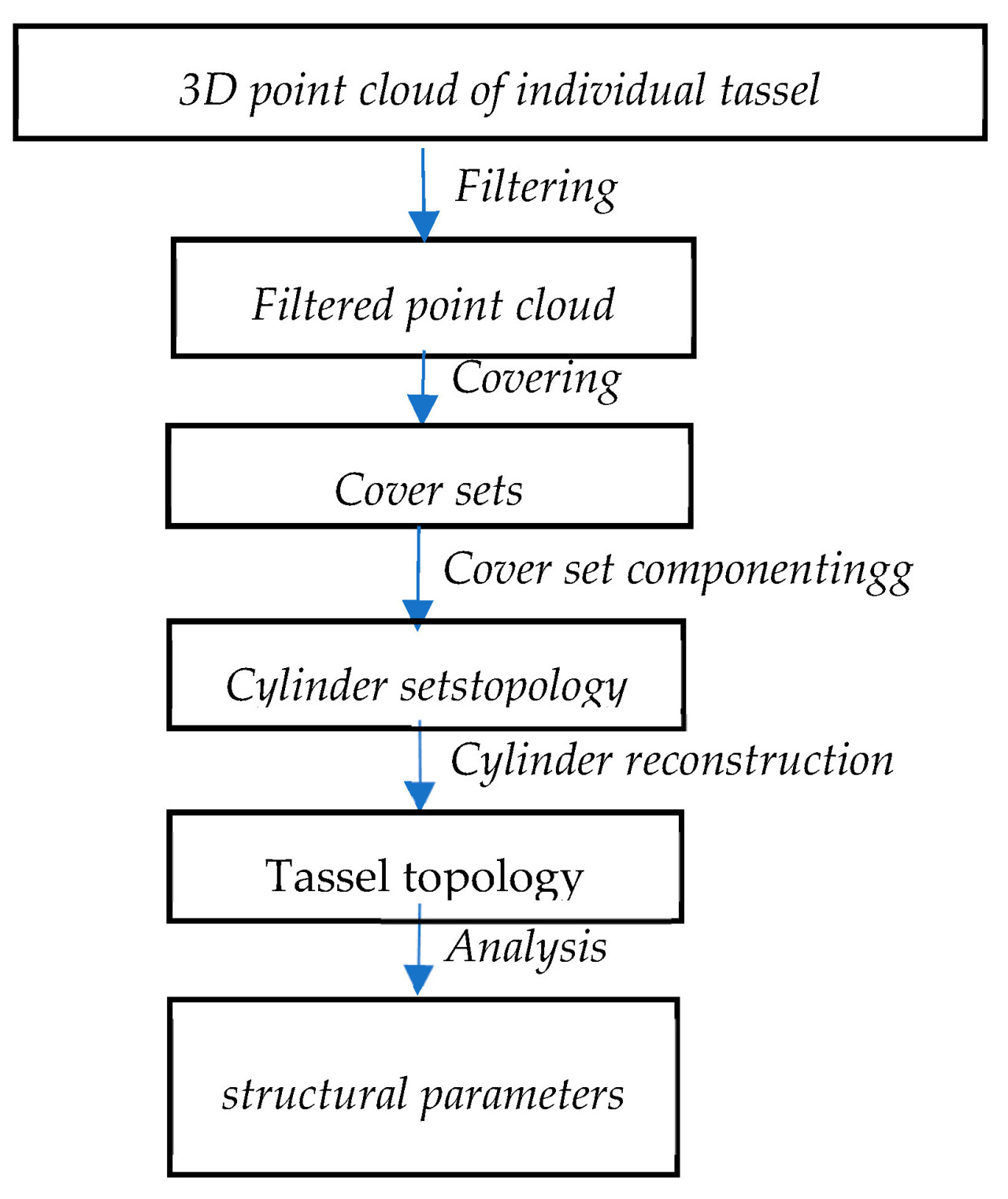
Как показано на рисунке 4 , сначала отфильтровываются шум и изолированные точки в облаке точек. Затем отфильтрованное облако точек сегментируется на небольшие множества, соответствующие поверхности кисточки, и определяются смежные отношения этих множеств покрытия. Затем множества, не принадлежащие кисточке, удаляются для определения компонентов кисточки. Компоненты кисточки относятся к практически независимым частям или кластерам в облаке точек, например, к отдельной ветви, группе ветвей или даже ко всей кисточке.

После этого при сегментации компонентов метелки используется модель поверхностного роста. Проверяя локальную связность, идентифицируются ветви. После этого каждая часть аппроксимируется последовательностью цилиндрических тел, которые могут иметь различные радиусы, длины и направления.

Наконец, на основе построенной цилиндрической модели рассчитывается топология кисточки и другие ее параметры.

Поскольку для извлечения параметров облака точек требуются данные, содержащие только интересующий объект, необходима дальнейшая фильтрация и кластеризация облака точек. Как показано на рисунке 5 , исходное облако точек подвергается гауссовой фильтрации и кластеризации с помощью DBSCAN для получения облака точек, содержащего только саму метку.

Процесс гауссовой фильтрации выполняется непосредственно в MATLAB 2017b с помощью функции pcdenoise (noisyData, «NumComponents», numComponents), где numComponents равен 0,1. После фильтрации используется функция кластеризации DBSCAN (eps = 0,5, min_samples = 150) для извлечения облака точек отдельных кисточек. Процесс показан на рисунке 5 .

Результаты предварительной обработки показывают, что из 1227 образцов метелок успешно выделено 1152, что соответствует уровню успешности 93,9%. Остальные образцы были отделены вручную.

2.4. Извлечение фенотипических параметров для метелки кукурузы

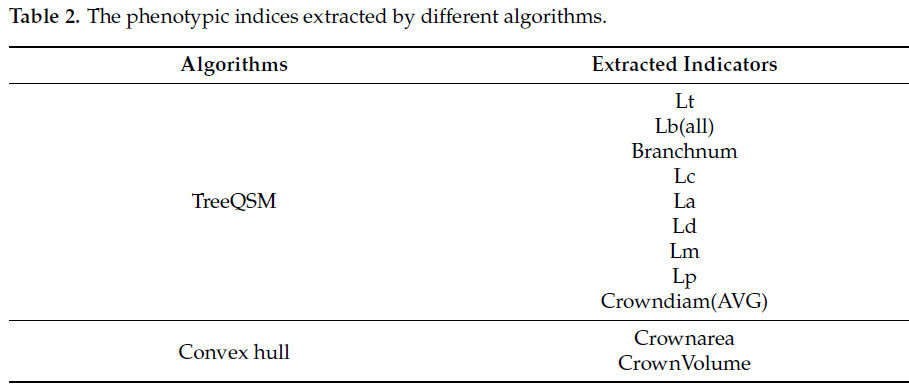
Для извлечения фенотипической информации используются алгоритмы TreeQSM и Convex Hull. Метрики, извлекаемые этими методами, приведены в таблице 2. Алгоритм TreeQSM широко применяется для извлечения трёхмерной структуры деревьев [ 45 , 46 ] и демонстрирует превосходные результаты. В настоящее время этот алгоритм доступен в различных версиях программного обеспечения [ 47 , 48 , 49 , 50 ].

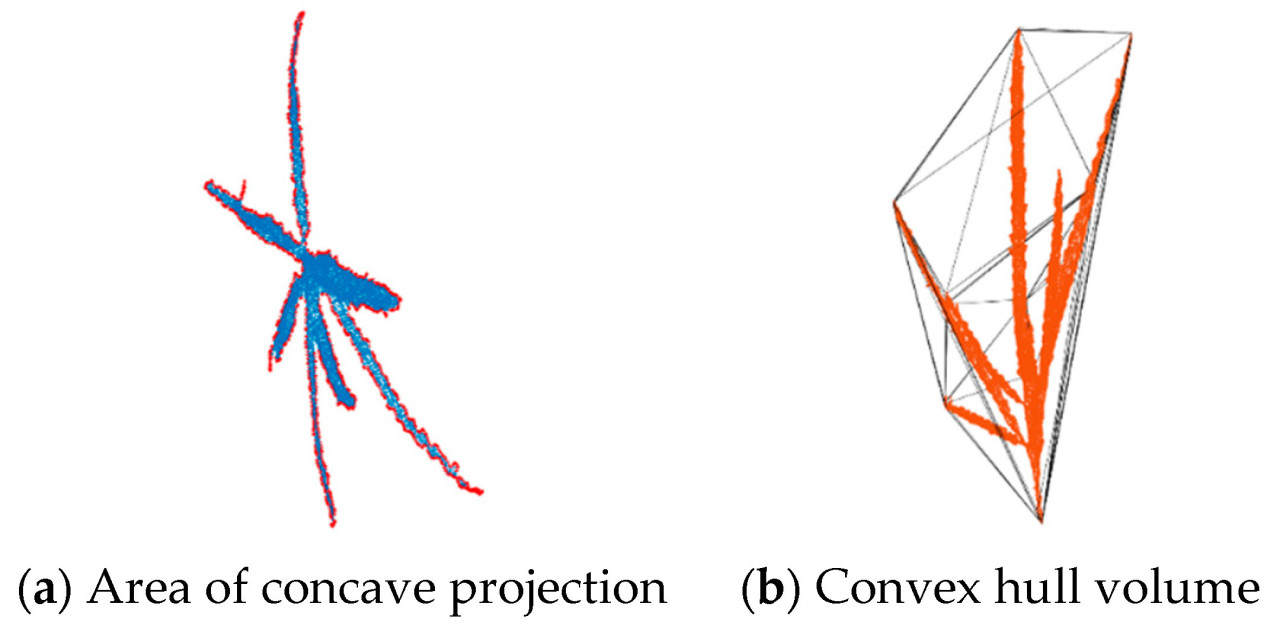
Предыдущие исследования показали, что пространственная изменчивость вдоль осей x, y и z точечных облаков топологии метелки кукурузы, реконструированных с использованием алгоритма TreeQSM и изображений, полученных с помощью этой системы, является стабильной, что демонстрирует высокую точность исходных точечных облаков. Кроме того, коэффициент корреляции между предсказанными и измеренными значениями нескольких фенотипических параметров имеет средний абсолютный коэффициент R2 > 0,9 [ 30 ]. При получении длины главного колоса необходимо удалить длину стебля. TreeQSM может записывать координаты самой низкой точки во время реконструкции топологической структуры (обычно координаты самой низкой точки стебля) и координаты первой ветви, а также категорию, длину и радиус всех сегментов подгонки цилиндра. Вычтите координаты самой низкой точки из координат первой ветви, чтобы получить длину стебля, а затем получите длину главного колоса. Для диаметра главного колоса и диаметра стебля это среднее значение всех подобранных диаметров цилиндров на главном колосе и стебле. В этом исследовании использовалась версия TreeQSM 2.4.1. TreeQSM имеет пять входных параметров: PatchDiam1, PatchDiam2Min, PatchDiam2Max, BallRad1 и BallRad2. В этом исследовании PatchDiam1, PatchDiam2Min и PatchDiam2Max были скорректированы для получения трехмерной топологической структуры метелок кукурузы и извлечения связанных фенотипических параметров [ 51 ]. Подробные правила корректировки параметров можно найти в справочных документах [ 52 ]. Результаты пространственного масштаба облака точек, извлеченные с помощью алгоритма TreeQSM, являются нефизическими величинами и требуют коррекции масштаба, чтобы гарантировать, что извлеченные результаты параметров фенотипа являются физическими величинами со стандартными единицами квантования. Как показано в Таблице 2 , метод выпуклой оболочки был использован для извлечения площади вогнутой короны ( Рисунок 6, а) и объёма выпуклой оболочки ( Рисунок 6, б) кисточки на плоскости проекции XOY. Площадь и объём короны были получены непосредственно с помощью граничной функции в MATLAB (версия 2017b), при этом третий параметр, представляющий степень рыхлости, был установлен равным 1.

2.5 Методы кластерного анализа

Во введении упоминается, что объектами данного исследования являются образцы кукурузы трёх генетических типов (NSS, TST и SS). Классификация этих образцов кукурузы основана на вероятностях генотипов, полученных с помощью программы STRUCTURE для определения структуры популяции и распределения генотипов по субпопуляциям.

Если вероятность наличия любого генотипа (NSS, TST или SS) превышает 60%, материал относится к этой категории. Если ни одна из долей не превышает 60%, материал относится к категории «СМЕШАННЫЙ». Поскольку классификация основана на вероятностях, исследование использует GFC для кластеризации 1227 образцов метелок кукурузы на основе структурных фенотипических параметров, полученных с помощью модели TreeQSM, с целью выявления различий в фенотипах структуры метелок между различными генотипами кукурузы.

В этом исследовании модель GFC используется для проведения кластерного анализа параметров фенотипа метелки кукурузы. GFC — это вероятностная модель, которая широко применяется в различных областях, таких как распознавание образов, компьютерное зрение, машинное обучение, интеллектуальный анализ данных и биоинформатика [ 53 , 54 , 55 ]. GFC объединяет концепции GFC. GFC позволяет точкам данных принадлежать нескольким кластерам с различной степенью принадлежности, а не быть жестко назначенными одному кластеру. GFC использует гауссовы функции для определения функции принадлежности, что приводит к нечеткому членству. Конкретно для этого исследования процесс кластеризации и ключевые переменные приведены ниже и в Таблице 3 :

Поскольку классификация генотипов материалов метелок кукурузы в данном исследовании основана на вероятностях, алгоритм GFC хорошо подходит для обработки различных генотипов материалов метелок.

В данном исследовании для анализа важности извлеченных параметров фенотипа метелки кукурузы использовался алгоритм случайного леса, который сравнивал их с результатами классификации GFC и проверял корректность результатов. С помощью модели случайного леса была проведена ранжировка важности 11 извлеченных параметров фенотипа метелки. При фиксированном случайном числе 42 70% данных были случайным образом отобраны в качестве обучающей выборки, а 30% — в качестве проверочной.

2.6 Оценка точности

Для оценки точности и эффективности кластеризации модели мы используем точность, прецизионность, полноту и F1, которые рассчитываются следующим образом:

где Tp прогнозируется как 1 и фактически равен 1; F P прогнозируется как 1, но фактически равен 0; Fn прогнозируется как 0, но фактически равен 1; Tn прогнозируется как 0 и фактически равен 0.

3.1 Результаты реконструкции трехмерной топологической структуры кисточки

В данном исследовании алгоритм TreeQSM был оптимизирован путём настройки трёх параметров (PatchDiam1, PatchDiam2Min и PatchDiam2Max) для достижения наилучших результатов реконструкции. Изначально значения параметров были установлены на 0,005, 0,0005 и 0,005 соответственно, что привело к успешной трёхмерной топологической реконструкции для 986 образцов с вероятностью успеха 80,3%. После дальнейшей настройки параметров количество успешно реконструированных метёлок увеличилось до 1194, что дало итоговую вероятность успеха 97,3%. Неудачные реконструкции были обусловлены в основном чрезмерно компактной формой метёлки, что затрудняло правильное разделение главного колоса и ветвей. Такие данные были исключены из последующего статистического анализа.

На рисунке 7 представлены результаты реконструкции TreeQSM для некоторых топологических структур метелок. Результаты показывают, что модель TreeQSM менее эффективна для метелок с более высокой компактностью. В основном наблюдаются два случая: один, когда главный стебель идентифицируется, но не может быть чётко отделен от ветвей, и другой, когда главный стебель полностью не идентифицируется. Оба случая считаются неудовлетворительными результатами извлечения. Напротив, для метелок с меньшей компактностью модель TreeQSM эффективно идентифицирует главный колос и ветви, обеспечивая необходимые условия для дальнейшего извлечения параметров структурного фенотипа метелки.

3.2 Анализ изменчивости облака точек и результаты извлечения

Параметры, извлечённые с помощью модели TreeQSM, всё ещё находятся в пределах евклидова расстояния и требуют коррекции. Процесс коррекции и точность результатов были проверены [ 30 ]. Абсолютный коэффициент вариации P набора данных в данном исследовании составляет от 34 до 39, но более 84% выборок имеют коэффициент вариации от 36 до 38, что говорит об относительно небольшой пространственной изменчивости облаков точек, полученных в тех же условиях.

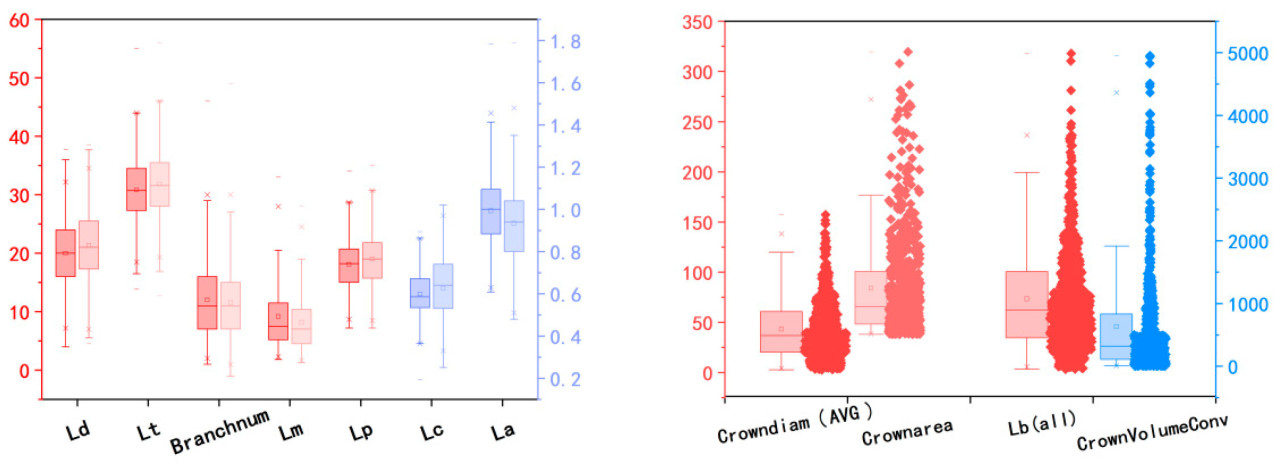
В этом исследовании анализировалось распределение данных по 11 извлеченным параметрам, как показано на рисунке 8. Все фенотипические параметры, за исключением количества ветвей, измеряются в сантиметрах. Левая сторона каждого набора сравнительных данных на рисунке 6 а представляет собой измеренное значение, а правая сторона - извлеченное модельное значение. Четыре левых набора данных соответствуют меткам шкалы слева, в то время как два правых набора данных соответствуют меткам шкалы справа. Из рисунка 6 очевидно, что медианное, среднее, минимальное и максимальное значения длины стебля и длины главного колоса больше измеренных. Это в первую очередь потому, что модель TreeQSM обеспечивает более подробные расчеты длины, тогда как измеренные данные, хотя и выпрямлены, не могут быть полностью выпрямлены, чтобы избежать поломки метелки. Кроме того, максимальный диаметр кроны, высота кроны, диаметр стебля и диаметр главного колоса показывают значительные расхождения между измеренными и извлеченными значениями. Это в основном из-за сложности точного измерения максимального диаметра кроны и высоты кроны и меньших значений диаметров ствола и главного колоса, которые подвержены большим ошибкам измерения. Средний диаметр кроны, общая длина ветвей, площадь кроны и объем выпуклой оболочки - все это результаты, извлеченные с помощью TreeQSM. Примечательно, что средний диаметр кроны отображается как десятикратное увеличение его извлеченного значения. Левый вертикальный стержень представляет собой красную шкалу данных ящика с единицами в см для среднего диаметра кроны и общей длины ветвей и см2 для площади кроны. Правый вертикальный стержень, синего цвета, представляет объем выпуклой оболочки с единицами в см3 . Как показано на рисунке 6 , средние значения для этих четырех фенотипических параметров значительно выше медианных значений, что указывает на то, что более 50% значений выборки распределены ниже среднего.

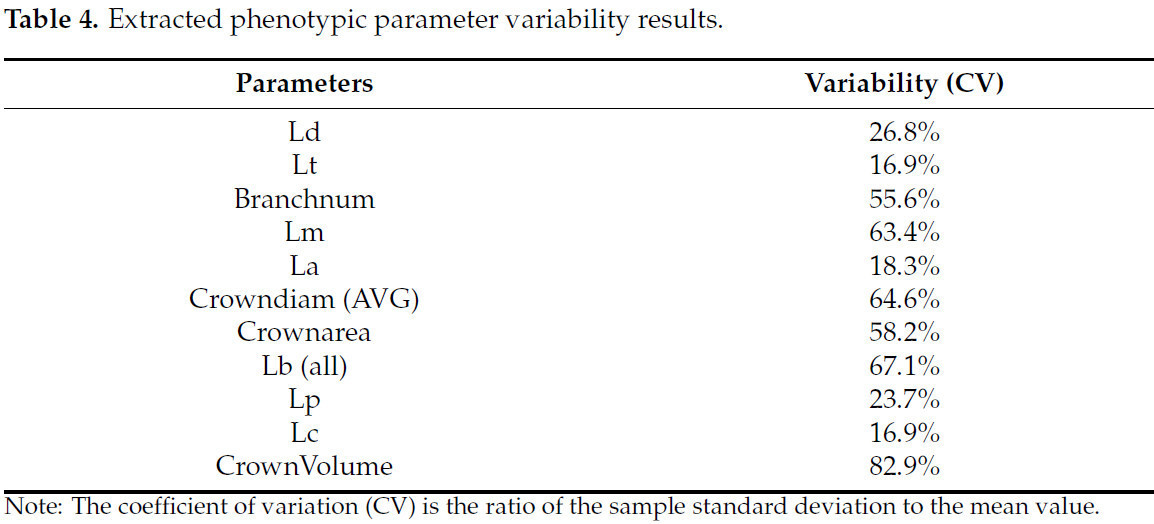
Кроме того, в данном исследовании была проанализирована изменчивость 11 извлеченных параметров, как показано в Таблице 4. Результаты показывают, что извлеченные фенотипические параметры демонстрируют значительную изменчивость, что отражает неконцентрированное распределение данных и обеспечивает более репрезентативную основу для результатов исследования.

3.3 Результаты анализа корреляций и значимости фенотипических параметров

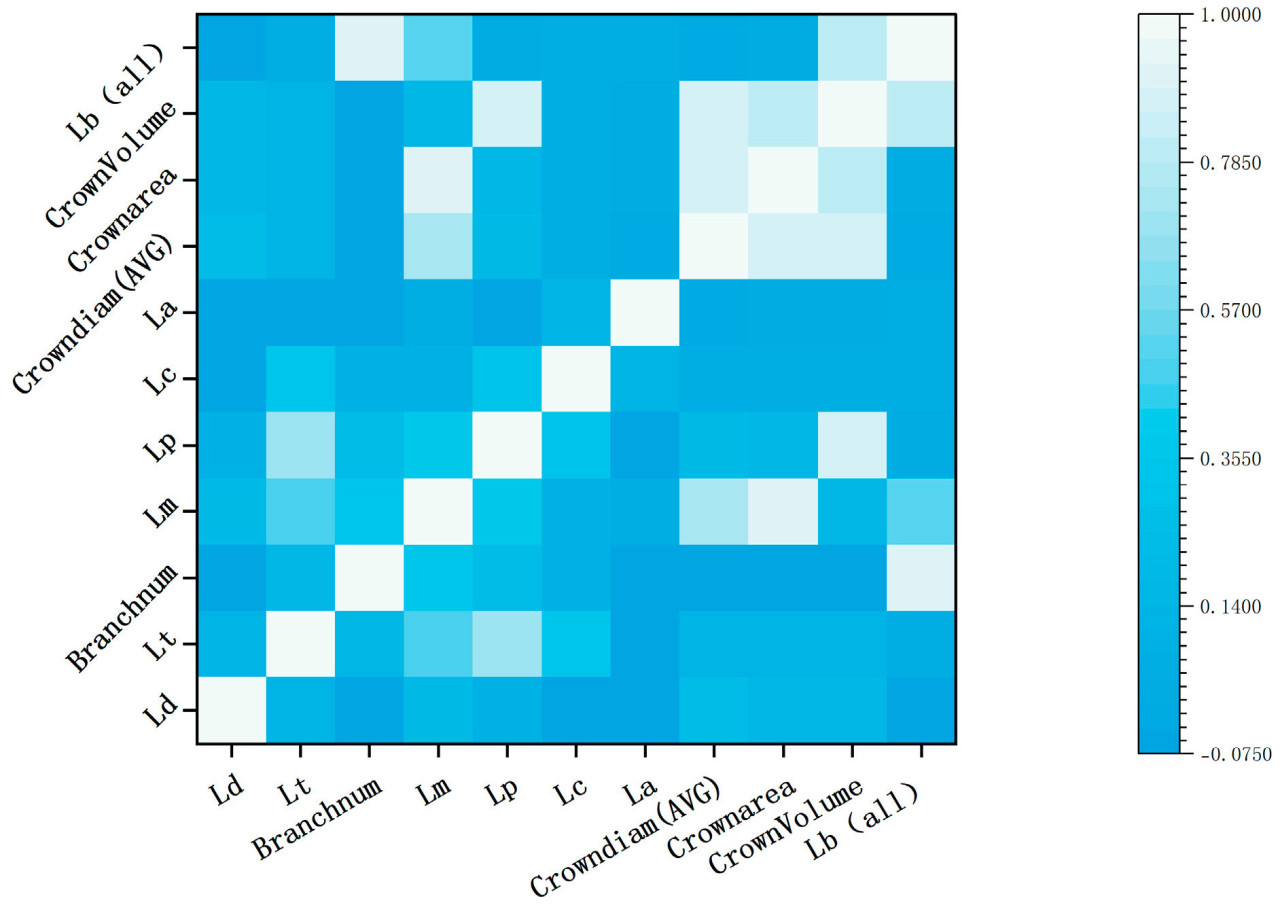
Используя метод коэффициента корреляции Пирсона, были построены корреляции между 11 фенотипическими параметрами метелок кукурузы, извлеченными с помощью TreeQSM. Как показано на рисунке 9 , наиболее высокая корреляция была обнаружена между количеством ветвей метелки и общей длиной ветвей, а также между площадью коронки и объёмом выпуклой оболочки, оба показателя превышали 0,9. Средний диаметр коронки показал следующую по величине корреляцию с площадью коронки и объёмом выпуклой оболочки, оба показателя превышали 0,8. Напротив, корреляции между диаметром главного колоса, диаметром стебля и длиной стебля были относительно ниже.

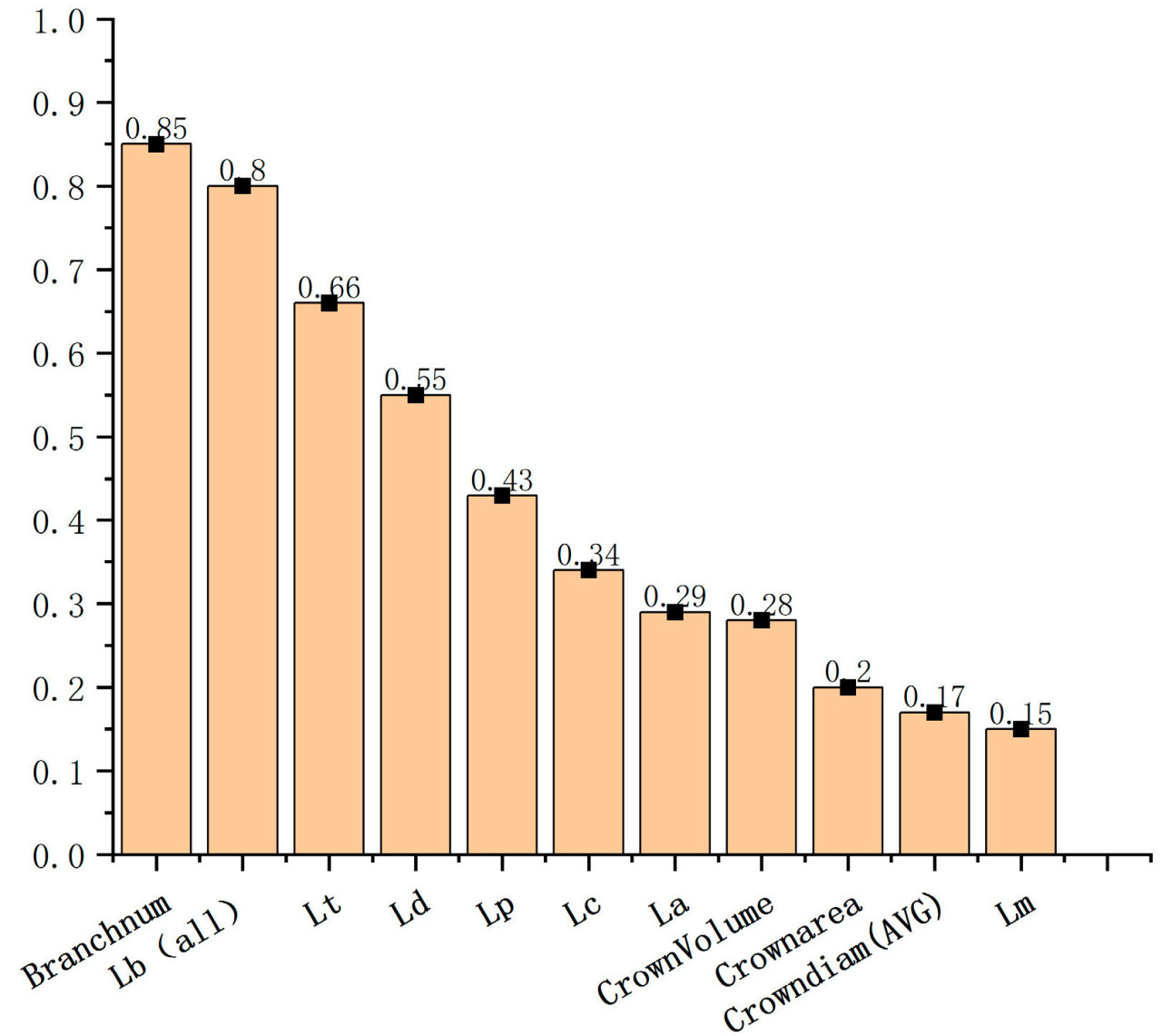
Значимость 11 параметров фенотипа кукурузы, рассчитанных с помощью алгоритма Random Forest, показана на рисунке 10. Можно заметить, что для классификации генотипов кукурузы тремя наиболее важными фенотипическими параметрами являются количество ветвей (Branchnum), общая длина ветвей (Lb (all)) и длина главного колоса (Lt). Наименее важными параметрами являются объём выпуклой оболочки кроны (CrownVolume), средний диаметр кроны (Crowndiam (AVG)) и площадь проекции кроны (Crownarea).

3.4. Результаты классификации различных генотипов

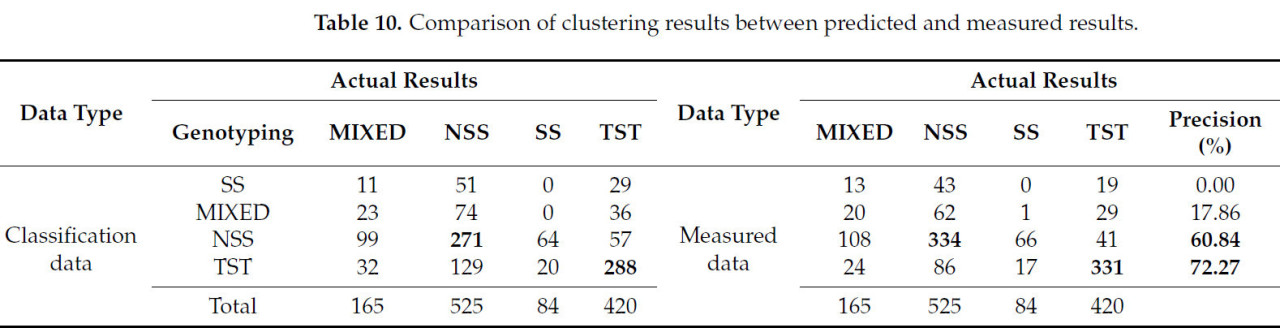
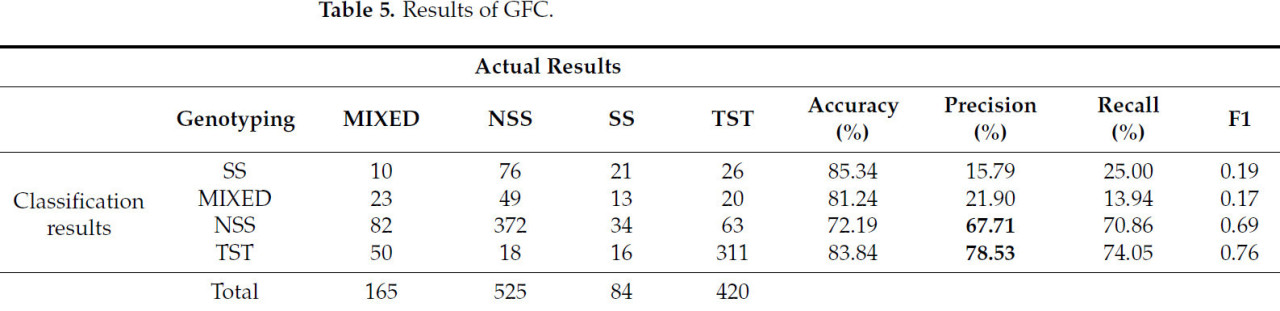
В этом исследовании была выполнена вероятностная кластеризация с использованием GFC для 10 из 11 извлеченных фенотипических параметров метелок кукурузы (исключая объем выпуклой оболочки). Количество кластеров было установлено равным 4, а количество итераций – 2000, что позволило рассчитать вероятность принадлежности каждого образца к каждому кластеру. Каждому образцу была присвоена вероятность принадлежности к определенному кластеру с вероятностями ≥ 0,6, используемыми для классификации образцов по категориям NSS, SS, TST или MIXED. Результаты представлены в Таблице 4. Столбцы представляют четыре результата кластеризации GFC, а строки указывают количество образцов для каждого генотипа в фактических результатах кластеризации.

Как показано в Таблице 5 , числа в таблице представляют собой фактическое количество образцов генотипов в каждой категории результатов классификации, а порядок объема данных четырех кластеров классификации также согласуется с объемом выборки, который представляет собой NSS, TST, MIXED и SS в порядке убывания. В третьем и четвертом кластерах точность классификации NSS и TST составляет 67,7% и 78,5% соответственно, а точность кластеризации NSS ниже, чем у TST. Одной из важных причин этого является то, что изменчивость фенотипических признаков больше в материале генотипа NSS, чем в TST. Кроме того, в результатах классификации есть категория MIXED, вероятности NSS и TST близки друг к другу, и ни одна из них не превышает 0,6, что вносит определенную степень случайности в распределение NSS и TST. Это также напрямую влияет на способность текущих методов классификации дополнительно повышать точность классификации NSS и TST.

3.5 Сравнение результатов кластеризации по различным фенотипическим параметрам

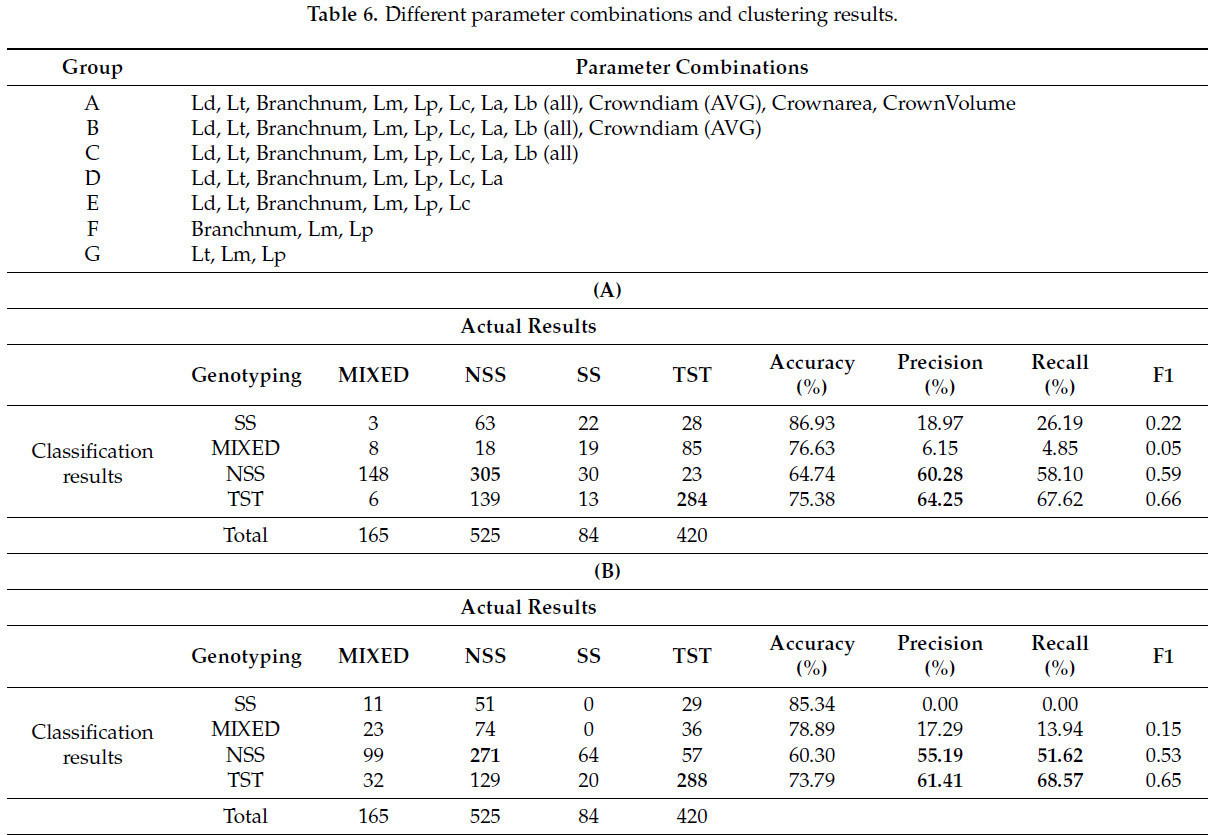
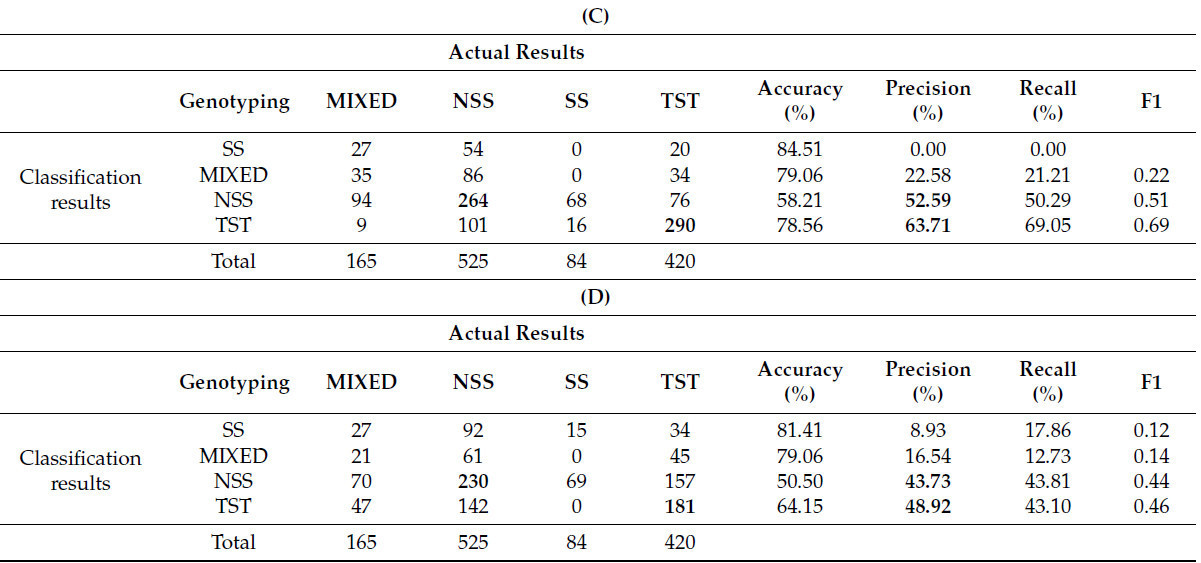
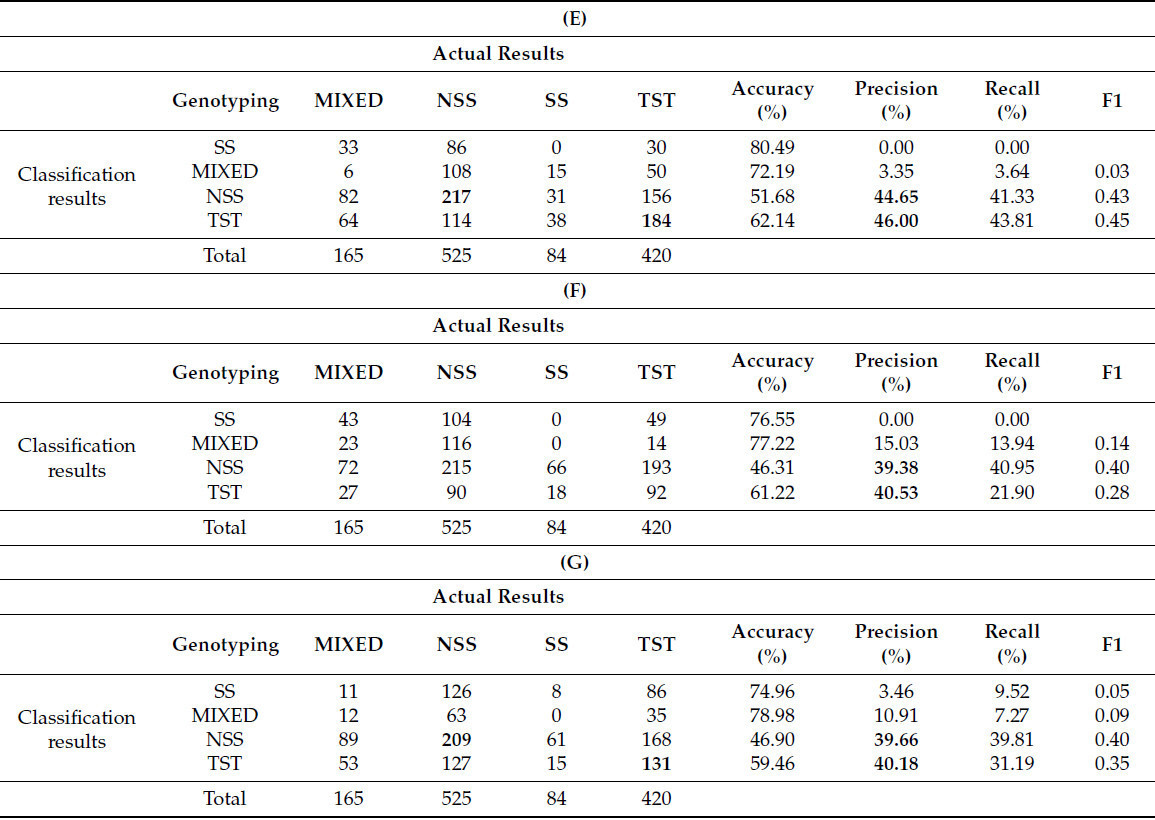
В данном исследовании 11 извлеченных фенотипических параметров были случайным образом объединены и затем кластеризованы. Комбинации параметров представлены в таблице 6 , где всего семь различных комбинаций обозначены буквами от A до G. Каждая последующая комбинация содержит на один параметр меньше предыдущей. Для вероятностной кластеризации снова использовался GFC, при этом выборки были разделены на четыре кластера и классифицированы на основе вероятностей ≥ 0,6. Примечательно, что комбинации F и G, имевшие меньше параметров, были исключены, поскольку GFC больше не мог выполнять точную кластеризацию с этими комбинациями.

Результаты кластеризации различных параметров ( таблица 6 ) показывают, что точность для категорий SS и MIXED остаётся относительно низкой. Точность кластеризации для генотипов NSS и TST постепенно снижается с уменьшением количества параметров. В частности, наблюдается значительное снижение точности при переходе от комбинаций C к D, что указывает на значительный вклад длины ветви в классификацию генотипа и на большую её изменчивость. С уменьшением количества параметров кластеризации точность продолжает снижаться.

4.1 Сравнение результатов различных методов кластеризации

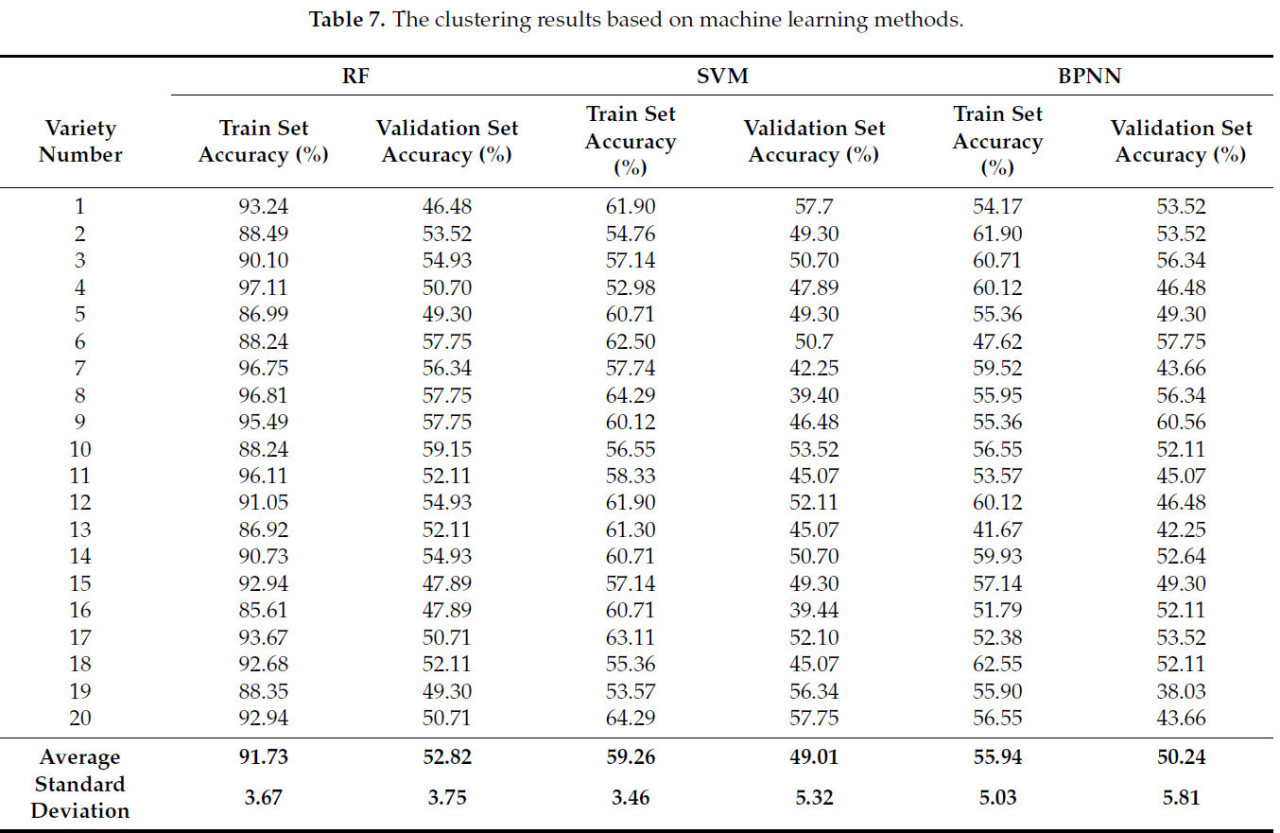
Результаты, полученные с помощью различных методов кластеризации, различаются. В этом исследовании сравнивались эффекты кластеризации трех распространенных методов машинного обучения, а именно: машины опорных векторов (SVM), случайного леса и нейронной сети обратного распространения (BP), а также трех распространенных алгоритмов, а именно: k-средних, иерархической кластеризации (HCM) и нечеткой кластеризации C-средних (FCM). Как было установлено в предыдущем исследовании, использование 10 фенотипических параметров для кластеризации по четырем категориям может обеспечить наивысшую точность. Поэтому в этом исследовании для сравнения результатов использовались те же 10 фенотипических параметров. Данные выборки были случайным образом разделены на 20 групп обучающих и проверочных наборов в соотношении 7:3. Точность кластеризации рассчитывалась на основе доли правильно классифицированных образцов от общего числа. Результаты кластеризации показаны в Таблице 7. При сравнении этих трех алгоритмов машинного обучения случайный лес демонстрирует наивысшую точность как на обучающем, так и на проверочном наборе, но его преимущество невелико. Точность метода составляет от 50% до 60%, а относительно более высокая точность на обучающей выборке также обусловлена ​​явлением переобучения. Судя по результатам, точность всех трёх методов невысока, и различия между ними также незначительны. Это связано с тем, что все три метода являются методами контролируемой классификации и не подходят для решения нелинейной задачи кластеризации фенотипов и генотипов кукурузы.

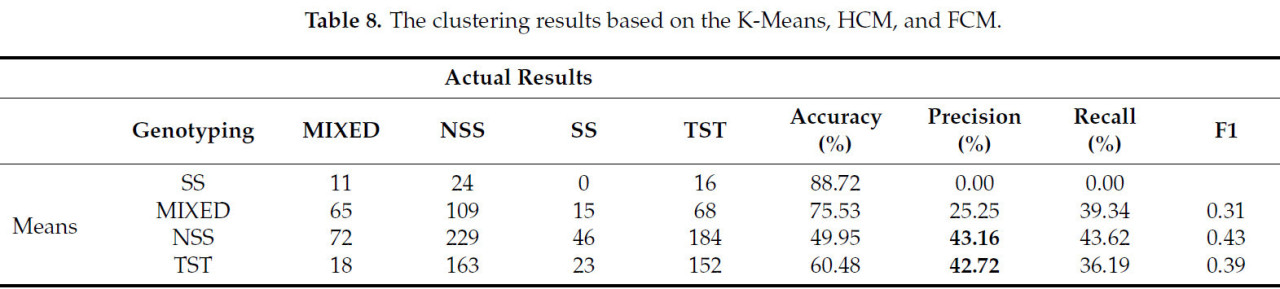
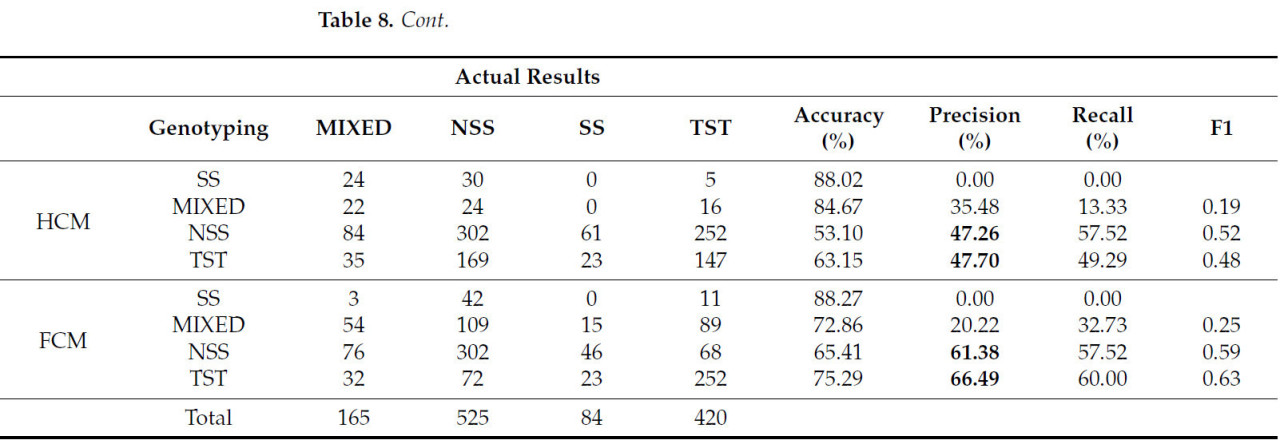
Сравнивая результаты кластеризации, полученные тремя другими методами, представленными в таблице 8 , можно обнаружить, что их точность кластеризации на 6–13% ниже, чем у GFC. Возможная причина заключается в том, что GFC обладает такими характеристиками, как нечёткость, вероятностный характер и чувствительность к нормально распределённым данным, в то время как правила классификации генотипов кукурузного материала, использованные в данном исследовании, также основаны на вероятности, а данные выборки также демонстрируют характеристики приблизительно нормального распределения.

4.2 Результаты кластеризации при различных режимах кластеризации

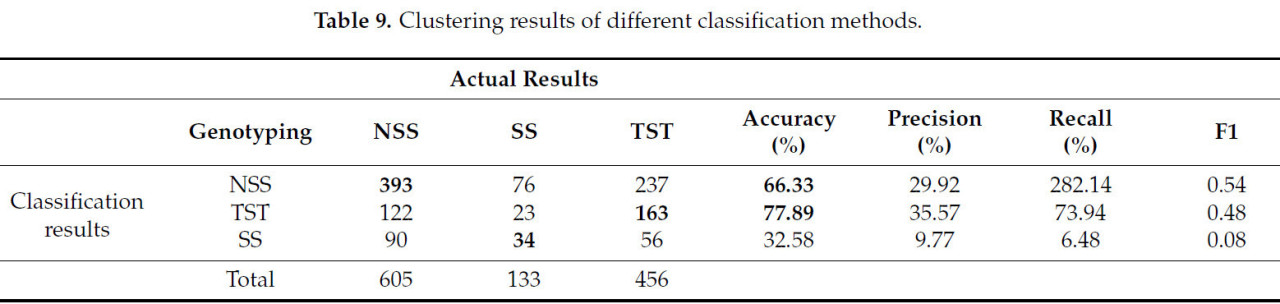
В разделе предыдущих результатов это исследование кластеризовало данные по четырем типам. Однако тип «смешанный» не принадлежит к определенному генетическому типу материалов кукурузы. Это исследование изучает удаление категории «смешанный». Исходные образцы MIXED были перераспределены по SS, NSS или TST на основе наибольшей вероятности доли. Результаты показаны в Таблице 9. Номера перераспределенных образцов были NSS: 605, SS: 133 и TST: 456. Затем новые образцы были подвергнуты GFC с использованием 10 параметров. Точность классификации NSS составила 55,7% в первом результате кластеризации, точность генотипа TST составила 52,9% во втором результате кластеризации, а точность SS составила 18,9% в третьем результате кластеризации. По сравнению с классификацией по четырем категориям точность значительно снизилась.

4.3 Сравнение с результатами кластеризации измеренных значений

В этом исследовании восемь реально измеренных количественных фенотипических признаков, отличных от площади коронки метелки кукурузы, объема выпуклой головни и среднего диаметра коронки (данные, которые невозможно было измерить реалистично), были проанализированы в соответствии с кластеризацией; выборки данных были такими же, как 1194 группы, используемые алгоритмом GFC, и результаты показаны в Таблице 10. Здесь можно увидеть, что точность кластеризации реально измеренных данных была улучшена по сравнению с точностью автоматизированной кластеризации этой платформы фенотипирования, из которых точность кластеризации генотипов NSS была улучшена, NSS на 5,64% и TST на 10,86% (точность классификации системы в этом исследовании составила 51,62% и 68,57%), что указывает на то, что эффект кластеризации генотипов метелки кукурузы с использованием методологии этого исследования заслуживает доверия и имеет некоторое контрольное значение.

В данном исследовании система TIPS использовалась для автоматического получения изображений мужских метелок кукурузы, а алгоритм SFM – для синтеза последовательности изображений в трёхмерное облако точек. Алгоритм гауссовского фильтра и алгоритм DBSCAN использовались для подавления шума в исходном облаке точек, а также для разделения и извлечения облака точек мужской метелки одного растения. На основе извлеченного облака точек система TIPS использовалась для реализации системы, предназначенной специально для извлечения древовидной структуры с использованием алгоритма TreeQSM для реконструкции трёхмерного облака точек метелки кукурузы. В данном исследовании были изучены реконструкция топологии мужского початка, извлечение множественных структурно-фенотипических параметров и, наконец, анализ извлечённых структурно-фенотипических параметров с использованием генотипов материалов кукурузы с помощью алгоритма кластеризации GFC, который реализует технический анализ всего набора процессов от извлечения фенотипических параметров до классификации генотипов. Основные достижения включают следующее:

(а)  Разработанная в данном исследовании система обладает высокой эффективностью и точностью для извлечения структурных фенотипов метелки кукурузы с высокой точностью, особенно использование комбинации гауссовой фильтрации и алгоритмов DBSCAN для достижения разделения облака точек метелки одного растения оказалось очень эффективным.

(б)  Для классификации генотипов материалов кукурузы важным параметром был Branchnum > Lb (all) > Lt > Ld > Lp > Lc > La > Lm > Crownarea > Crowndiam (AVG) > CrownVolume, который выявил величину изменчивости фенотипических параметров метелки различных генотипов материалов кукурузы.

(с)  По сравнению с традиционными методами RF, SVM и BPNN, основанными на контролируемой классификации, алгоритм GFC, метод неконтролируемой классификации, более эффективно разделил генотипы кукурузы NSS и TST с точностью 67,7% и 78,5%.

(г)  Сравнивая результаты кластеризации измеренных данных и прогнозируемых данных, можно отметить, что, хотя точность кластеризации измеренных данных на 5–10% выше, чем у прогнозируемых данных, метод в данном исследовании имеет более высокую экономическую и практическую ценность.

(е)  По сравнению с традиционным процессом классификации материалов кукурузы с использованием информации о локусах генов, который является сложным, трудоёмким и дорогостоящим, данное исследование стало первым исследованием кластеризации генотипов кукурузы с использованием фенотипических параметров метёлок кукурузы и доказало, что его результаты более эффективны, экономичны, просты в использовании и высокоточны. Размытость, вероятностный характер и чувствительность к данным нормального распределения алгоритма гауссовой нечёткой кластеризации соответствуют правилам классификации генотипов материалов кукурузы и характеристикам выборочных данных, использованных в данном исследовании. Следовательно, он обладает относительно хорошей точностью классификации.

(ж)  Фенотип – результат действия генов. Изменчивость числа ветвей, длины ветвей и длины главного колоса, а также точность кластеризации, полученные в данном исследовании, убедительно демонстрируют относительно высокую наследуемость фенотипических признаков метелки у различных генотипов кукурузы.

В данном исследовании мы изучили изменчивость признаков различных генотипов с точки зрения трехмерной структуры и фенотипа метелки кукурузы, что является важным инструментом для эффективного скрининга материалов кукурузы.

1.    Gebbers, R.; Adamchuk, V.I. Precision agriculture and food security. Science 2010, 327, 828–831. [Google Scholar] [CrossRef] [PubMed]

2.    Tester, M.; Langridge, P. Breeding technologies to increase crop production in a changing world. Science 2010, 327, 818–822. [Google Scholar] [CrossRef] [PubMed]

3.    Shakoor, N.; Lee, S.; Mockler, T.C. High throughput phenotyping to accelerate crop breeding and monitoring of diseases in the field. Curr. Opin. Plant Biol. 2017, 38, 184–192. [Google Scholar] [CrossRef]

4.    Han, D.; Yang, G.; Yang, H.; Qiu, C.; Chen, M.; Wen, W.; Niu, Q.; Yang, W. Three Dimensional Information Extraction from Maize Tassel Based on Stereoscopic Vision; Chinese Society of Agricultural Engineering: Beijing, China, 2018. [Google Scholar]

5.    Geraldi, I.; Miranda Filho, J.; Vencovsky, R. Estimates of genetic parameters for tassel characters in maize (Zea mays L.) and breeding perspectives. Maydica 1985, 30, 1–14. [Google Scholar]

6.    Liu, J.; Bai, Z.; Wu, W. Evolution of main ear traits of maize hybrids and their effects on breeding objectives. Maize Sci. 2004, 12 (Suppl. S2), 3–4. [Google Scholar]

7.    Xu, G.; Wang, X.; Huang, C.; Xu, D.; Li, D.; Tian, J.; Chen, Q.; Wang, C.; Liang, Y.; Wu, Y. Complex genetic architecture underlies maize tassel domestication. New Phytol. 2017, 214, 852–864. [Google Scholar] [CrossRef]

8.    Berke, T.; Rocheford, T. Quantitative trait loci for tassel traits in maize. Crop Sci. 1999, 39, 1439–1443. [Google Scholar] [CrossRef]

9.    Upadyayula, N.; Da Silva, H.; Bohn, M.O.; Rocheford, T. Genetic and QTL analysis of maize tassel and ear inflorescence architecture. Theor. Appl. Genet. 2006, 112, 592–606. [Google Scholar] [CrossRef] [PubMed]

10. Zhou, Y.; Kusmec, A.; Mirnezami, S.V.; Attigala, L.; Srinivasan, S.; Jubery, T.Z.; Schnable, J.C.; Salas-Fernandez, M.G.; Ganapathysubramanian, B.; Schnable, P.S. Identification and utilization of genetic determinants of trait measurement errors in image-based, high-throughput phenotyping. Plant Cell 2021, 33, 2562–2582. [Google Scholar] [CrossRef] [PubMed]

11. Wang, X.; Li, J.; Han, L.; Liang, C.; Li, J.; Shang, X.; Miao, X.; Luo, Z.; Zhu, W.; Li, Z. QTG-Miner aids rapid dissection of the genetic base of tassel branch number in maize. Nat. Commun. 2023, 14, 5232. [Google Scholar] [CrossRef] [PubMed]

12. Xhu, B.; Liu, F.; Che, Y.; Hui, F.; Ma, Y. Three-dimensional quantification of intercropping crops in field by ground and aerial photography. In Proceedings of the 2018 6th International Symposium on Plant Growth Modeling, Simulation, Visualization and Applications (PMA), Hefei, China, 4–8 November 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 8–12. [Google Scholar] [CrossRef]

13. Zhang, X.; Huang, C.; Wu, D.; Qiao, F.; Li, W.; Duan, L.; Wang, K.; Xiao, Y.; Chen, G.; Liu, Q. High-throughput phenotyping and QTL mapping reveals the genetic architecture of maize plant growth. Plant Physiol. 2017, 173, 1554–1564. [Google Scholar] [CrossRef]

14. Das Choudhury, S.; Samal, A.; Awada, T. Leveraging image analysis for high-throughput plant phenotyping. Front. Plant Sci. 2019, 10, 508. [Google Scholar] [CrossRef] [PubMed]

15. Das Choudhury, S.; Maturu, S.; Samal, A.; Stoerger, V.; Awada, T. Leveraging image analysis to compute 3D plant phenotypes based on voxel-grid plant reconstruction. Front. Plant Sci. 2020, 11, 521431. [Google Scholar] [CrossRef] [PubMed]

16. Hartmann, A.; Czauderna, T.; Hoffmann, R.; Stein, N.; Schreiber, F. HTPheno: An image analysis pipeline for high-throughput plant phenotyping. BMC Bioinform. 2011, 12, 148. [Google Scholar] [CrossRef]

17. Gage, J.L.; Miller, N.D.; Spalding, E.P.; Kaeppler, S.M.; de Leon, N. TIPS: A system for automated image-based phenotyping of maize tassels. Plant Methods 2017, 13, 21. [Google Scholar] [CrossRef] [PubMed]

18. Klukas, C.; Chen, D.; Pape, J.-M. Integrated analysis platform: An open-source information system for high-throughput plant phenotyping. Plant Physiol. 2014, 165, 506–518. [Google Scholar] [CrossRef] [PubMed]

19. Gibbs, J.A.; Pound, M.; French, A.P.; Wells, D.M.; Murchie, E.; Pridmore, T. Approaches to three-dimensional reconstruction of plant shoot topology and geometry. Funct. Plant Biol. 2016, 44, 62–75. [Google Scholar] [CrossRef] [PubMed]

20. Li, J.; Tang, L. Developing a low-cost 3d plant morphological traits characterization system. Comput. Electron. Agric. 2017, 143, 1–13. [Google Scholar] [CrossRef]

21. Yang, W.; Guo, Z.; Huang, C.; Duan, L.; Chen, G.; Jiang, N.; Fang, W.; Feng, H.; Xie, W.; Lian, X. Combining high-throughput phenotyping and genome-wide association studies to reveal natural genetic variation in rice. Nat. Commun. 2014, 5, 5087. [Google Scholar] [CrossRef]

22. Guo, W.; Fukatsu, T.; Ninomiya, S. Automated characterization of flowering dynamics in rice using field-acquired time-series rgb images. Plant Methods 2015, 11, 7. [Google Scholar] [CrossRef]

23. Lu, H.; Cao, Z.; Xiao, Y.; Fang, Z.; Zhu, Y.; Xian, K. Fine-grained maize tassel trait characterization with multi-view representations. Comput. Electron. Agric. 2015, 118, 143–158. [Google Scholar] [CrossRef]

24. Kükenbrink, D.; Schneider, F.D.; Leiterer, R.; Schaepman, M.E.; Morsdorf, F. Quantification of hidden canopy volume of airborne laser scanning data using a voxel traversal algorithm. Remote Sens. Environ. 2017, 194, 424–436. [Google Scholar] [CrossRef]

25. Kunz, M.; Hess, C.; Raumonen, P.; Bienert, A.; Hackenberg, J.; Maas, H.; Härdtle, W.; Fichtner, A.; Von Oheimb, G. Comparison of wood volume estimates of young trees from terrestrial laser scan data. iFor. Biogeosci. For. 2017, 10, 451–458. [Google Scholar] [CrossRef]

26. Thapa, S.; Zhu, F.; Walia, H.; Yu, H.; Ge, Y. A novel LiDAR-based instrument for high-throughput, 3D measurement of morphological traits in maize and sorghum. Sensors 2018, 18, 1187. [Google Scholar] [CrossRef]

27. Paulus, S.; Behmann, J.; Mahlein, A.-K.; Plümer, L.; Kuhlmann, H. Low-cost 3d systems: Suitable tools for plant phenotyping. Sensors 2014, 14, 3001–3018. [Google Scholar] [CrossRef] [PubMed]

28. Chaivivatrakul, S.; Tang, L.; Dailey, M.N.; Nakarmi, A.D. Automatic morphological trait characterization for corn plants via 3d holographic reconstruction. Comput. Electron. Agric. 2014, 109, 109–123. [Google Scholar] [CrossRef]

29. Wu, S.; Wen, W.; Gou, W.; Lu, X.; Zhang, W.; Zheng, C.; Xiang, Z.; Chen, L.; Guo, X. A miniaturized phenotyping platform for individual plants using multi-view stereo 3D reconstruction. Front. Plant Sci. 2022, 13, 897746. [Google Scholar] [CrossRef]

30. Xu, B.; Wan, X.; Yang, H.; Feng, H.; Fu, Y.; Cen, H.; Wang, B.; Zhang, Z.; Li, S.; Zhao, C. TIPS: A three-dimensional phenotypic measurement system for individual maize tassel based on TreeQSM. Comput. Electron. Agric. 2023, 212, 108150. [Google Scholar] [CrossRef]

31. Song, D. Clustering Study of Gene Expression Data Based on Gaussian Mixture Model. Ph.D. Thesis, Jiangsu University, Zhenjiang, China, 2015. [Google Scholar]

32. Minton, R.L. Morphometrics Suggest Reduced Diversity in the Freshwater Snail Genus Gyrotoma Shuttleworth, 1845 (Gastropoda: Pleuroceridae). Ann. Carnegie Mus. 2021, 87, 79–88. [Google Scholar] [CrossRef]

33. Yang, M.-S.; Chang-Chien, S.-J.; Nataliani, Y. Unsupervised fuzzy model-based Gaussian clustering. Inf. Sci. 2019, 481, 1–23. [Google Scholar] [CrossRef]

34. Fuchs, R.; Pommeret, D.; Viroli, C. Mixed Deep Gaussian Mixture Model: A clustering model for mixed datasets. Adv. Data Anal. Classif. 2022, 16, 31–53. [Google Scholar] [CrossRef]

35. Yang, X.; Gao, S.; Xu, S.; Zhang, Z.; Prasanna, B.M.; Li, L.; Li, J.; Yan, J. Characterization of a global germplasm collection and its potential utilization for analysis of complex quantitative traits in maize. Mol. Breed. 2010, 28, 511–526. [Google Scholar] [CrossRef]

36. Pan, C.-X.; Hu, Y.; Ji, H.-B.; Li, Y.-M.; Chen, N.-L. Phenotypic diversity and clustering analysis of watermelon germplasm. J. Plant Genet. Resour. 2015, 16, 59–63. [Google Scholar]

37. Xie, Z.; Chen, S.; Gao, G.; Li, H.; Wu, X.; Meng, L.; Ma, Y. Evaluation of rapeseed flowering dynamics for different genotypes with UAV platform and machine learning algorithm. Precis. Agric. 2022, 23, 1688–1706. [Google Scholar] [CrossRef]

38. Han, L.; Yang, G.; Dai, H.; Yang, H.; Xu, B.; Feng, H.; Li, Z.; Yang, X. Fuzzy clustering of maize plant-height patterns using time series of UAV remote-sensing images and variety traits. Front. Plant Sci. 2019, 10, 926. [Google Scholar] [CrossRef]

39. Rincón Sánchez, F.; Johnson, B.; Crossa, J.; Taba, S. Cluster analysis, an approach to sampling variability in maize accessions. Agric. Food Sci. 1996, 41, 4. [Google Scholar]

40. Shrestha, J. Cluster analysis of maize inbred lines. J. Nepal Agric. Res. Counc. 2016, 2, 33–36. [Google Scholar] [CrossRef]

41. Pritchard, J.K.; Stephens, M.; Rosenberg, N.A.; Donnelly, P. Association mapping in structured populations. Am. J. Hum. Genet. 2000, 67, 170–181. [Google Scholar] [CrossRef]

42. Falush, D.; Stephens, M.; Pritchard, J.K. Inference of population structure using multilocus genotype data: Linked loci and correlated allele frequencies. Genetics 2003, 164, 1567–1587. [Google Scholar] [CrossRef] [PubMed]

43. Furukawa, Y.; Ponce, J. Accurate, dense, and robust multiview stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 1362–1376. [Google Scholar] [CrossRef]

44. Wu, C.; Zhan, S. Three-dimensional face modeling of SFM algorithm based on gabor feature. J. Hefei Univ. Technol. Nat. Sci. Ed. 2017, 40, 180–185. [Google Scholar] [CrossRef]

45. Dassot, M.; Colin, A.; Santenoise, P.; Fournier, M.; Constant, T. Terrestrial laser scanning for measuring the solid wood volume, including branches, of adult standing trees in the forest environment. Comput. Electron. Agric. 2012, 89, 86–93. [Google Scholar] [CrossRef]

46. Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]

47. Raumonen, P.; Casella, E.; Calders, K.; Murphy, S.; Åkerblom, M.; Kaasalainen, M. Massive-scale tree modelling from TLS data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 189–196. [Google Scholar] [CrossRef]

48. Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast automatic precision tree models from terrestrial laser scanner data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]

49. Hackenberg, J.; Spiecker, H.; Calders, K.; Disney, M.; Raumonen, P. SimpleTree—An efficient open source tool to build tree models from TLS clouds. Forests 2015, 6, 4245–4294. [Google Scholar] [CrossRef]

50. Delagrange, S.; Jauvin, C.; Rochon, P. PypeTree: A tool for reconstructing tree perennial tissues from point clouds. Sensors 2014, 14, 4271–4289. [Google Scholar] [CrossRef]

51. Moorthy, S.M.K.; Raumonen, P.; Van den Bulcke, J.; Calders, K.; Verbeeck, H. Terrestrial laser scanning for non-destructive estimates of liana stem biomass. For. Ecol. Manag. 2020, 456, 117751. [Google Scholar] [CrossRef]

52. Hackenberg, J.; Morhart, C.; Sheppard, J.; Spiecker, H.; Disney, M. Highly accurate tree models derived from terrestrial laser scan data: A method description. Forests 2014, 5, 1069–1105. [Google Scholar] [CrossRef]

53. Wei, X. EM Algorithm and Its Initialization for Parameter Estimation of Gaussian Mixture Models. Electron. Testing. 2011, 6, 26–30. [Google Scholar] [CrossRef]

54. Xing, C.; Zhao, Q.; Wang, X. Research on accelerated EM algorithm based on robust Gaussian mixture model. Comput. Appl. Res. 2017, 4, 1042–1046. [Google Scholar]

55. Wu, T. Application of Gaussian Mixture Model Based on EM Algorithm in Iris Dataset. Netw. Secur. Technol. Appl. 2022, 4, 47–49. [Google Scholar]

Xu B, Zhao C, Yang G, Zhang Y, Liu C, Feng H, Yang X, Yang H. Genotyping Identification of Maize Based on Three-Dimensional Structural Phenotyping and Gaussian Fuzzy Clustering. Agriculture. 2025; 15(1):85. https://doi.org/10.3390/agriculture15010085

Перевод статьи «Genotyping Identification of Maize Based on Three-Dimensional Structural Phenotyping and Gaussian Fuzzy Clustering» авторов Xu B, Zhao C, Yang G, Zhang Y, Liu C, Feng H, Yang X, Yang H., оригинал доступен по ссылке. Лицензия: CC BY. Изменения: переведено на русский язык