Преодоление «слепых зон»: улучшенная модель измерения объема кроны с учетом внутренних пустот
Точное измерение объема кроны в саду служит важной основой для регулирования скорости ветра и дозировки при точном управлении садоводством. Однако существующие методы измерения объема кроны не удовлетворяют требованиям высокой точности и работы в реальном времени, необходимым для точного дифференцированного применения средств в плодовых садах. Для решения этих задач в данном исследовании разработана модель измерения объема кроны для опрыскивания сада с использованием данных облака точек лидара.
Аннотация
В области извлечения признаков из облака точек предложен улучшенный алгоритм Alpha Shape для извлечения контуров облака точек. Этот метод усовершенствует проверку валидности сегментов контурных линий, эффективно снижая ошибки длины контура на каждой плоскости проекции 3D-облака точек. Дополнительно, улучшения в методе расчета объема с помощью интеграции сетки включают влияние просветов в кроне при вычислении разницы высот, что значительно повышает точность оценки объема кроны.
Для отбора признаков использован метод рекурсивного исключения признаков на основе случайного леса с перекрестной проверкой для фильтрации 10 признаков. В конечном итоге, для обучения модели были оставлены пять ключевых признаков: количество точек в облаке, 2D-контур облака точек вдоль направлений проекции X и Z, 2D-ширина в направлении проекции Y и 2D-длина в направлении проекции Z.
В процессе построения модели исследование оптимизировало гиперпараметры регрессии на основе метода частичных наименьших квадратов (PLSR), нейронных сетей с обратным распространением ошибки (BP) и градиентного бустинга деревьев решений (GBDT) для создания моделей измерения объема кроны, адаптированных к набору данных.
Результаты экспериментов показывают, что модель PLSR превзошла другие подходы, достигнув оптимальной производительности с тремя главными компонентами. Полученная модель измерения объема кроны достигла показателей R² = 0.9742, RMSE = 0.1879 и MAE = 0.1161. Эти результаты демонстрируют, что модель PLSR обладает сильной способностью к обобщению, минимальным смещением прогноза и низкой средней ошибкой прогноза, что предлагает ценную основу для точного контроля опрыскивания крон в садах.
1. Введение
Химическая борьба с вредителями и болезнями имеет важнейшее значение в управлении садом, при этом плодовые деревья требуют ежегодно от 8 до 15 обработок пестицидами [1], что составляет около 30% от общего объема работ по управлению садом [2]. Традиционные методы применения пестицидов, в основном основанные на опрыскивании по типу «высокая производительность, дождевание», страдают от низкой степени утилизации, составляющей всего от 20% до 40% [3]. Этот неэффективный метод приводит к значительным потерям пестицидов, чрезмерным остаткам в сельскохозяйственной продукции и загрязнению окружающей среды. Технология прецизионного дифференцированного применения пестицидов в садах использует датчики для идентификации целей и регулирует объем распыла и силу ветра на основе параметров, таких как местоположение цели, объем и плотность [4]. Этот подход эффективно преодолевает ограничения традиционных методов опрыскивания.
Точное применение распыла с использованием вентиляторных опрыскивателей требует как регулирования ветра, так и контроля дозировки [5]. Сила ветра и дозировка должны регулироваться на основе объема кроны и плотности ветвей внутри кроны для удовлетворения конкретных требований [6]. Соотношение объема пустот в кроне к общему объему кроны может в некоторой степени характеризовать плотность ветвей внутри кроны. Если измеренный объем зазоров в кроне мал, это может привести к недостаточной силе ветра и неадекватному применению пестицидов, что делает борьбу неэффективной. Напротив, если измеренный объем пустот в кроне велик, это может вызвать чрезмерную силу ветра и передозировку пестицидов, приводя к сносу распыла за пределы кроны плодового дерева, тем самым расходуя пестициды впустую и серьезно загрязняя сельскохозяйственную среду. Поэтому точное измерение объема кроны имеет большое значение для прецизионного применения пестицидов в садах.
Традиционный метод измерения объема кроны основан на ручных измерениях, в основном с использованием таких инструментов, как рулетки и высотомеры [7]. Этот подход измеряет ширину кроны, высоту и другие данные, рассчитывая объем кроны через установленные формулы объема [8]. Хотя этот метод прост в выполнении, он страдает от низкой точности измерений [9], отсутствия работы в реальном времени и не может быть применен для прецизионного дифференцированного применения пестицидов. Однако внедрение технологий, таких как ультразвуковые датчики и лидарные датчики для измерения объема кроны [10,11,12,13,14], значительно повысило как точность, так и производительность в реальном времени этих измерений. Юй Лун и др. [15] создали систему обнаружения параметров кроны плодовых деревьев, используя систему определения ориентации, RTK-DGPS и планарный лазерный дальномер. Они применили метод срезов для получения объема кроны, продемонстрировав снижение погрешности по сравнению с ручными измерениями. Ли Цюцзе и др. [16] использовали 2D лидар для сбора данных покадрово для обнаружения деревьев, сегментации и идентификации ствола. Эти данные затем использовались для расчета толщины крон отдельных деревьев, которые дискретизировались на маленькие прямоугольники для получения объема для каждого кадра, с последующим суммированием для вывода общего объема кроны. Ли Пэн и др. [17] предложили метод измерения объема кроны плодового дерева на основе модуля неправильной треугольной призмы. Их метод сегментации неправильной треугольной призмы учитывал пространственное изменение внешнего края кроны, в отличие от метода сегментации прямоугольной призмы. Упомянутые выше исследования успешно решили проблемы низкой точности, связанные с ручными измерениями, и отсутствия работы в реальном времени, тем самым повысив автоматизацию измерения объема кроны. Однако различные методы сегментации, использованные в этих исследованиях, рассматривают крону как сплошной объект, что приводит к погрешностям измерения из-за игнорирования ветвей и пустот внутри кроны плодового дерева [7]. Чжоу и др. [18] разработали модель множественного регрессионного анализа для прогнозирования объема кроны. Эта модель использовала фактические измерения деревьев, вводя высоту кроны и радиус ствола, рассчитанные из облаков точек лидара, для оценки объема кроны. Однако фактические значения кроны были получены из ручных измерений и геометрических аппроксимаций объема, что привело к значительным погрешностям для деревьев с большими внутренними зазорами. Следовательно, обученная модель показала аналогичные неточности для таких типов деревьев. Джеймс П. Андервуд и др. [19] дискретизировали облако точек в кубические вокселы, умножая общее количество на размер воксела для оценки объема кроны. Учитывая, что сканирование лидаром обычно выполняется с одной стороны, они рассчитывали объемы двух половин кроны отдельно и суммировали их для получения общего объема кроны. Хотя этот метод отличается высокой точностью, он становится вычислительно сложным при работе с большими объемами данных облака точек, что делает обнаружение объема кроны в реальном времени трудным и ограничивает его применение в прецизионном опрыскивании.
В прецизионном дифференцированном применении пестицидов объем кроны существенно влияет как на регулирование ветра, так и на объем применения пестицидов. Однако существующие методы измерения объема кроны часто упускают из виду зазоры в кроне, что приводит к существенным погрешностям измерения и недостаточной производительности в реальном времени, что делает их непригодными для применения в реальном времени для прецизионного дифференцированного применения пестицидов в садах. Для решения этих проблем в данном исследовании разрабатывается модель измерения объема кроны с использованием данных облака точек лидара. Входные признаки, используемые в модели, включают количество точек в облаке, 2D-контур облака точек в направлении проекции X, 2D-контур облака точек в направлении проекции Z, 2D-ширину в направлении проекции Y и 2D-длину в направлении проекции Z. Объем кроны, полученный методом интегрирования объема по сетке, служит выходной переменной. Оптимизация гиперпараметров проводится для регрессии на основе метода частичных наименьших квадратов (PLSR), нейронных сетей с обратным распространением ошибки (BP) и градиентного бустинга деревьев решений (GBDT) с использованием набора данных из этого исследования. Модели строятся с использованием оптимальных гиперпараметров для обеспечения поддержки точной модели измерения объема кроны для регулирования ветра и контроля дозировки в технологии прецизионного дифференцированного применения пестицидов.
2. Материалы и методы
2.1. Сбор данных облака точек
2.1.1. Экспериментальная платформа
В данной статье используется колесный трактор LZY604 (производитель: Shandong Weifang Luzhong Tractor Co., Вэйфан, Китай), оснащенный функцией автономного вождения, для сбора данных облака точек лидара с кроны плодового дерева. Трактор оборудован 16-лучевой лидарной системой, схема установки показана на Рисунке 1. Высота установки составляет 205 см, лидарная система имеет горизонтальный угол обзора 360°, точность измерения ±2 см, частоту вращения, установленную на 10 Гц, и разрешение по горизонтальному углу 0,2°. Трактор работает со скоростью движения 3,6 км/ч.
Рисунок 1. Беспилотный колесный трактор LZY604.
2.1.2. Сбор данных облака точек лидара плодовых деревьев
Место сбора облака точек расположено в саду Цзиньнюшань, город Тайань, провинция Шаньдун (116°94′~116°97′ в.д., 36°13′~36°36′ с.ш.). Этот регион относится к зоне умеренно-теплого полусухого муссонного климата. В саду в основном культивируют яблони Фудзи с использованием системы плотной посадки на карликовом подвое. Расстояние между рядами плодовых деревьев составляет 4 м, между растениями в ряду — 3 м, всего было отобрано 121 дерево. Собранные образцы эффективно отражают текущее состояние роста разновидностей плодовых деревьев на экспериментальном поле. Процесс сбора облака точек показан на Рисунке 2, измерения записаны в метрах (м).
Рисунок 2. Сбор данных облака точек. (a) Место сбора. (b) Изображение облака точек с нескольких ракурсов.
2.2. Предварительная обработка данных облака точек
2.2.1. Устранение шума в облаке точек
В процессе фактического сбора данных облака точки различные факторы, такие как вибрации от трактора, ветер в окружающей среде и собственные характеристики плодовых деревьев, могут вносить неизбежный шум в данные облака точек. Эти шумовые точки увеличивают объем данных облака точек, что может негативно повлиять на точность моделирования и извлечения информации. Распространенные техники устранения шума в облаке точек включают медианную фильтрацию [20], усредняющую фильтрацию [21], фильтрацию по Гауссу [21], двустороннюю фильтрацию [22] и статистическое удаление выбросов (SOR) [23]. Среди этих методов фильтрация по Гауссу и усредняющая сглаживают данные для устранения шума, но могут вызывать искажение краев, что делает их непригодными для данного исследования, поскольку граничные профили являются критически важными признаками. Медианная фильтрация предполагает равномерное распределение данных, что делает ее менее гибкой при обработке областей с вариациями плотности, таких как края или разреженные точки. Двусторонняя фильтрация имеет сложные параметры, что затрудняет достижение надлежащего баланса между сглаживанием и сохранением краев. В отличие от них, SOR основан на статистическом анализе и оценивает, является ли точка выбросом, путем расчета среднего расстояния между точкой и ее соседними точками. Эта техника эффективно удаляет точки, которые значительно отклоняются от распределения данных, без сглаживания, тем самым сохраняя информацию о краях и деталях. Кроме того, SOR хорошо сохраняет характеристики данных облака точек как в разреженных, так и в плотных областях, и ее простой принцип делает ее подходящей для набора данных, используемого в этом исследовании. В данном исследовании применяется техника статистического удаления выбросов (SOR) для устранения выбросов из данных облака точек. Конкретные шаги следующие:
Для расчета среднего расстояния от каждой точки до ее K ближайших соседей значение K должно определяться на основе масштаба данных и плотности облака точек. После проведения нескольких испытаний было обнаружено, что оптимальные результаты достигаются при значении K, равном 20.
Расчет глобального среднего и стандартного отклонения средних расстояний для всех точек в наборе данных.
Установив порог расстояния с использованием глобального среднего и стандартного отклонения, порог затем сравнивается со средним расстоянием каждой точки. Точки, превышающие этот порог, отмечаются как выбросы и впоследствии удаляются из набора данных.
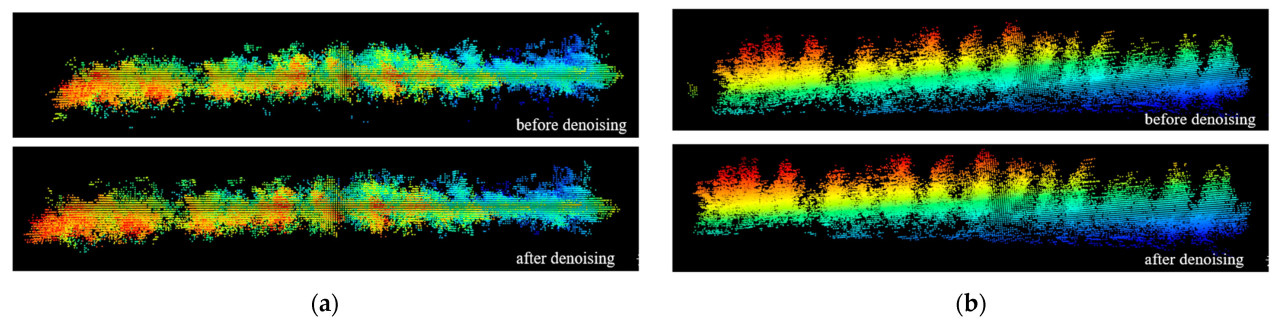
Сравнение техники устранения шума статистическим удалением выбросов (SOR) до и после применения представлено на Рисунке 3. На Рисунке 3a сравнение вида сверху показывает, что техника SOR эффективно удалила выбросы с фона, значительно снизив влияние шума на последующую обработку. Рисунок 3b демонстрирует, что техника SOR оказывает минимальное воздействие на профиль кроны, эффективно сохраняя информацию о краях и деталях, тем самым обеспечивая полноту и надежность последующей обработки профиля кроны.
Рисунок 3. Сравнение до и после устранения шума фильтром SOR. (a) Вид сверху до и после устранения шума. (b) Вид спереди до и после устранения шума.
2.2.2. Извлечение целевой области
Данные облака точек содержат значительное количество фоновых точек, не связанных с плодовыми деревьями, что увеличивает сложность последующей обработки. Поскольку точное применение нацелено на отдельные плодовые деревья, важно получать параметры для каждого плодового дерева на основе данных облака точек лидара. Для достижения этого используется программное обеспечение CloudCompare (2.13.1) для ручной сегментации облака точек. Процесс начинается с обрезки с вида спереди, за которым следует тщательная проверка под разными углами, включая вид сверху и сбоку, чтобы обеспечить точность полученных данных облака точек для одного плодового дерева. Рисунок 4 иллюстрирует схематическое представление облака точек для одного плодового дерева после процесса обрезки.
Рисунок 4. Облако точек отдельных плодовых деревьев.
2.3. Получение признаковой информации из данных облака точек
2.3.1. Извлечение контурной линии границы кроны
Алгоритм альфа-форм (alpha shapes), предложенный Х. Эдельсбреннером [24], представляет собой простой и эффективный метод быстрого извлечения граничных точек. Для любой формы плоского облака точек контурные точки образуются траекторией окружности радиусом a, когда она катится вокруг облака точек. Однако алгоритм альфа-форм может обнаруживать контурные точки только в двумерных облаках точек. Поэтому для извлечения контурных точек облака точек, расположенных по прямой линии, точки должны быть спроецированы на двумерную плоскость, обычно плоскость XOY.
Трехмерное облако точек состоит из набора неупорядоченных точек в 3D-пространстве, которые могут быть спроецированы на любую 2D-плоскость для получения 2D-видов и связанной с ними признаковой информации. Трехмерные плоскости представлены единообразно следующим образом:
где 𝑎, 𝑏 и 𝑐 представляют нормальные векторы плоскостей X, Y и Z соответственно, которые определяют ориентацию плоскости; d — это отрицательное значение расстояния от плоскости до начала координат, определяющее смещение плоскости. Поскольку в данном исследовании проецирование выполняется на плоскости X, Y и Z, значение d установлено равным 0. Например, когда плоскость проекции ориентирована в направлении Z (XOY), значения 𝑎, 𝑏 и 𝑐 равны 0, 0 и 1 соответственно, и аналогичные значения применяются для других направлений проекции.
Предполагая, что (𝑥0,𝑦0,𝑧0) и (𝑥2,𝑦2,𝑧2) — две точки на плоскости, подстановка в Уравнение (1) дает:
(𝑥1−𝑥2,𝑦1−𝑦2,𝑧1−𝑧2) — вектор в плоскости, и согласно приведенному выше уравнению, (𝑎,𝑏,𝑐) перпендикулярен этому вектору, т.е. (𝑎,𝑏,𝑐) является нормалью к плоскости.
Предположим, (𝑥0,𝑦0,𝑧0) — любая точка в пространстве, имеющая проекционные координаты (𝑥,𝑦,𝑧) в плоскости, и вектор, состоящий из этих двух точек. То есть, предполагая нормальный вектор плоскости, тогда вектор должен быть параллелен нормальному вектору (𝑎,𝑏,𝑐), таким образом получая:
где t — расстояние, на которое точка (𝑥0,𝑦0,𝑧0) перемещается вдоль направляющего вектора (a, b, c).
Параметрические выражения для уравнений прямой следующие:
Подстановка приведенных выше результатов в уравнение плоскости Уравнение (1) дает:
Подставьте Уравнение (5) обратно в Уравнение (4), чтобы получить координаты после проекции и прочитать облако точек после проекции, как показано на Рисунке 5 проекция плоскости 3D-облака точек.
Рисунок 5. Проекция плоскости трехмерного облака точек. (a) Проекция на ось X. (b) Проекция на ось Y. (c) Проекция на ось Z.
Рисунок 6 представляет сравнение между стандартным алгоритмом извлечения контура Alpha Shape и улучшенным алгоритмом извлечения контура Alpha Shape по направлениям проекции X, Y и Z. Стандартный алгоритм извлечения контура Alpha Shape [25] сначала проводит триангуляцию Делоне на 2D-облаке точек, а затем проходит по каждому ребру всех треугольников, чтобы оценить его валидность. Формула для определения двух возможных позиций центров окружностей, определяемых конечными точками ребра и фиксированным радиусом, следующая:
где 𝑐 — центр окружности; m — центроид ребра; 𝑟 — радиус окружности, 1/alpha, alpha = 1,95; 𝐿 — длина ребра; и n — нормальный вектор ребра.
Рисунок 6. Треугольное сечение и построение окружности по ребру.
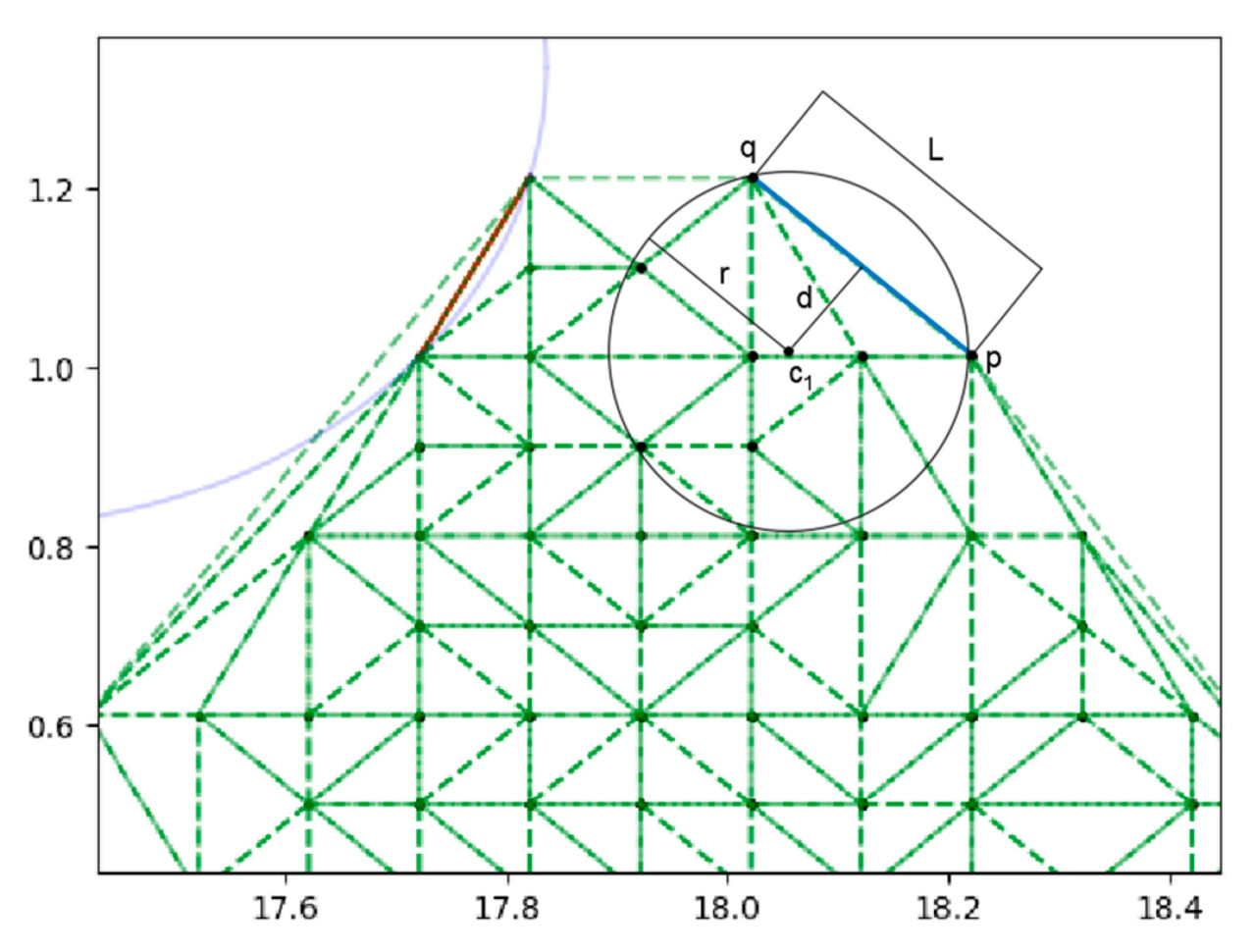
KD Tree используется для запроса количества облаков точек в радиусе r от двух местоположений центров окружностей. Отрезок линии считается валидным, если количество соседних точек, возвращаемое запросом KD Tree, меньше или равно 2 для любого заданного центра окружности; в противном случае он считается невалидным. В практических применениях контур плотного облака точек и его форма могут приводить к ситуациям, когда количество точек вокруг окружности контурной линии превышает 2. Описанный выше метод оценки не способен идентифицировать эту часть границы. Как показано на Рисунке 6, контурная линия представляет треугольное сечение, с окружностью, проведенной вокруг его ребра. Хотя этот отрезок линии представляет граничный контур, окружность отрезка линии содержит 6 точек, что приводит к его неправильной классификации как неграничного контура. Следовательно, окончательное вычисленное значение для фактического контура занижено, что приводит к значительной погрешности.
Учитывая упомянутые проблемы, данная статья улучшает алгоритм извлечения контура Alpha Shape, в основном фокусируясь на оценке валидности границы после треугольного сечения. Улучшение использует метод векторного произведения, который включает умножение двух векторов на результаты их положительных и отрицательных знаков. Этот подход определяет, расположена ли каждая соседняя точка внутри окружности на той же стороне, что и две конечные точки ребра и центр окружности. Формула следующая:
где 𝑃 и 𝑄 — две конечные точки боковой линии, с координатами (𝑥𝑝,𝑦𝑝), (𝑥𝑞,𝑦𝑞); 𝑐1 — центр окружности, с координатами (𝑥𝑐,𝑦𝑐). Два результата векторного произведения с одинаковым знаком указывают, что соседняя точка расположена на той же стороне ломаной линии P−c1−Q. Для граничной линии с более чем двумя точками внутри окружности, если все соседние точки расположены на одной стороне ломаной линии P−c1−Q, граничная линия считается валидным контурным краем.
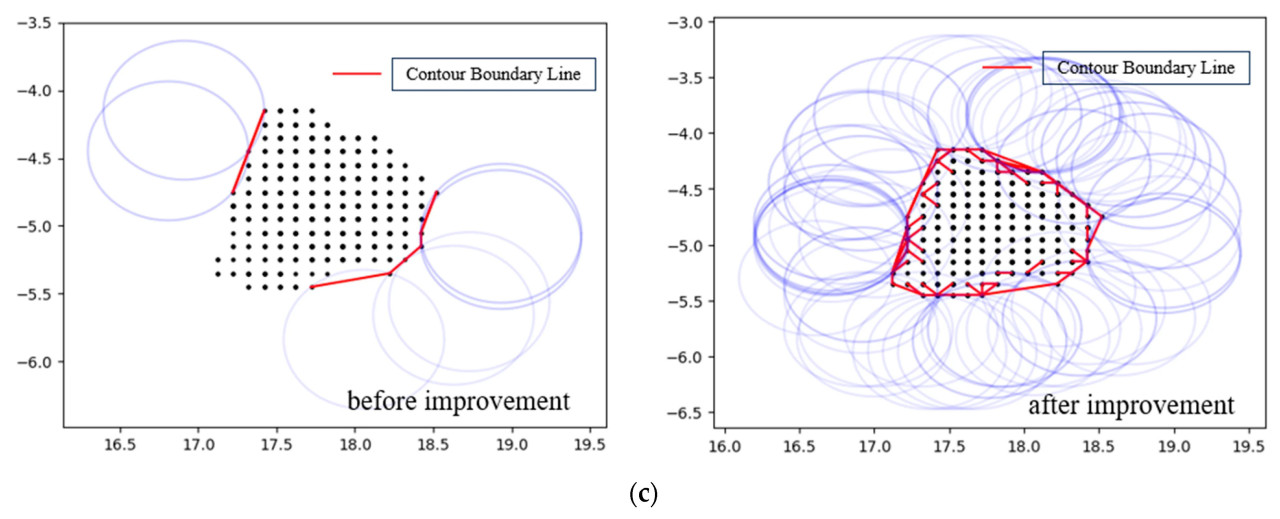
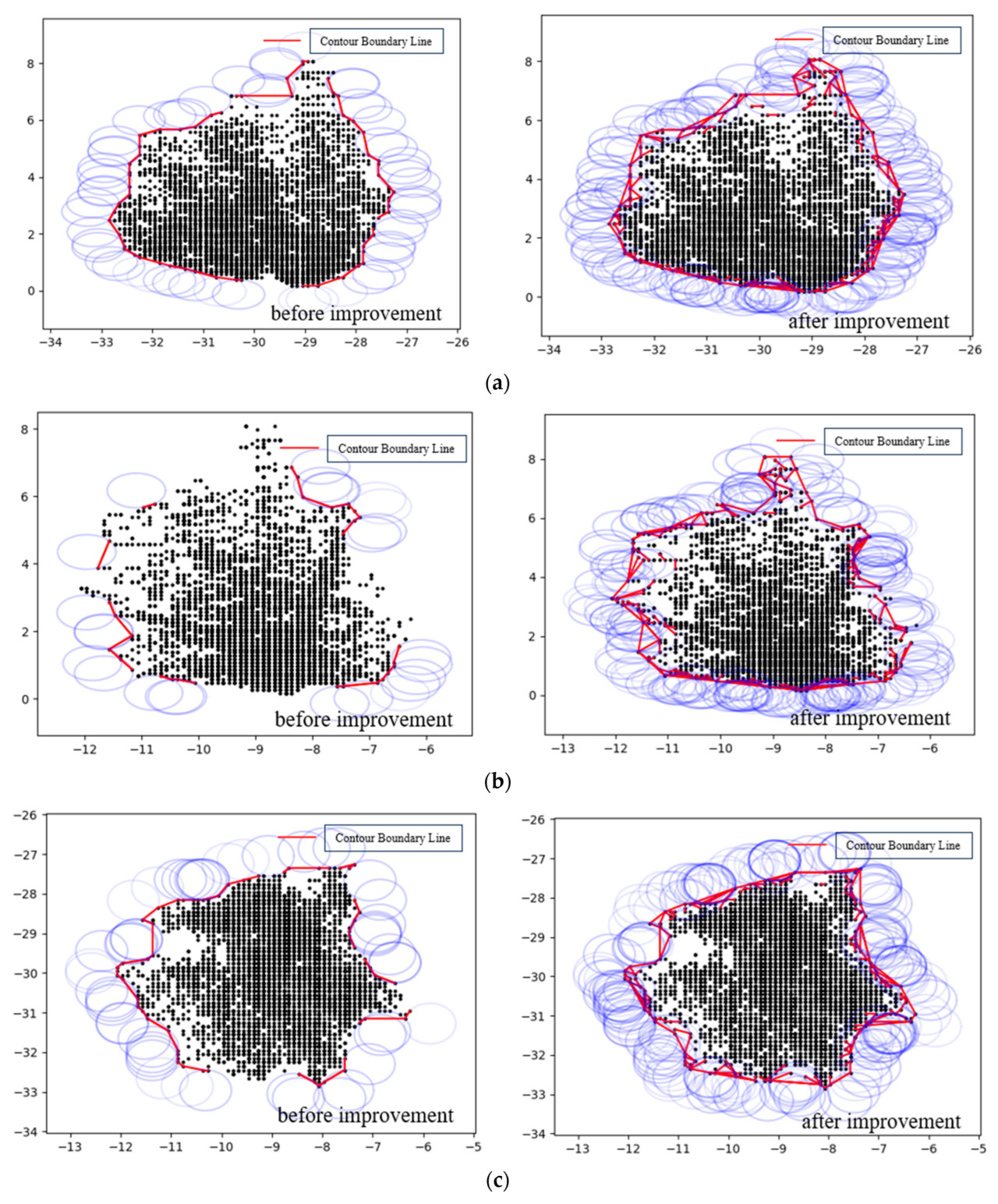
Сравнение алгоритма извлечения контура Alpha Shape до и после улучшения проиллюстрировано на Рисунке 7. Неулучшенный алгоритм извлечения контура Alpha Shape показывает значительное отклонение от фактического контура и отсутствие регулярности. В отличие от этого, улучшенный алгоритм извлечения контура Alpha Shape эффективно снижает случаи, когда фактические границы ошибочно классифицируются как неграничные. Однако все еще присутствуют случаи, когда неграничные точки ошибочно идентифицируются как границы.
Рисунок 7. Контурные линии двумерного облака точек. (a) Сравнение контуров в направлении проекции X; (b) Сравнение контуров в направлении проекции Y; (c) Сравнение контуров в направлении проекции Z.
В ответ на упомянутые проблемы, истинное значение подгоняется к значению, полученному алгоритмом, чтобы достичь более точной длины контурной границы. Истинное значение определяется с помощью анализа в программном обеспечении CAD (2022), и соответствующая формула анализа следующая:
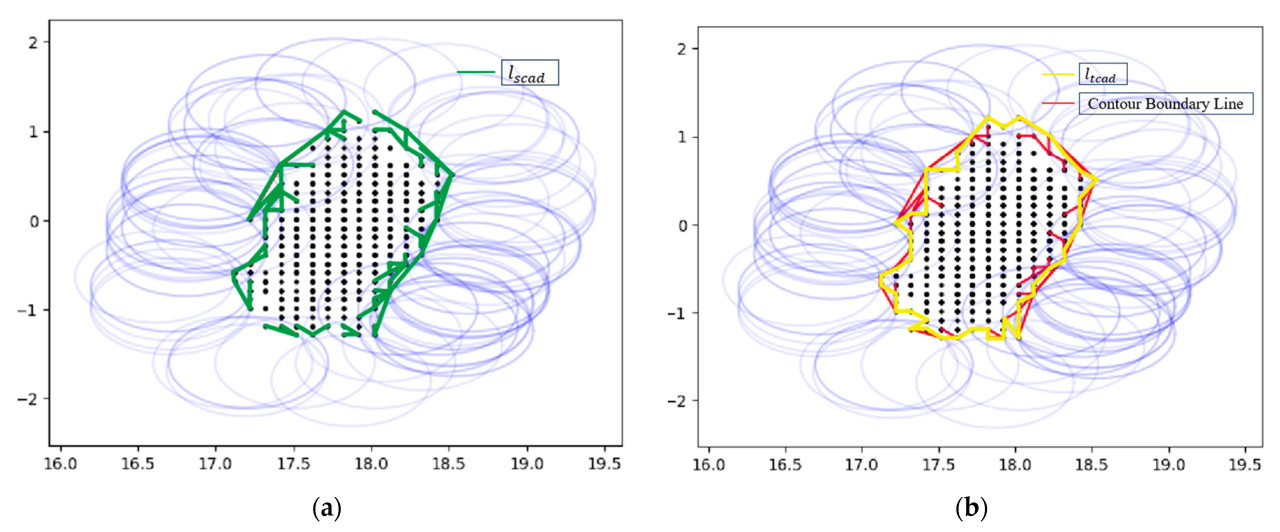
где 𝑙𝑠𝑐𝑎𝑑 — длина, вручную отмеченная в SolidWorks алгоритмом извлечения контура Alpha Shape, 𝑙𝑠 — длина контура, полученная алгоритмом извлечения контура Alpha Shape, которая имеет большую погрешность, 𝑙𝑡𝑐𝑎𝑑 — длина фактического края, вручная отмеченная в CAD, и 𝑙𝑡 — длина реального контура, которая является более точной, в то время как 𝑙𝑠𝑐𝑎𝑑, 𝑙𝑡𝑐𝑎𝑑 показаны на Рисунке 8. Аппроксимация 𝑙𝑡 и 𝑙𝑠 в программном обеспечении SPSSAU дала следующие уравнения:
Рисунок 8. Сравнение длин, полученных ручной разметкой алгоритма извлечения контура Alpha Shape, с длинами фактического контура. (a) Длины, полученные ручной разметкой алгоритма извлечения контура Alpha Shape. (b) Ручная разметка длин фактического контура.
2.3.2. Получение объема кроны
Метод интегрирования по сетке [26] — это простой подход для оценки объема облака точек. Основная концепция заключается в проецировании 3D-облака точек на 2D-плоскость и разделении этой плоскости на несколько регулярных сеток. Для каждой сетки рассчитывается вертикальное расстояние между самой высокой и самой низкой точками статистических данных облака точек, представляющее разность высот. Эта разность высот затем умножается на площадь сетки, чтобы получить приблизительный объем каждой сетки. Наконец, путем суммирования объемов всех сеток определяется общий объем объекта, представленного облаком точек.
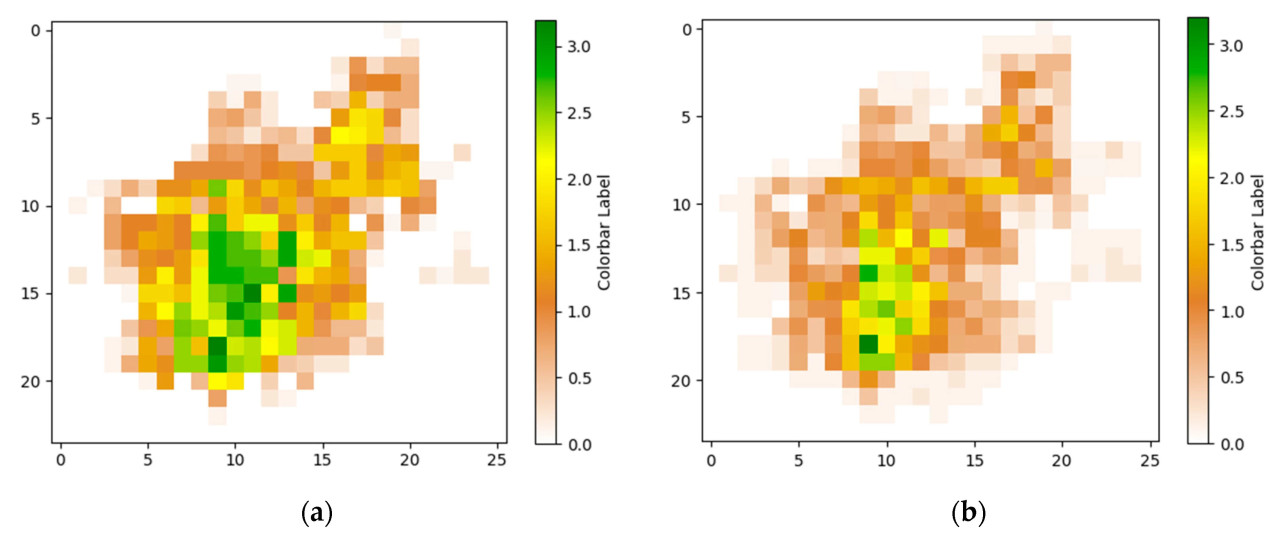
Процесс расчета объема методом интегрирования по сетке не учитывал возможные зазоры внутри высоты сетки. Разность высот непосредственно определялась самыми высокими и самыми низкими точками, предполагая непрерывность высоты. Однако фактическая крона дерева содержит множество зазоров и часто является прерывистой, что приводит к значительным погрешностям в расчетах объема из-за этих упущений. В этом исследовании мы экспериментировали с разными размерами сетки и сравнили результаты, в конечном итоге определив оптимальный размер сетки как 0,11 м. Чтобы решить проблемы метода интегрирования по сетке, мы улучшили расчет разности высот, введя порог на основе размера сетки, установленный на три раза больше размера сетки (0,33 м). Разности высот между двумя точками со значением Z, превышающим порог, классифицируются как зазоры и исключаются из интегрирования объема. Обычно центральная область кроны дерева густо разветвлена, в то время как внешняя область имеет редкую листву, что приводит к большим разностям высот в центре и меньшим — на периферии. Рисунок 9 иллюстрирует сравнение распределений разностей высот кроны между стандартным методом интегрирования объема по сетке и улучшенным методом. Анализ показывает, что распределение разностей высот, полученное улучшенным алгоритмом, более точно соответствует фактическим условиям. Однако улучшенный метод интегрирования объема по сетке требует обширных операций с сеткой, фильтрации по маске и сортировки, что приводит к более длительному времени выполнения и значительным требованиям к памяти для хранения промежуточных результатов расчетов облака точек. Эта сложность создает проблемы для приложений в реальном времени в садовом опрыскивании. Поэтому результаты объема, полученные улучшенным методом интегрирования объема по сетке, используются в качестве меток для прогнозирования объема в модели машинного обучения, способствуя разработке точной и эффективной модели измерения объема кроны в реальном времени для прецизионного опрыскивания.
Рисунок 9. Сравнение метода интегрирования объема по сетке до и после улучшения. (a) Метод интегрирования объема по сетке до улучшения. (b) Улучшенный метод интегрирования объема по сетке.
Поскольку крона плодового дерева представляет собой неправильную трехмерную структуру, ее общая пространственная морфология не может быть точно описана математической моделью. Дополнительно, процесс ручного измерения не учитывает влияние пустот, что делает невозможным прямое определение теоретического значения объема кроны. Вэй Сюэхуа и др. [27] предложили метод моделирования объемными элементами, который включает расчет объема кроны с использованием объемных элементов со стороной 0,2 м. Сравнительный анализ традиционных методов расчета объема кроны пришел к выводу, что метод моделирования объемными элементами является более точным и объективным. Поэтому данная статья основывается на методе моделирования объемными элементами, используя размеры объемных элементов 0,15 м и 0,1 м при оценке результатов, чтобы служить теоретическими ориентирами для оценки точности получения объема. Кроме того, было случайным образом отобрано 30 образцов для анализа точности.
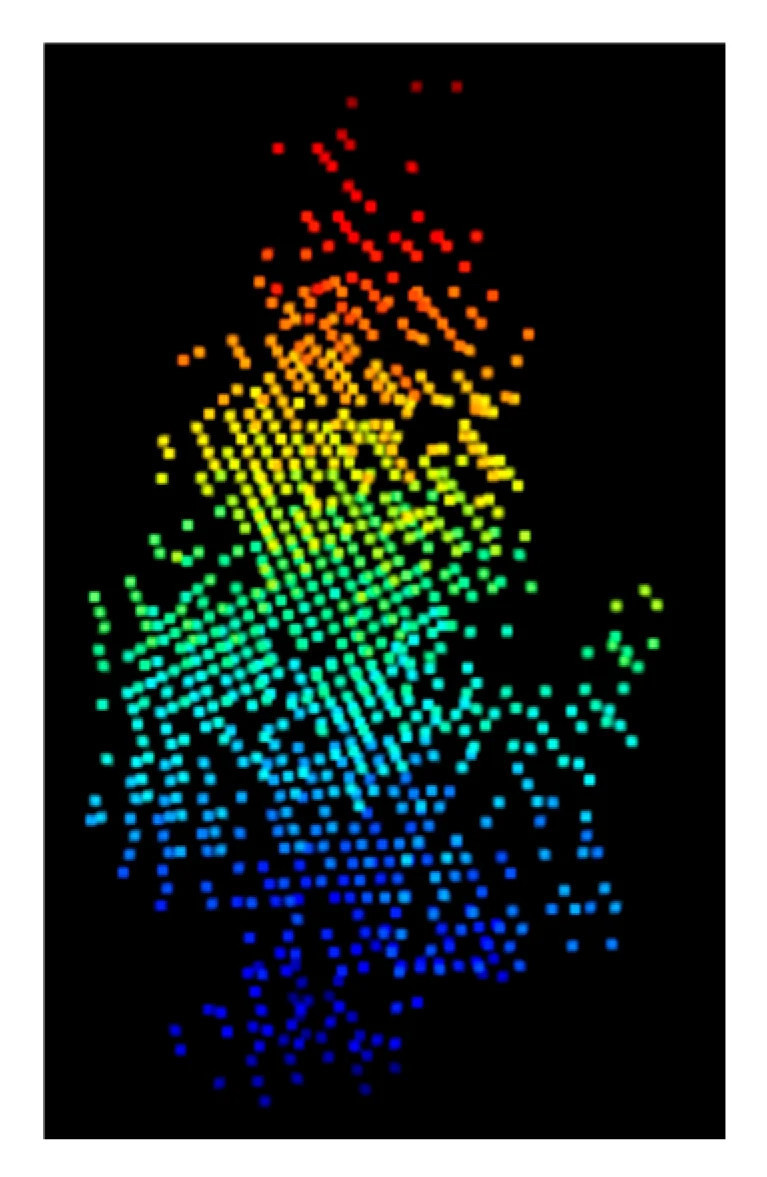
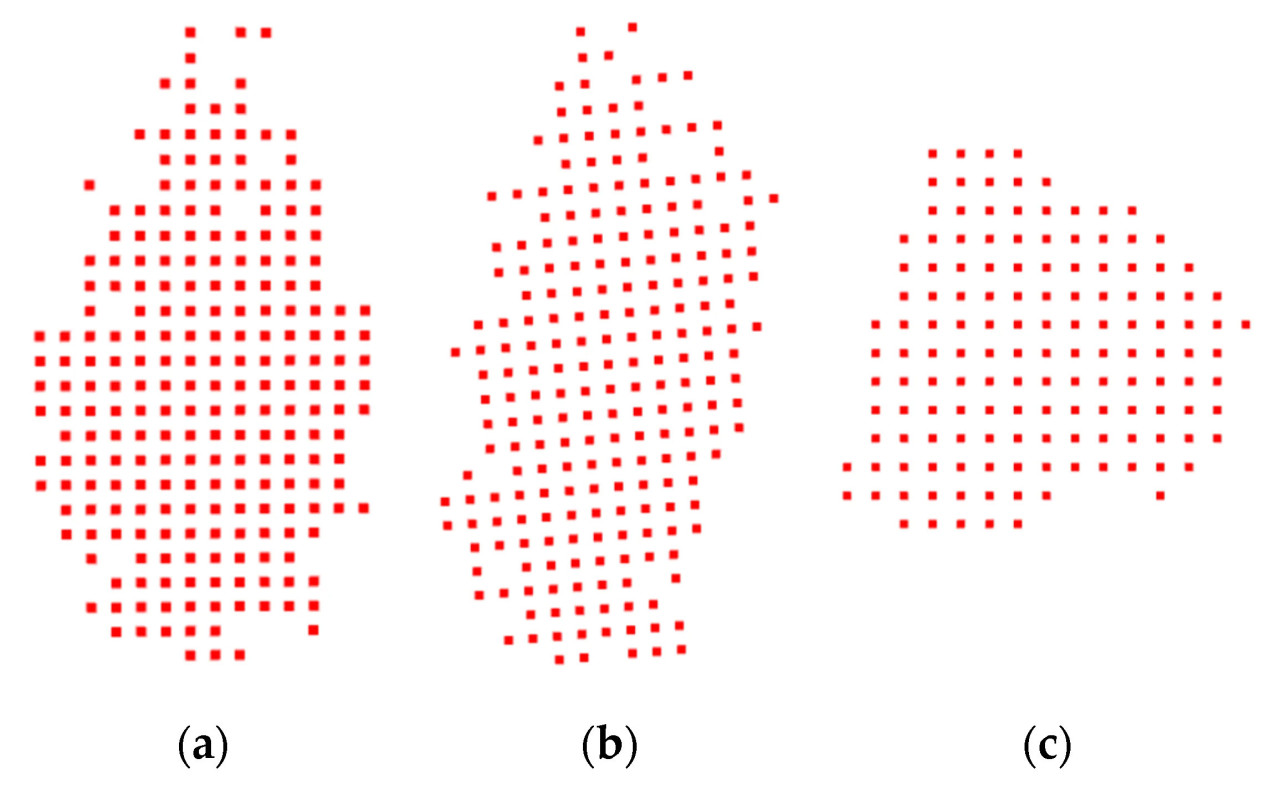
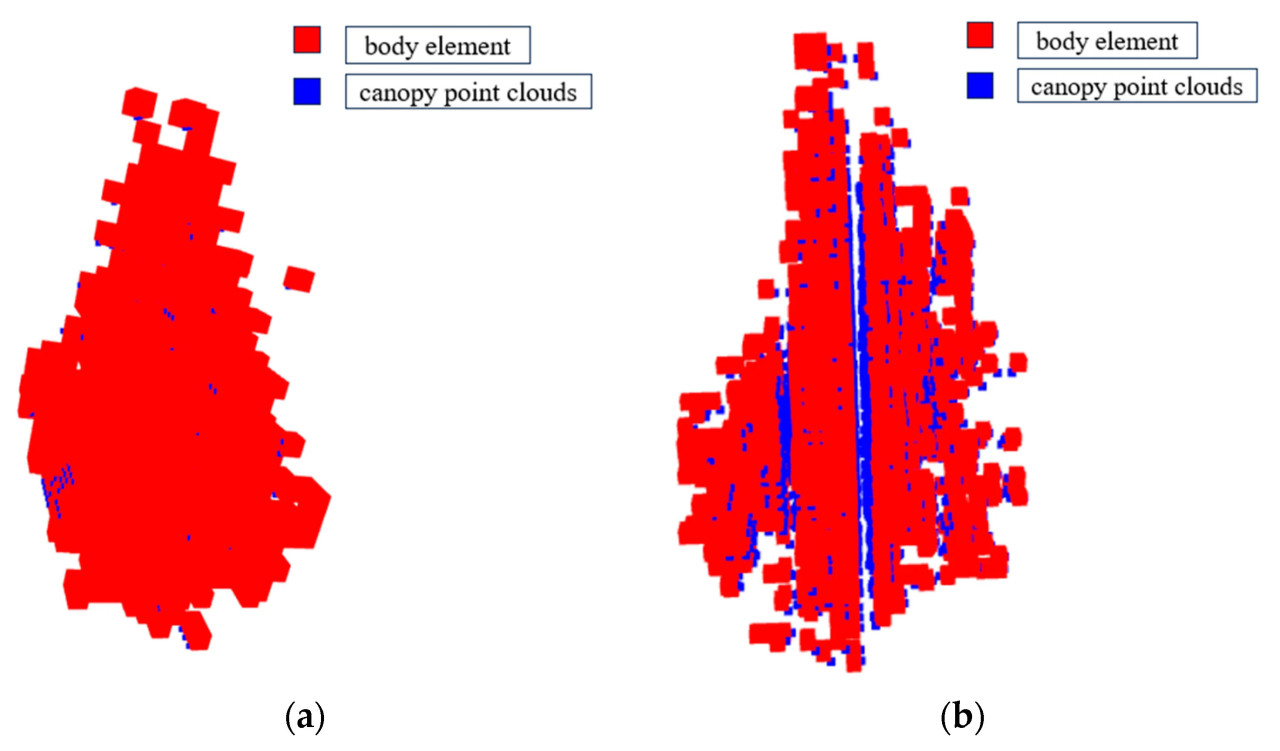
Как показано на Рисунке 10, на котором отображен объемный элемент кроны вместе с представлением облака точек, красные квадраты представляют объемные элементы, а синие точки обозначают облака точек кроны. Рисунок 10a представляет отображение объемного элемента и облака точек для кроны с размером объемного элемента 0,15 м. В этом случае объемный элемент по существу охватывает все облака точек внутри кроны; однако он также включает в себя все внутренние зазоры, что теоретически приводит к завышению измеренного объема. Напротив, Рисунок 10b изображает представление объемного элемента и облака точек для кроны с размером объемного элемента 0,1 м. Здесь объемный элемент не охватывает все облака точек в кроне, оставляя несколько значительных зазоров внутри кроны, которые явно не являются типичными для обычных зазоров кроны. Следовательно, измеренный объем теоретически занижен.
Рисунок 10. Диаграммы представления объемного элемента и облака точек. (a) Размер объемного элемента принят за 0,5 м. (b) Размер объемного элемента принят за 0,1 м.
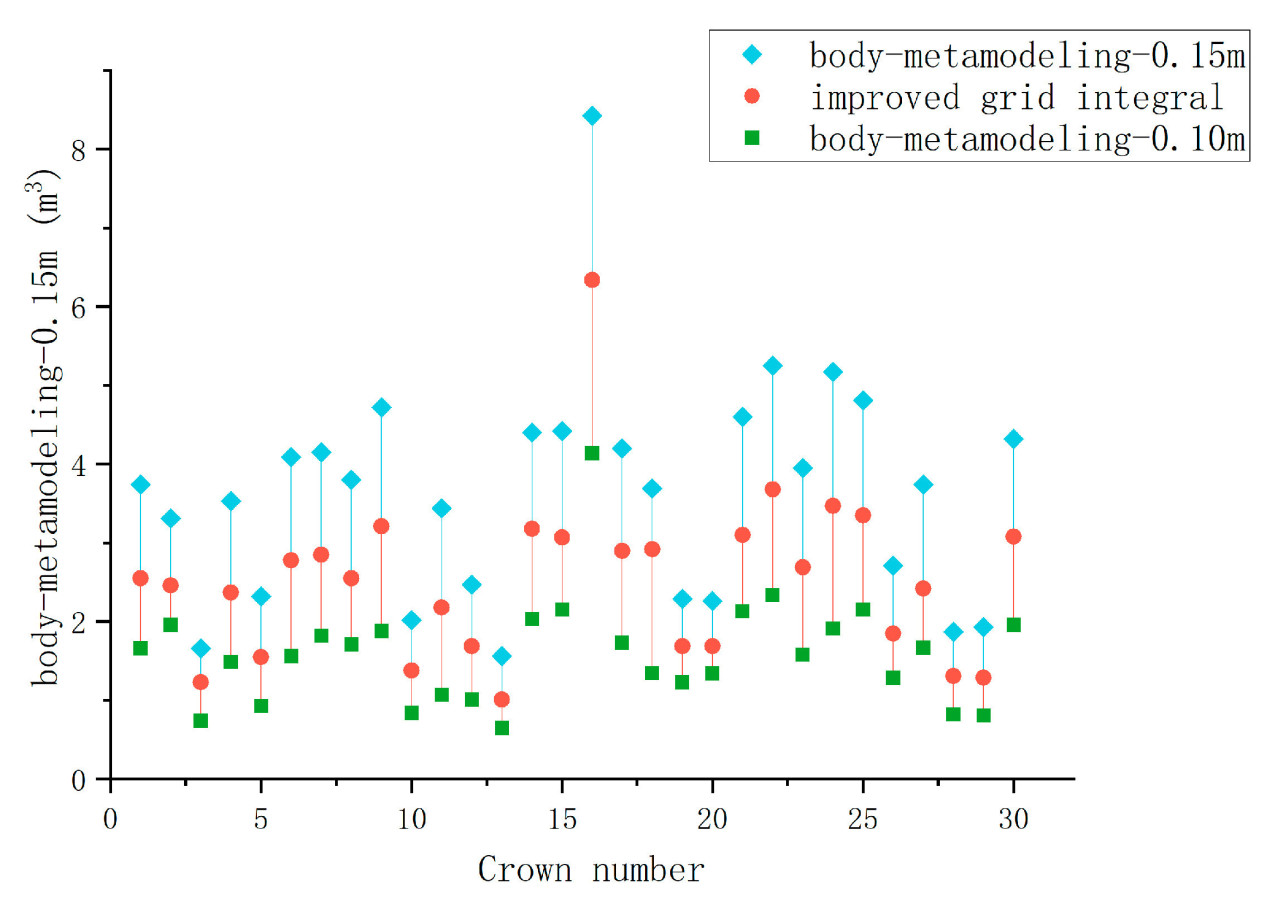
Из Рисунка 11 видно, что колебания объема по методу моделирования объемными элементами и улучшенному методу интегрирования по сетке в значительной степени согласуются, демонстрируя высокую степень соответствия. Это сходство возникает из-за того, что оба метода измерения объема разделяют одни и те же фундаментальные принципы, с основной разницей в их учете пустот. В методе моделирования объемными элементами, когда размер объемного элемента установлен на 0,15 м, он охватывает пустоты внутри кроны, что приводит к завышенному измерению объема. Напротив, когда размер объемного элемента уменьшен до 0,1 м, он не охватывает все облако точек, что приводит к уменьшенной оценке объема. Объем, полученный с использованием улучшенного метода интегрирования по сетке в этом исследовании, находится между значениями, полученными методом моделирования объемными элементами для 0,15 м и 0,1 м соответственно. Это наблюдение согласуется с анализом, учитывающим пустоты, указывая, что точность измерения относительно выше.
Рисунок 11. Сравнение результатов между методом объемных элементов и улучшенным методом интегрирования по сетке.
2.4. Отбор признаков
Отбор признаков — это важнейший аспект проектирования признаков, фокусирующийся на идентификации оптимального подмножества признаков при одновременном устранении нерелевантных или избыточных. Этот процесс не только уменьшает общее количество признаков, но и повышает точность модели и сокращает время выполнения [28]. Отбор признаков может быть классифицирован на три категории: методы фильтрации, методы обертки и встроенные методы [29]. Методы фильтрации оценивают отдельные признаки на основе их дисперсии или релевантности, устанавливая порог или выбирая определенное количество признаков для фильтрации. Однако эти методы обычно полагаются на статистические свойства (например, корреляцию, дисперсию) и могут упускать из виду сложные закономерности и взаимосвязи между признаками, потенциально приводя к пропуску важных признаков. Методы обертки оценивают релевантность признаков через производительность модели, учитывая взаимодействия между признаками, что позволяет улавливать более сложные взаимосвязи. Они могут автоматически определять оптимальное количество признаков с помощью перекрестной проверки, хотя это влечет значительные вычислительные затраты. Встроенные методы интегрируют отбор признаков в процесс построения модели, используя внутренние характеристики модели. Однако этот подход сильно зависит от производительности выбранной модели, что может привести к субоптимальному отбору признаков, если модель выбрана плохо. Учитывая относительно небольшое количество признаков в данном исследовании, ожидается, что метод обертки будет работать лучше; поэтому данная статья выбирает подход обертки.
Метод рекурсивного исключения с перекрестной проверкой (RFE-CV) интегрирует технику рекурсивного исключения с перекрестной проверкой, где метод рекурсивного исключения служит подходом обертки, который использует последовательный выбор и обратный поиск [30]. Конкретные шаги включают выбор базовой модели, обучение модели, систематическое исключение неважных признаков и оценку производительности модели с использованием перекрестной проверки в качестве метрики до тех пор, пока не будет определено оптимальное количество признаков. RFE-CV широко используется, демонстрирует хорошую стабильность и эффективно улавливает сложные взаимосвязи между признаками.
Цель фазы отбора признаков — идентифицировать подмножество признаков, которые сильно коррелируют с целевой переменной, без необходимости учитывать конкретные предположения, сделанные последующими моделями относительно взаимосвязей признаков. Случайные леса делают меньше предположений об этих взаимосвязях и обладают высокой устойчивостью, фокусируясь исключительно на идентификации важных признаков на фазе отбора, не предполагая, что взаимосвязи между этими признаками являются линейными или нелинейными. Поэтому данная статья выбирает случайный лес в качестве базовой модели для рекурсивного исключения.
Набор данных, использованный в этом исследовании, был введен в метод RFE-CV в сочетании с моделью Random Forest для оценки следующих десяти признаков: количество точек в облаке точек, 2D-контур облака точек в направлении проекции X, 2D-контур облака точек в направлении проекции Y, 2D-контур облака точек в направлении проекции Z, 2D-длина облака точек в направлении проекции X, 2D-ширина облака точек в направлении проекции Y, 2D-длина облака точек в направлении проекции Z, 2D-плотность облака точек в направлении проекции X, 2D-плотность облака точек в направлении проекции Y и 2D-плотность облака точек в направлении проекции Z.
Алгоритм рекурсивного исключения признаков с перекрестной проверкой на основе случайных лесов идентифицирует пять важных признаков: количество точек в облаке точек, 2D-контур облака точек в направлении проекции X, 2D-контур облака точек в направлении проекции Z, 2D-ширина облака точек в направлении проекции Y и 2D-длина облака точек в направлении проекции Z.
2.5. Построение модели для измерения объема кроны
На практике наиболее подходящая модель для каждой исследуемой области не является уникальной, и не существует единой оптимальной модели машинного обучения [31]. Поэтому при обучении моделей измерения объема кроны с использованием машинного обучения необходимо учитывать проверку применимости модели. Учитывая изменчивость характеристик данных, данная статья выбирает три различных типа моделей — регрессию на основе метода частичных наименьших квадратов (PLSR), нейронные сети с обратным распространением ошибки (BP) и градиентный бустинг деревьев решений (GBDT) — которые могут адаптироваться к широкому спектру наборов данных для обучения и оценки. Это исследование всесторонне анализирует производительность этих моделей на текущем наборе данных, чтобы определить оптимальную модель для измерения объема кроны.
2.5.1. Построение модели измерения объема кроны на основе регрессии методом частичных наименьших квадратов
Модель регрессии на основе метода частичных наименьших квадратов (PLSR) [32,33] — это метод, который интегрирует преимущества анализа главных компонент, канонического корреляционного анализа и множественного линейного регрессионного анализа. Основная идея заключается в идентификации новых главных компонент (ортогональных направлений проекции), которые максимизируют ковариацию между спроецированными зависимыми и независимыми переменными, тем самым устанавливая прогностическую модель. Процесс разработки модели включает следующие шаги: сначала рассчитывается ковариационная матрица независимых и зависимых переменных для извлечения начального набора главных компонент с использованием итеративного алгоритма. Во-вторых, извлеченные главные компоненты рассматриваются как новые независимые переменные, и выполняется линейное регрессионное моделирование зависимой переменной. Наконец, итерация повторяется для извлечения новых главных компонент и выполнения регрессии до тех пор, пока не будет достигнут заранее определенный критерий остановки.
В модели PLSR количество главных компонент является ключевым гиперпараметром. Выбор подходящего количества главных компонент может эффективно сбалансировать сохранение информации и упрощение модели, приводя к улучшению прогностической производительности [34]. Если количество главных компонент слишком низкое, модель может не уловить нюансы вариации данных, что приведет к недообучению. Напротив, если количество слишком велико, модель может включить шум или случайные флуктуации в данных, что приведет к переобучению и увеличению сложности модели. Чтобы решить эти проблемы, в данном исследовании используется метод 10-кратной перекрестной проверки для определения оптимального количества главных компонент. Учитывая, что набор данных содержит всего пять признаков, диапазон для настройки гиперпараметров установлен от 1 до 5 для количества главных компонент.
2.5.2. Построение модели измерения объема кроны на основе нейронной сети BP
Нейронная сеть с обратным распространением ошибки (BP), обычно называемая нейронной сетью BP, представляет собой модель прямой нейронной сети, которая обучается и оптимизируется с использованием алгоритма обратного распространения ошибки [35,36]. В фактическом процессе разработки модели первый шаг включает установку начальных значений для гиперпараметров, таких как скорость обучения, количество нейронов в каждом слое, веса и смещения. Впоследствии выборочные данные подаются в нейронную сеть через входной слой, и выполняются вычисления между слоями до получения окончательного результата. Затем вычисляется ошибка между прогнозируемыми результатами и фактическими результатами, и выполняется обратное распространение ошибки с использованием правила цепочки, которое распространяет ошибку назад по сети от выходного слоя к входному слою. После этого вычисляются градиенты для каждого нейрона на основе ошибки, и обновляются такие параметры, как веса и смещения, при одновременном снижении скорости обучения. Наконец, эти шаги повторяются до достижения максимального количества итераций.
Выбор подходящего количества слоев и нейронов имеет важнейшее значение для производительности модели. Увеличение количества скрытых слоев и нейронов может улучшить способность сети изучать сложные закономерности; однако это также может привести к переобучению и увеличению вычислительной нагрузки. Скорость обучения, которая слишком высока, может вызвать нестабильность обучения и может помешать сходимости, в то время как скорость, которая слишком низка, может привести к медленному процессу обучения и может остановиться до достижения оптимального решения. Дополнительно, коэффициент регуляризации, который слишком велик, может привести к более гладкой модели, помогая избежать переобучения, но может привести к недообучению. Напротив, коэффициент, который слишком мал, может вызвать переобучение. Для оптимизации гиперпараметров нейронной сети BP — таких как количество скрытых слоев, количество нейронов в каждом слое, скорость обучения и коэффициент регуляризации — используется десятикратная перекрестная проверка [37].
Основываясь на сложности набора данных, был выбран соответствующий диапазон гиперпараметров для модели нейронной сети BP. Конкретные диапазоны для гиперпараметров следующие: количество скрытых слоев и нейронов в каждом слое включает [32, 64, 128, (32, 32), (64, 64), (64, 32), (128, 64), (128, 32)]; варианты скорости обучения: [0,01, 0,001, 0,0001]; и факторы регуляризации: [0,001, 0,0001, 0,00001]. Учитывая простоту набора данных, выбранные диапазоны гиперпараметров охватывают распространенные настройки, обеспечивая достаточную гибкость для настройки модели с разумными параметрами, подходящими для простых наборов данных. Эти гиперпараметры могут быть свободно скомбинированы в 81 различную конфигурацию, и данное исследование использует стратегию поиска по сетке [38] для оценки производительности различных комбинаций гиперпараметров с помощью перекрестной проверки и идентификации оптимальной комбинации.
2.5.3. Построение модели измерения объема кроны на основе градиентного бустинга деревьев решений
Градиентный бустинг деревьев решений (GBDT) — это продвинутая модель ансамблевого обучения, построенная на основе алгоритма CART [39]. В процессе разработки модели GBDT сначала создается начальная прогностическая модель. На каждой итерации вычисляются остатки предыдущей модели, и строится новое дерево решений для аппроксимации этих остатков на обучающих данных. Затем вновь обученное дерево решений включается в текущую модель, обычно с регулировкой скорости обучения для контроля его вклада. Посредством множественных итераций новые деревья решений непрерывно добавляются, причем каждая итерация направлена на минимизацию потерь текущей модели и постепенное сближение с оптимальным решением.
Основные гиперпараметры GBDT включают количество деревьев решений, скорость обучения и максимальную глубину деревьев [40]. Для настройки гиперпараметров используется десятикратная перекрестная проверка. Ограниченное количество деревьев решений может неадекватно уловить сложность данных, в то время как избыточное количество может увеличить вычислительную нагрузку и потенциально привести к переобучению. Скорость обучения контролирует вклад каждого дерева решений в окончательный прогноз; меньшая скорость обучения может улучшить точность модели, но требует больше деревьев, тогда как большая скорость обучения может привести к тому, что модель обойдет оптимальное решение во время обучения. Большая максимальная глубина деревьев решений увеличивает их сложность, делая их подходящими для сложных наборов данных, но также может привести к переобучению. Напротив, меньшая глубина может привести к недообучению.
Согласно сложности набора данных, выбран подходящий диапазон гиперпараметров. Конкретные диапазоны гиперпараметров для модели градиентного бустинга деревьев решений следующие: количество деревьев решений: [100, 150, 200, 250, 300]; скорость обучения: [0,01, 0,1, 0,2]; и максимальная глубина деревьев решений: [3, 4, 5]. Всего используется 45 различных комбинаций параметров в стратегии поиска по сетке, которые перекрестно проверяются отдельно, и оптимальные комбинации параметров определяются на основе оценок перекрестной проверки. Выбранные диапазоны гиперпараметров в данной статье охватывают распространенные значения для количества деревьев решений, скорости обучения и максимальной глубины, делая их подходящими для широкого спектра проблем, таким образом эффективно исследуя производительность различных комбинаций моделей.
3. Результаты
Модели PLSR, нейронная сеть BP и GBDT выбраны для оптимальной настройки гиперпараметров. 121 набор данных из набора данных, используемого в этом исследовании, разделен на обучающий набор и тестовый набор в соотношении 7:3. Это соотношение разделения широко применяется в различных проектах машинного обучения [4], гарантируя, что и обучающий набор, и тестовый набор содержат достаточное количество данных, в результате чего получается 45 наборов данных для обучающего набора и 20 наборов данных для тестового набора. Оптимальные комбинации выбранных гиперпараметров используются для аппроксимации выборочных данных через обучающий набор, получая модель множественной регрессии объема кроны. Затем эта модель оценивается с использованием тестового набора для оценки ее окончательной производительности и способности к обобщению. Метрики оценки включают R2 (коэффициент детерминации), RMSE (среднеквадратичная ошибка) и MAE (средняя абсолютная ошибка). Значение R2, которое варьируется от 0 до 1, используется для оценки эффективности аппроксимации модели; чем ближе значение к 1, тем больше способность модели объяснять данные и тем лучше производительность аппроксимации. RMSE и MAE служат мерами ошибки, представляя квадратный корень из квадратов ошибок и среднее абсолютных ошибок между истинными и прогнозируемыми значениями соответственно. В то время как R2 в первую очередь измеряет объясняющую способность модели, RMSE подчеркивает влияние больших ошибок, и MAE обеспечивает интуитивную оценку прогностической точности. Комбинирование этих трех метрик дает всестороннее понимание прогностической производительности модели, способствуя лучшему принятию решений.
3.1. Результаты построения модели измерения объема кроны на основе регрессии методом частичных наименьших квадратов
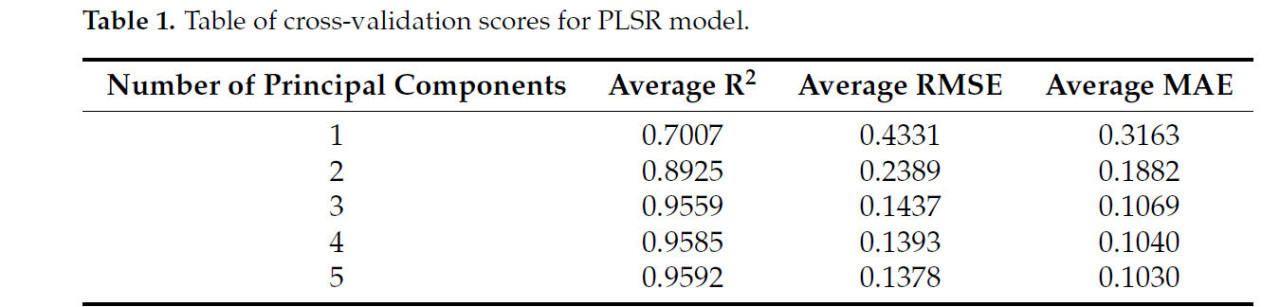
Таблица 1 показывает средние значения R2, RMSE и MAE, полученные с помощью 10-кратной перекрестной проверки для разного количества главных компонент. Когда количество главных компонент установлено на 3, 4 или 5, оценки 10-кратной перекрестной проверки схожи и дают относительно лучшие результаты. Напротив, только с одной главной компонентой среднее значение R2 составляет 0,7007, что приблизительно на 0,25 ниже, чем производительность при оптимальных гиперпараметрах. Этот результат подчеркивает важность настройки гиперпараметров в модели регрессии методом частичных наименьших квадратов (PLSR).
Таблица 1. Таблица оценок перекрестной проверки для модели PLSR.
Модели обучались с количеством главных компонент 3, 4 и 5 соответственно, и тестовый набор использовался для оценки окончательной производительности модели. С тремя главными компонентами тестовый набор модели PLSR достиг R2 0,9742, RMSE 0,1879 и MAE 0,1161. С четырьмя главными компонентами тестовый набор модели PLSR дал R2 0,9739, RMSE 0,1892 и MAE 0,1228. Наконец, с пятью главными компонентами тестовый набор модели PLSR показал R2 0,9737, RMSE 0,1898 и MAE 0,1229.
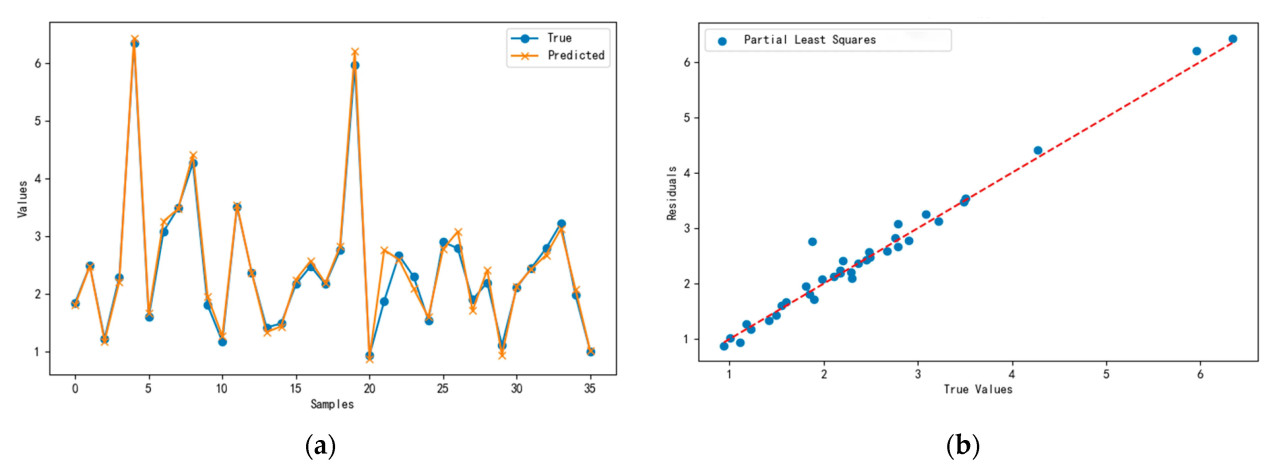
Сравнительный анализ результатов обучения модели регрессии методом частичных наименьших квадратов (PLSR) с разным количеством главных компонент показывает, что результаты перекрестной проверки довольно схожи, когда количество главных компонент установлено на 3, 4 и 5. Однако результаты тестового набора, включая R2, RMSE и MAE, указывают на небольшое преимущество обученной модели измерения объема кроны, когда количество главных компонент установлено на 3. Учитывая относительную простоту модели с тремя главными компонентами, данное исследование выбирает 3 в качестве оптимального гиперпараметра для модели PLSR и приступает к обучению модели для получения модели измерения объема кроны. Рисунок 12a иллюстрирует сравнение между прогнозируемыми и фактическими значениями тестового набора для модели измерения объема кроны, в то время как Рисунок 12b представляет график рассеяния и график остатков, соответствующий тестовому набору. Графики ясно показывают, что модель измерения объема кроны, обученная с использованием модели PLSR с тремя главными компонентами, достигает низкой ошибки прогноза и демонстрирует сильную способность к обобщению для набора данных, проанализированного в этом исследовании.
Рисунок 12. Результаты тестового набора для модели измерения объема кроны на основе PLSR. (a) График прогнозируемых значений в сравнении с истинными значениями для тестового набора. (b) График точек рассеяния тестового набора в сравнении с аппроксимацией остатков.
3.2. Результаты построения модели измерения объема кроны на основе нейронной сети BP
Результаты перекрестной проверки для 81 комбинации параметров модели нейронной сети BP ранжированы от лучших к худшим в соответствии со средним R2. Худшая комбинация гиперпараметров дает средний R2 всего 0,5833, что почти на 0,4 ниже, чем R2 оптимальной комбинации, составляющий 0,9532, подчеркивая важность выбора лучших гиперпараметров для модели нейронной сети BP. Идентифицированы три лучшие комбинации гиперпараметров, которые продемонстрировали превосходную производительность во время перекрестной проверки для дальнейшего анализа. Конкретные значения выбранных гиперпараметров подробно описаны ниже: комбинация 1 включает (128, 128) скрытых слоев и нейронов в каждом слое, со скоростью обучения 0,01 и коэффициентом регуляризации 0,0001; комбинация 2 состоит из (128, 64) для количества скрытых слоев и нейронов в каждом слое, со скоростью обучения 0,01 и коэффициентом регуляризации 0,00001; комбинация 3 включает (128, 64) для количества скрытых слоев и нейронов в каждом слое, со скоростью обучения 0,01 и коэффициентом регуляризации 0,001. Таблица 2 представляет средние значения R2, RMSE и MAE, полученные с помощью 10-кратной перекрестной проверки для первых трех наборов комбинаций гиперпараметров модели регрессии нейронной сети BP.
Таблица 2. Таблица оценок перекрестной проверки для моделей регрессии нейронной сети BP.
Для комбинации гиперпараметров 1 результаты тестового набора для модели нейронной сети BP дают R2 0,9699, RMSE 0,2032 и MAE 0,1261. В комбинации 2 модель достигает R2 0,9703, RMSE 0,2016 и MAE 0,1317. Наконец, для комбинации 3 результаты тестового набора модели показывают R2 0,9720, RMSE 0,1959 и MAE 0,1190.
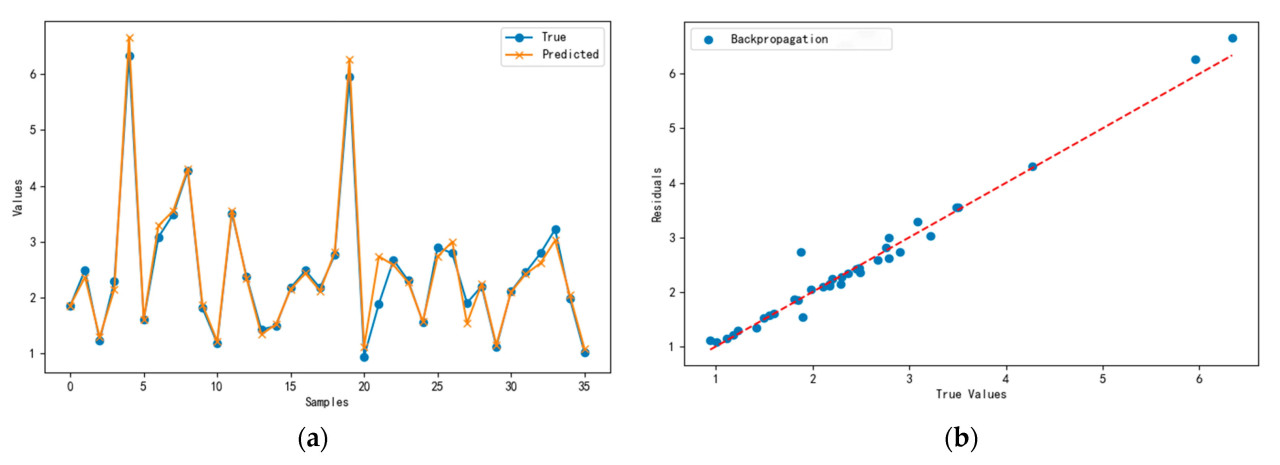
Сравнительный анализ результатов обучения модели нейронной сети BP при различных комбинациях параметров показал, что модель, обученная с комбинацией гиперпараметров 3, достигла наилучшей производительности для оценки объема кроны. Рисунок 13a представляет сравнение между прогнозируемыми и фактическими значениями для тестового набора модели оценки объема кроны, в то время как Рисунок 13b иллюстрирует график рассеяния прогнозов тестового набора вместе с аппроксимацией остатков. Используя комбинацию гиперпараметров 3, алгоритм нейронной сети BP сгенерировал модель оценки объема кроны с минимальной ошибкой между прогнозируемыми и фактическими значениями, демонстрируя сильную способность к обобщению.
Рисунок 13. Результаты тестового набора модели измерения объема кроны на основе нейронной сети BP. (a) График прогнозируемых значений в сравнении с истинными значениями для тестового набора. (b) График точек рассеяния тестового набора в сравнении с аппроксимацией остатков.
3.3. Результаты построения модели измерения объема кроны на основе градиентного бустинга деревьев решений
Среднее R2 комбинации параметров с наихудшей производительностью перекрестной проверки для модели GBDT составляет всего 0,7682, что приблизительно на 0,2 ниже, чем среднее R2 оптимальной комбинации параметров, равное 0,9394. Этот результат подчеркивает значимость оптимизации гиперпараметров для модели GBDT. Три лучшие комбинации гиперпараметров, которые продемонстрировали превосходную производительность во время перекрестной проверки, были идентифицированы для дальнейшего анализа. Конкретные значения выбранных гиперпараметров следующие: комбинация 1 включает 100 деревьев решений, скорость обучения 0,1 и максимальную глубину 3; комбинация 2 состоит из 150 деревьев решений, скорости обучения 0,1 и максимальной глубины 3; и комбинация 3 включает 250 деревьев решений, скорость обучения 0,1 и максимальную глубину 3. Результаты перекрестной проверки для этих трех наборов комбинаций гиперпараметров представлены в Таблице 3.
Таблица 3. Таблица оценок перекрестной проверки модели GBDT.
Когда применяется комбинация гиперпараметров 1, модель GBDT дает R2 тестового набора 0,9315, с RMSE 0,3062 и MAE 0,1732. В случае комбинации гиперпараметров 2 модель дает немного улучшенные результаты, с R2 0,9319, RMSE 0,3055 и MAE 0,1716. Наконец, когда используется комбинация гиперпараметров 3, модель градиентного бустинга деревьев решений достигает R2 0,9319, RMSE 0,3054 и MAE 0,1704.
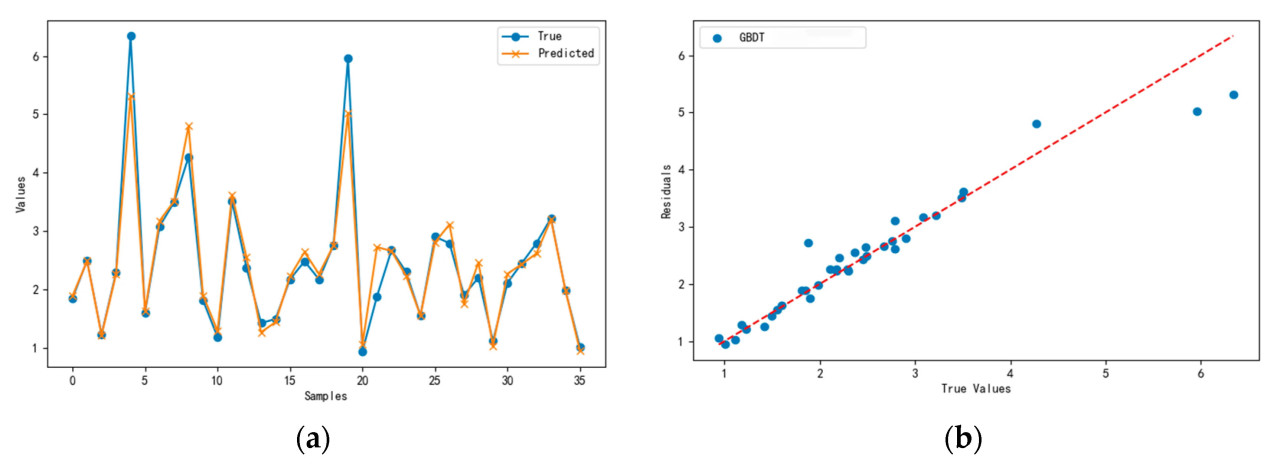
Сравнительный анализ результатов обучения модели GBDT при различных комбинациях параметров показывает, что модель измерения объема кроны, обученная с комбинацией гиперпараметров 3, демонстрирует наивысшую эффективность. Рисунок 14a иллюстрирует сравнение между прогнозируемыми значениями и фактическими значениями для тестового набора модели измерения объема кроны, в то время как Рисунок 14b представляет график рассеяния и график остатков для того же тестового набора. Ошибка между прогнозируемыми и фактическими значениями модели измерения объема кроны, полученной с помощью обучения алгоритма GBDT с комбинацией гиперпараметров 3, минимальна, что указывает на сильную способность к обобщению.
Рисунок 14. Результаты тестового набора модели измерения объема кроны на основе GBDT. (a) График прогнозируемых значений в сравнении с истинными значениями для тестового набора. (b) График точек рассеяния тестового набора в сравнении с аппроксимацией остатков.
3.4. Обзор моделей измерения объема кроны и сравнительный анализ эффектов
В этом наборе данных оптимальные гиперпараметры для модели PLSR включают установку количества главных компонент на 3. Коэффициент детерминации R2 обученной модели измерения объема кроны составляет 0,9742, со среднеквадратичной ошибкой (RMSE) 0,1879 и средней абсолютной ошибкой (MAE) 0,1161. Для модели нейронной сети BP оптимальные гиперпараметры включают количество скрытых слоев и нейронов в каждом слое, соответственно (128, 64), наряду со скоростью обучения 0,01 и коэффициентом регуляризации 0,001. Коэффициент детерминации R2 для обученной модели измерения объема кроны составляет 0,9720, с RMSE 0,1959 и MAE 0,1190. Оптимальные гиперпараметры для модели GBDT состоят из 250 деревьев решений, скорости обучения 0,1 и максимальной глубины дерева 3. Коэффициент детерминации R2 обученной модели измерения объема кроны составляет 0,9319, с RMSE 0,3054 и MAE 0,1704.
Сравнительный анализ показал, что точность аппроксимации модели PLSR была выше, чем у обеих моделей — нейронной сети BP и GBDT. Коэффициенты детерминации модели измерения объема кроны, полученной из модели PLSR, улучшились на 0,0022 по сравнению с моделью нейронной сети BP и на 0,0423 по сравнению с моделью GBDT. Дополнительно, среднеквадратичные ошибки (RMSE) уменьшились на 0,0080 и 0,1175 соответственно, в то время как средние абсолютные ошибки (MAE) снизились на 0,0029 и 0,0543 соответственно. Эти результаты указывают, что модель измерения объема кроны, полученная из модели PLSR, превзошла две другие модели с точки зрения способности к обобщению, смещения прогноза и средней ошибки прогноза.
4. Обсуждение
Данное исследование устанавливает модель оценки объема кроны на основе данных облака точек лидара, которая может эффективно и точно прогнозировать объем кроны, предоставляя значительное руководство для регулирования ветра и контроля дозировки при прецизионном опрыскивании в садах. По сравнению с традиционными ручными измерениями объема кроны, метод, представленный в этом исследовании, снижает субъективные человеческие факторы путем анализа признаков облака точек для получения объема кроны, что приводит к более высокой и стабильной точности модели [7]. В отличие от обычных методов срезов, которые предполагают, что кроны являются сплошными, подход, принятый в этом исследовании, учитывает наличие зазоров в кроне, тем самым снижая погрешности измерения. Улучшенный алгоритм извлечения контура облака точек Alpha Shape, представленный в разделе извлечения признаков, значительно повышает точность оценки профиля кроны. Помимо своей направленности на опрыскивание плодовых деревьев, это исследование также имеет важное значение для исследований в области прогнозирования урожайности плодов и мониторинга лесов.
В практических применениях в садах объем кроны, измеренный в этом исследовании с учетом зазоров, может эффективно отражать как плотность растений, так и плотность материала внутри кроны, включая листья и ветви. Во время опрыскивания присутствие листьев и ветвей может привести к потерям от ветра и адгезии капель. Следующим шагом может быть исследование механизмов потерь от ветра и адгезии капель внутри кроны на основе объема кроны, полученного в этом исследовании, наряду с такими факторами, как плотность листьев и схемы посадки. Это исследование может привести к разработке точных карт дифференцированного опрыскивания для плодовых деревьев. Используя эти карты и связанные стратегии для контроля силы ветра и дозировки во время опрыскивания, можно было бы достичь прецизионного дифференцированного опрыскивания в садах, решая проблему чрезмерного применения, связанную с традиционными методами опрыскивания, одновременно снижая остатки пестицидов, потери и загрязнение окружающей среды, вызванные передозировкой.
Это исследование в основном фокусируется на улучшении методов получения профилей и объемов кроны, а также на оптимизации гиперпараметров и обучении модели оценки объема кроны на основе набора данных, используемого в этом исследовании. Однако оно не учитывает другие факторы, такие как автоматическая обрезка облаков точек. Дополнительно, вариации видов культур, условий роста, стадий роста и методов посадки влияют на разреженность и плотность кроны, что приводит к разным взаимосвязям между объемом кроны и определенными признаками (такими как длина контура кроны). Это свидетельствует, что модели взаимосвязей могут различаться. Для конкретных видов растений оценка объема может использовать улучшенные методы извлечения признаков, предложенные в этом исследовании, для переобучения модели. Влияние различных видов растений и плотности кроны на точность улучшенного алгоритма извлечения контура облака точек Alpha Shape и улучшенного алгоритма объема кроны, представленных в этом исследовании, относительно невелико. Например, Рисунок 15 иллюстрирует сравнение извлечения контура кроны платана и оценки объема. Дальнейшие исследования необходимы для подтверждения конкретных эффектов улучшенных алгоритмов, предложенных в этом исследовании, на разные виды растений.
Рисунок 15. Сравнение извлечения контура кроны платана и получения объема. (a) Сравнение контуров в направлении проекции X. (b) Сравнение контуров в направлении проекции Y. (c) Сравнение контуров в направлении проекции Z. (d) Сравнение получения объема.
5. Выводы
1. Общий алгоритм извлечения контура Alpha Shape страдает от значительных погрешностей из-за ограничений в оценке эффективной границы. Для решения этой проблемы данная статья предлагает улучшенный алгоритм извлечения контура Alpha Shape, который улучшает оценку валидности сегментов контурных линий, тем самым значительно повышая точность результатов извлечения контура.
2. В данном исследовании используется метод интегрирования по сетке для измерения объема кроны. Однако обычные методы интегрирования по сетке часто игнорируют зазоры в кроне при расчете разностей высот, что приводит к значительным погрешностям. Чтобы решить эту проблему, вводится улучшенный метод интегрирования по сетке, который учитывает влияние зазоров при расчетах высоты, тем самым существенно повышая точность измерений объема кроны.
3. В данном исследовании используется метод рекурсивного исключения признаков с перекрестной проверкой на основе случайного леса для отбора признаков из общего числа 10. В конечном итоге, пять признаков были сохранены для набора данных обучения модели: количество облаков точек, 2D-контур облака точек в направлении проекции X, 2D-контур облака точек в направлении проекции Z, 2D-ширина в направлении проекции Y и 2D-длина в направлении проекции Z. Путем исключения нерелевантных или избыточных признаков этот подход повышает точность и прогностическую способность модели измерения объема кроны.
4. Выбор оптимальных гиперпараметров для PLSR, нейронных сетей BP и GBDT был проведен с использованием набора данных из этого исследования, в результате чего были построены модели измерения объема кроны для каждого метода при их соответствующих оптимальных гиперпараметрах. Анализ результатов показал, что модель PLSR с тремя главными компонентами дала наилучшую производительность для измерения объема кроны. Эта модель достигла значения R2 0,9742, с наименьшими RMSE и MAE, равными 0,1879 и 0,1161 соответственно. Эти результаты указывают, что модель обладает сильной способностью к обобщению, низким смещением прогноза и минимальной средней ошибкой прогноза, облегчая быстрое и точное измерение объема кроны плодового дерева.
Ссылки
1. Xu, T.; Lu, X.L.; Qi, Y.N.; Zeng, J.; Lui, X.H.; Yuan, Q.C. Research status on equipment and technology of orchard air-assisted sprayer in China. J. Chin. Agric. Mech. 2023, 44, 69–77. [Google Scholar]
2. Niu, C.Q.; Zhang, W.J.; Wang, Q.; Zhao, X.X.; Fan, G.J.; Jiang, H.H. Current status and trends of research on adjusting air volume of orchard air spray. J. Chin. Agric. Mech. 2020, 41, 48–54. [Google Scholar]
3. He, X. Research progress and developmental recommendations on precision spraying technology and equipment in China. Smart Agric. 2020, 2, 133–146. [Google Scholar]
4. Gu, C.C.; Zhai, C.Y.; Chen, L.P.; Li, Q.; Hu, L.N.; Yang, Z.F. Detection Model of Tree Canopy Leaf Area Based on LiDAR Technology. Trans. Chin. Soc. Agric. Mach. 2021, 52, 278–286. [Google Scholar]
5. Zhao, C.Y.; Zhao, C.J.; Ning, W.; Long, J.; Wang, X.; Weckler, P.; Zhang, H.H. Research progress on precision control methods of air-assisted spraying in orchards. Trans. Chin. Soc. Agric. Eng. 2018, 34, 1–15. [Google Scholar]
6. He, X.Q. Plant protection precision application technology and equipment. Agric. Eng. Technol. 2017, 37, 22–26. [Google Scholar]
7. Ding, W.M.; Zhao, S.Q.; Zhao, S.Q.; Gu, J.B.; Qiu, W.; Guo, B.B. Measurement Methods of Fruit Tree Canopy Volume Based on Machine Vision. Trans. Chin. Soc. Agric. Mach. 2016, 47, 1–10+20. [Google Scholar]
8. Wang, Q.; Hu, H.; Wu, Y.L.; Kang, R.H.; Xu, B.X.; Liang, Z.Y. Automatic Tree Crown Volume Calculation Method Based on Point Cloud Data. J. Chin. J. Northwest For. Univ. 2017, 32, 242–246. [Google Scholar]
9. He, C.; Zhang, S.Y.; Matteo, C.; Zhou, A.M.; Hong, F.X. Algorithm of Crown Volume with Square Grid-based Method. Trans. Chin. Soc. Agric. Mach. 2014, 45, 90–97. [Google Scholar]
10. Yu, D.H.; Feng, Z.K. Tree crown volume measurement method based on oblique aerial images of UAV. Trans. Chin. Soc. Agric. Eng. 2019, 35, 90–97. [Google Scholar]
11. Shu, Y.P.; Li, Q.J.; Zhou, H.P.; Tao, R.; Xu, L.Y. Design of variable rate spray control system based on LiDAR detection. J. For. Eng. 2020, 5, 139–147. [Google Scholar]
12. Ma, W.F.; Wu, X.D.; Wang, C.; Wen, P.; Wang, J.L.; Cao, L.; Xiao, Z.L. A spherical coordinate integration method for extracting crownvolumes of individual trees based on the TLS point clouds. Remote Sens. Nat. Resour. 2024, 36, 81–87. [Google Scholar]
13. Wang, Y.T.; Wang, J.; Niu, L.W.; Cheng, S.P.; Sun, L. Comparative analysis of extraction algorithms for crown volume and surface area using UAV tilt photogrammetry. J. For. Eng. 2022, 7, 166–173. [Google Scholar]
14. Cheng, G.; Wang, J.G.; Yang, J.; Zhao, Z.Z.; Wang, L. Calculation Method of 3D Point Cloud Canopy Volume Based on Improved α-shape Algorithm. Trans. Chin. Soc. Agric. Mach. 2021, 52, 175–183. [Google Scholar]
15. Yu, L.; Huang, J.; Zhao, Z.X.; Zhang, L.; Sun, D.Z. Laser Measurement and Experiment of Hilly Fruit Tree Canopy Volume. Trans. Chin. Soc. Agric. Mach. 2013, 44, 224–228. [Google Scholar]
16. Li, Q.J.; Zheng, J.Q.; Zhou, H.P.; Zhang, H.; Shu, P.Y.; Xu, B. Online Measurement of Tree Canopy Volume Using Vehicle-borne 2-D Laser Scanning. Trans. Chin. Soc. Agric. Mach. 2016, 47, 309–314. [Google Scholar]
17. Li, P.; Zhang, M.; Dai, X.S.; Wang, T.; Zheng, J.Q.; Yi, L.S.; Lyu, Q. Real-Time Estimation of Citrus Canopy Volume Based on Laser Scanner and Irregular Triangular Prism Module Method. Sci. Agric. Sin. 2019, 52, 4493–4504. [Google Scholar]
18. Zhou, H.; Zhang, J.; Ge, L.; Yu, X.; Wang, Y.; Zhang, C. Research on volume prediction of single tree canopy based on three-dimensional (3D) LiDAR and clustering segmentation. Int. J. Remote Sens. 2021, 42, 738–755. [Google Scholar] [CrossRef]
19. Underwood, J.P.; Hung, C.; Whelan, B.; Sukkarieh, S. Mapping almond orchard canopy volume, flowers, fruit and yield using lidar and vision sensors. Comput. Electron. Agric. 2016, 130, 83–96. [Google Scholar] [CrossRef]
20. Xu, L.; Hou, J.; Cheng, Q.L.; Qing, Y.Q.; Peng, Y.C.; Huang, G. A new adaptive median denoising model combined with cyclic iterative method. J. Sichuan Univ. (Nat. Sci. Ed.) 2022, 59, 51–60. [Google Scholar]
21. Lei, K.; Tang, X.; Li, X.; Lu, Q.; Long, T.; Zhang, X.; Xiong, B. Research and Preliminary Evaluation of Key Technologies for 3D Reconstruction of Pig Bodies Based on 3D Point Clouds. Agriculture 2024, 14, 793. [Google Scholar] [CrossRef]
22. Zhang, L.; Hao, Q.; Mao, Y.; Su, J.; Cao, J. Beyond Trade-Off: An Optimized Binocular Stereo Vision Based Depth Estimation Algorithm for Designing Harvesting Robot in Orchards. Agriculture 2023, 13, 1117. [Google Scholar] [CrossRef]
23. Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
24. Edelsbrunner, H.; Kirkpatrick, D.; Seidel, R. On the shape of a set of points in the plane. IEEE Trans. Inf. Theory 1983, 29, 551–559. [Google Scholar] [CrossRef]
25. Alpha Shapes Extract 2D Point Cloud Boundaries. Available online: https://blog.csdn.net/a394467238/article/details/132556295 (accessed on 7 December 2023).
26. Calculation of Point Cloud Volume Based on Python Grid Method. Available online: https://blog.csdn.net/m0_56729804/article/details/135017822 (accessed on 2 April 2024).
27. Wei, X.H.; Wang, Y.G.; Zheng, J.; Wang, M.; Feng, Z.K. Tree Crown Volume Calculation Based on 3-D Laser Scanning Point Clouds Data. Trans. Chin. Soc. Agric. Mach. 2013, 44, 235–240. [Google Scholar]
28. Shen, Y.; Li, Q.Z.; Du, X.; Wang, H.Y.; Zhang, Y. Indicative features for identifying corn and soybean using remote sensing imagery at middle and later growth season. Natl. Remote Sens. Bull. 2022, 26, 1410–1422. [Google Scholar] [CrossRef]
29. Dash, M.; Liu, H. Feature selection for classification. Intell. Data Anal. 1997, 1, 131–156. [Google Scholar] [CrossRef]
30. Sun, D.L.; Chen, D.L.; Mi, C.L.; Chen, X.Y.; Mi, S.W.; Li, X.Q. Evaluation of landslide susceptibility in the gentle hill-valleyareas based on the interpretable random forest-recursivefeature elimination model. J. Geomech. 2023, 29, 202–219. [Google Scholar]
31. Zhang, L.; Guo, Z.G.; Qi, S.; Wu, B.C.; Li, P. Predicting shallow landslides in highly vegetation-covered areas using machine learning models. Trans. Chin. Soc. Agric. Eng. 2024, 40, 149–160. [Google Scholar]
32. Zhang, G.Q.; Gan, Z.L.; Yan, Y.; Gao, W.M. Rapid detection of the physicochemical properties of honey based on infrared spectroscopy. Trans. Chin. Soc. Agric. Eng. 2023, 39, 275–284. [Google Scholar]
33. Zhao, J.; Shen, M.S.; Pu, Y.G.; Chen, A.; Li, H. Out-of-warehouse Evaluation and Prediction Model of AppleBased on Near-infrared Spectroscopy Combined with Multiple Quality Indexes. Trans. Chin. Soc. Agric. Mach. 2023, 54, 386–395. [Google Scholar]
34. Chen, W.J.; Zhou, D.Q.; Cui, C.H.; Ren, Z.J.; Zuo, W.J. Prediction Model of Farinograph Characteristics of Wheat Flour Based on Near Infrared Spectroscopy. Spectrosc. Spectr. Anal. 2023, 43, 3089–3097. [Google Scholar]
35. An, X.F.; Dai, J.Y.; Li, L.W.; Lu, H.; Yin, Y.X.; Meng, Z.J. Research on wheat moisture content prediction model for combine harvester based on GA-BP method. Trans. Chin. Soc. Agric. Mach. 2024, 1–10. Available online: http://kns.cnki.net/kcms/detail/11.1964.S.20241016.1603.004.html (accessed on 12 December 2024).
36. He, B.; Li, L.Q.; Chengjiang, Y.C.; Zhou, Z.X.; Zhang, L.; Liang, X.C. Performance prediction of PV/T cogeneration system based on artificial neural network. Trans. Chin. Soc. Agric. Eng. 2024, 40, 309–318. [Google Scholar]
37. Liu, T.C.; Dong, K.Y.; Zhang, B.; Song, Y.S.; Liang, Z.L.; Li, J.W.; Wang, Y.B.; Zhang, L.; Yan, G.Q.; Hu, W.Y. A Grid-Based BP Neural Network Positioning Method for a Space Optical Communication Spot Center. Chin. J. Lasers 2024, 51, 206–213. [Google Scholar]
38. Li, H.X.; Song, D.L.; Kong, J.N.; Song, Y.F.; Chang, H.Y. Evaluation of Hyperparameter Optimization Techniques for Traditional Machine Learning Models. Comput. Sci. 2024, 51, 242–255. [Google Scholar]
39. Meng, R.; Shen, W.; Luan, Q.F.; Ji, Q.; Rao, Y.L. Water depth retrieval based on gradient boosting decision tree algorithm. Trans. Oceanol. Limnol. 2023, 45, 45–50. [Google Scholar]
40. Zeng, P.Z.; Wang, W.; Yuan, M.X.; Yang, Z.F. Research on Inversion of Nitrogen Content in Apple Tree Canopy Based on Remote Sensing of Unmanned Aerial Vehicles. Shandong Agric. Sci. 2024, 56, 167–173. [Google Scholar]
Guo N, Xu N, Kang J, Zhang G, Meng Q, Niu M, Wu W, Zhang X. A Study on Canopy Volume Measurement Model for Fruit Tree Application Based on LiDAR Point Cloud. Agriculture. 2025; 15(2):130. https://doi.org/10.3390/agriculture15020130
Перевод статьи «A Study on Canopy Volume Measurement Model for Fruit Tree Application Based on LiDAR Point Cloud» авторов Guo N, Xu N, Kang J, Zhang G, Meng Q, Niu M, Wu W, Zhang X., оригинал доступен по ссылке. Лицензия: CC BY. Изменения: переведено на русский язык


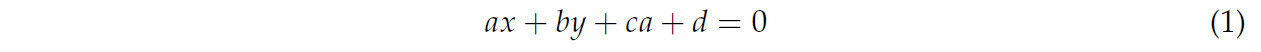
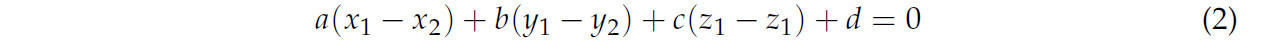
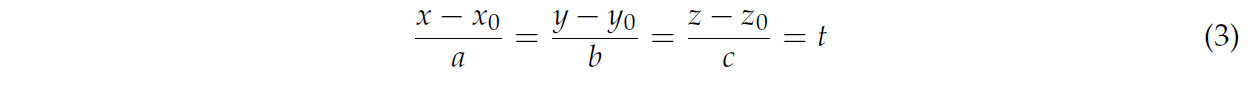
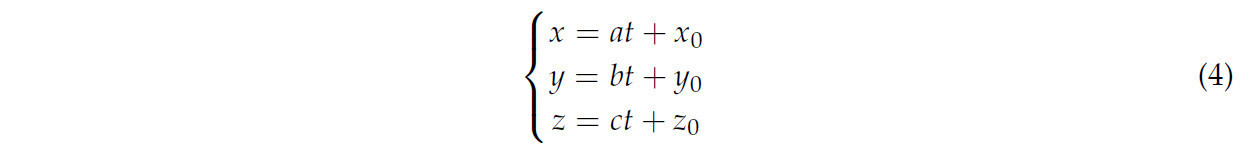
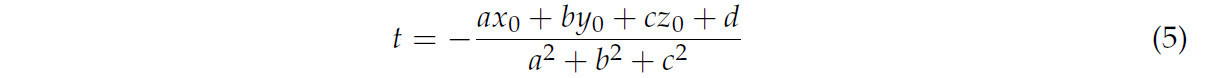
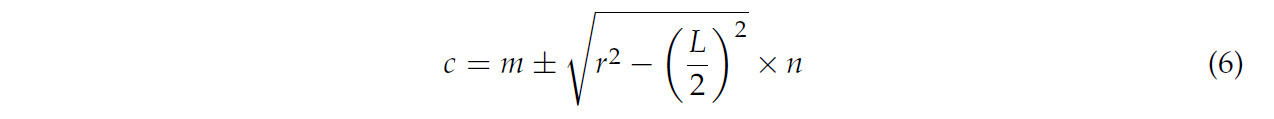
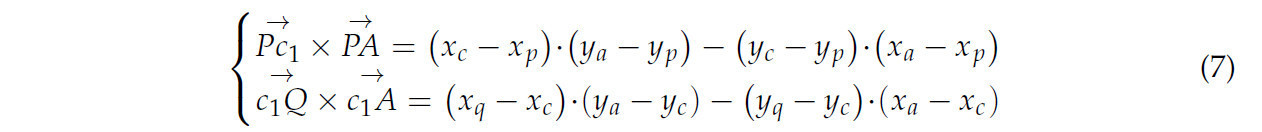

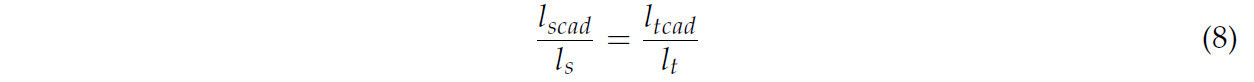


































































































Комментарии (0)