Метод калибровки параметров дискретно-элементного моделирования почво-растительных остатков пшеницы на засоленных прибрежных почвах
После уборки пшеницы на засоленных прибрежных почвах при заделке соломы и фрезерной обработке почвы отсутствие надежных моделей параметров для дискретно-элементного моделирования в определенной степени сдерживает оптимизацию и усовершенствование специальных машин для обработки и подготовки почвы на засоленных землях. В данном исследовании для калибровки параметров дискретно-элементного моделирования использовалась модель Герца–Миндлина с JKR-адгезией.
Аннотация
Принимая угол естественного откоса смеси почвы и растительных остатков пшеницы в качестве тестового показателя, с помощью теста Плэкетта–Бермана и теста наискорейшего подъема были отобраны четыре группы параметров, существенно влияющих на угол откоса, и определены диапазоны их оптимальных значений. Затем был проведен эксперимент по методу Бокса–Бенкена для получения квадратичной регрессионной модели, связывающей значимые параметры с углом откоса, и определения их оптимальных значений. Оптимальная комбинация параметров была использована в имитационных испытаниях. Относительные погрешности между измеренными значениями и результатами имитационных испытаний для угла естественного откоса и степени покрытия почвы остатками пшеницы составили 0,74% и 1,34% соответственно. Полученные достоверные параметры обеспечивают теоретическую основу для оптимизации и усовершенствования оборудования для подготовки почвы на засоленных землях.
1. Введение
В качестве важного недостаточно используемого земельного ресурса в нашей стране, засоленные прибрежные почвы имеют большой потенциал развития и экономическую ценность. Рациональное освоение и использование этих земель являются ключевыми стратегиями для решения дефицита земельных ресурсов и обеспечения продовольственной безопасности. Заделка соломы в поле может эффективно улучшить структуру почвы, снизить ее объемную плотность, улучшить водопроницаемость, значительно сохранить влагу в почве, подавить накопление солей на поверхности, способствовать росту и развитию сельскохозяйственных культур и повысить урожайность [1]. Однако в процессе заделки соломы и фрезерной обработки почвы возникают такие проблемы, как высокое сопротивление при работе и намотка пожнивных остатков пшеницы на рабочие органы. Поэтому изучение законов взаимодействия между почвой и пожнивными остатками пшеницы с использованием метода дискретно-элементного моделирования имеет большое значение для защиты почв засоленных земель и практики заделки соломы.
В последние годы некоторые ученые провели исследования по калибровке параметров моделирования для различных типов почв, растительных остатков и рабочих органов. Например, Ши Жуйцзе и др. [2] рассмотрели недостаток исследований в области дискретных элементов ключевых аспектов, таких как изменение положения и характеристики движения стеблей льна во время уборки. Они построили гибкую модель стеблей льна, используя модель связывания в методе дискретных элементов, предоставляя справочную информацию для дискретно-элементного моделирования стеблей льна. Сун Шаолун и др. [3] взяли почву на хлопковых полях Синьцзяна после вспашки в качестве объекта исследования и провели калибровку параметров моделирования с помощью метода комбинированного тестирования с общим ротационным центром, предоставляя теоретическую основу и техническую поддержку для исследований по снижению сопротивления устройств для послойного внесения удобрений на хлопковых полях. Чжоу Хуа и др. [4] взяли типичную почву пахотного слоя кукурузных полей в качестве объекта исследования и, на основе контактной модели Герца–Миндлина (без проскальзывания), используя метод планирования центральных композиционных испытаний, откалибровали модель дискретных элементов, которую можно использовать для построения типичной почвы пахотного слоя кукурузных полей, предоставляя теоретическую основу для построения моделей почвы пахотного слоя кукурузных полей. Чжао Чжихао и др. [5] выбрали модель Герца–Миндлина с JKR-адгезией в качестве контактной модели для моделирования почвы, чтобы откалибровать параметры моделирования почвы и рисовой стерни, и провели анализ траектории фрезерной обработки почвы и рисовой стерни на основе MBD-DEM, проверив точность калибровки параметров моделирования, предоставляя надежные контактные параметры для анализа дискретных элементов процесса регулирования траектории обработки рисовой стерни. Ся Цзюньфан и др. [6] взяли рисовую солому в качестве объекта исследования, на основе контактной модели Герца–Миндлина со связующим эффектом, использовали метод замены частиц для построения гибкой модели дискретных элементов рисовой соломы и провели калибровку параметров контактной модели дискретных элементов и верификацию многоусловных испытаний, предоставляя справочную информацию для оптимального проектирования рабочих органов машин для заделки соломы.
Хотя отечественные и зарубежные ученые провели большое количество исследований по калибровке параметров дискретно-элементного моделирования для различных типов почвы и соломы [7,8,9,10,11,12,13], отсутствуют точные модели дискретно-элементного моделирования для проблем высокого сопротивления, трудного крошения почвы и намотки пожнивных остатков при обработке засоленных прибрежных почв. Для решения этих проблем в данном исследовании была выбрана смесь почвы и соломы после уборки пшеницы на засоленных почвах дельты реки Хуанхэ в качестве объекта исследования, а основные физические параметры и контактные параметры были получены экспериментальным путем. Угол естественного откоса смеси почвы и соломы использовался в качестве калибровочного параметра. С помощью теста Плэкетта–Бермана были отобраны факторы, оказывающие значительное влияние на угол откоса. Затем оптимальный диапазон значений значимых факторов был определен с помощью теста наискорейшего подъема. Наконец, с помощью теста Бокса–Бенкена была получена квадратичная регрессионная модель, связывающая значимые параметры с углом откоса. Значимые параметры были оптимизированы с измеренным углом откоса в качестве целевого значения, чтобы получить оптимальную комбинацию параметров дискретно-элементного моделирования для смеси почвы и соломы. Параметры были проверены в полевых экспериментах, а точность модели дискретных элементов была подтверждена путем сравнения и анализа относительных ошибок результатов испытаний. Цель состоит в том, чтобы установить точную модель дискретных элементов смеси почвы и соломы в пахотном слое засоленных прибрежных почв, предоставляя справочную информацию для создания моделей дискретно-элементного моделирования процесса взаимодействия между почвой и соломой и почворазрушающих и противостерневых рабочих органов специальных машин для обработки засоленных земель, оптимизации этих рабочих органов, снижения энергозатрат при работе и повышения адаптируемости и производительности машин для обработки почвы в засоленных условиях.
2. Определение параметров почвы и пожнивных остатков пшеницы
2.1. Отбор проб смеси почвы и пожнивных остатков пшеницы
В данном исследовании в качестве объекта исследования была выбрана смесь почвы и пожнивных остатков пшеницы. Место отбора проб находилось на демонстрационной базе сельскохозяйственных испытаний на засоленных почвах в сельскохозяйственной высокотехнологичной зоне Хуантреугольник, город Дунъин, провинция Шаньдун (географические координаты: 37,297° с.ш., 118,648° в.д.), а значение pH почвы в этом районе составляло 8,3. В соответствии с принципом «случайность, равное количество и несколько точек» в эксперименте использовался метод пятиточечного отбора проб для сбора 0–150 мм смешанных материалов почвы и пожнивных остатков пшеницы из пахотного слоя стерневого поля перед фрезерной обработкой после уборки пшеницы в качестве исследуемых образцов. Затем были определены физические параметры и контактные параметры почвы и пожнивных остатков пшеницы соответственно.
2.2. Эксперимент по определению основных физических параметров почвы и пожнивных остатков пшеницы
2.2.1. Плотность почвы и гранулометрический состав
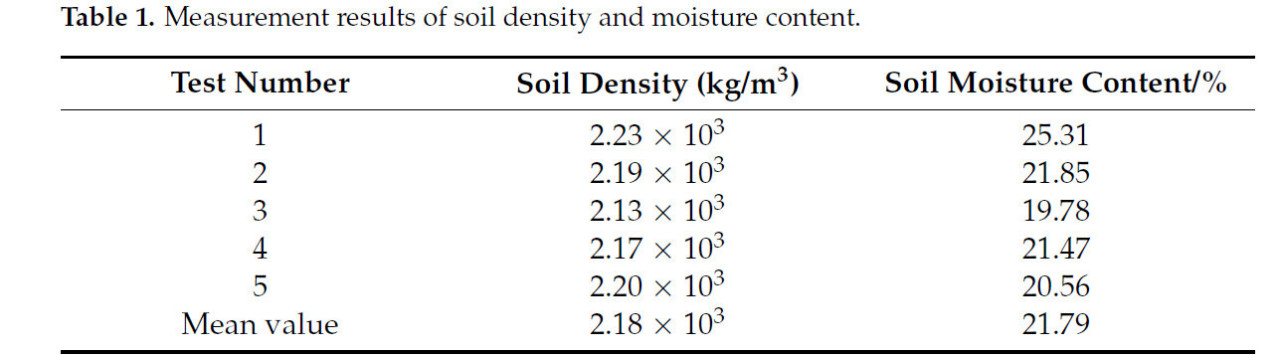
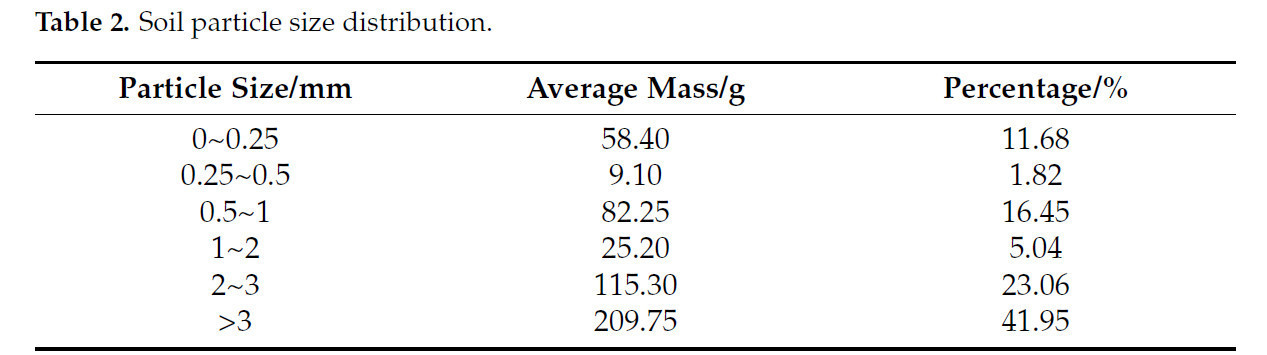
Для определения физических свойств почвы использовался режущий цилиндр объемом 200 см³ для отбора проб почвы с пяти различных участков. Согласно расчетной формуле плотности почвы (1), средняя измеренная плотность почвы составила 2,18 × 10³ кг/м³. С помощью прибора для мониторинга окружающей среды TOP CLOUD-AGRITECHNOLOGYCO и датчика влажности почвы (Рисунок 1a) средняя влажность почвы составила 21,79%. Данные испытаний представлены в Таблице 1. Образец почвы массой 500 г был высушен, и испытание на просеивание почвы было проведено с использованием стандартного лабораторного сита. После обработки образца на равномерно вибрирующем сите в течение 10 мин частицы почвы разного размера на каждом поддоне были точно взвешены. Просеянные частицы показаны на Рисунке 1b, а данные распределения частиц по размерам представлены в Таблице 2.
где ρ — плотность почвы, кг/м³; m — общая масса режущего цилиндра и образца почвы, кг; m1 — масса режущего цилиндра, кг; V — объем режущего цилиндра, см³.
Рисунок 1. Определение влажности почвы и гранулометрического состава. (a) Определение влажности почвы; (b) испытание на просеивание почвы.
Таблица 1. Результаты измерений плотности и влажности почвы.
Таблица 2. Гранулометрический состав почвы.
2.2.2. Испытание почвы на прямой срез
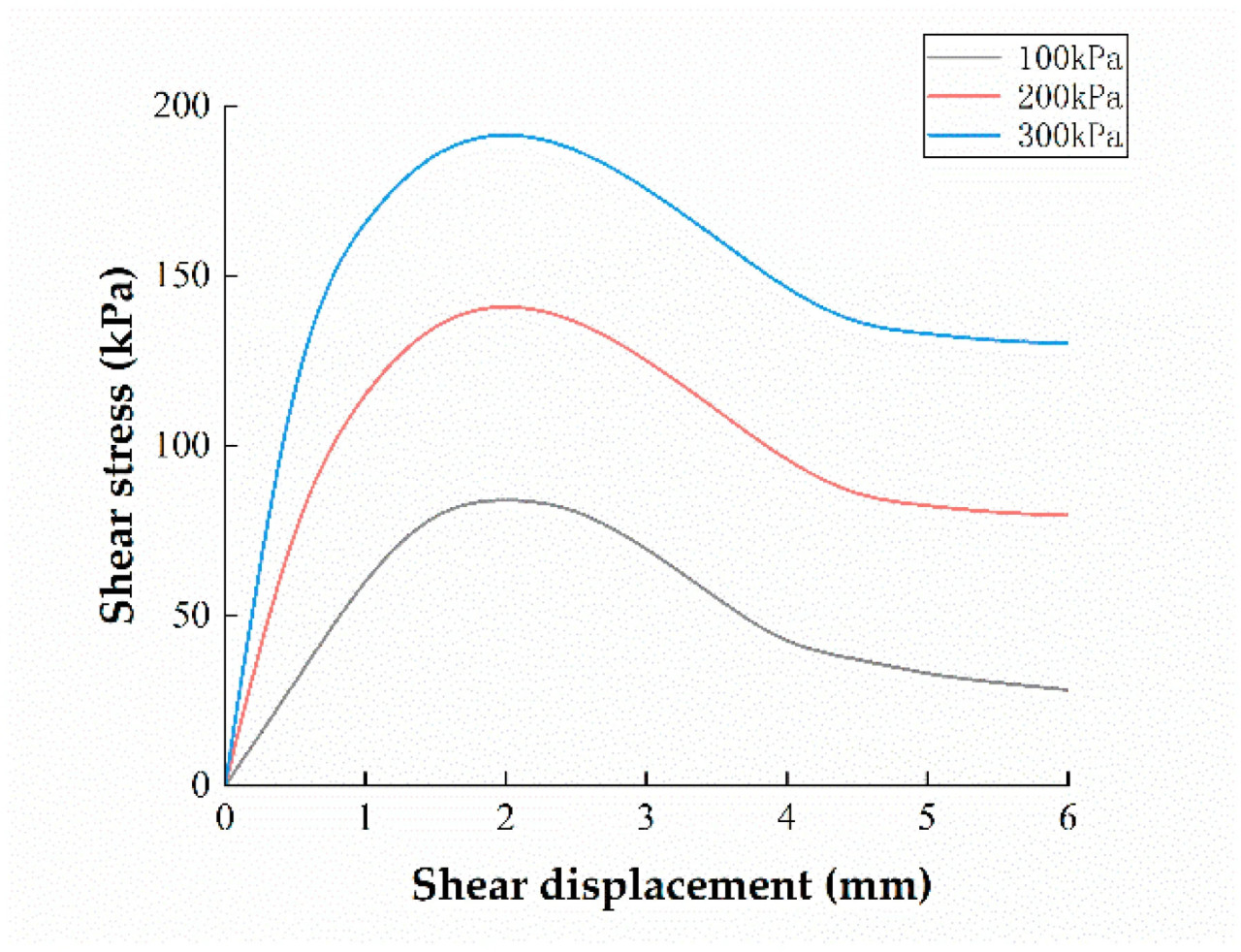
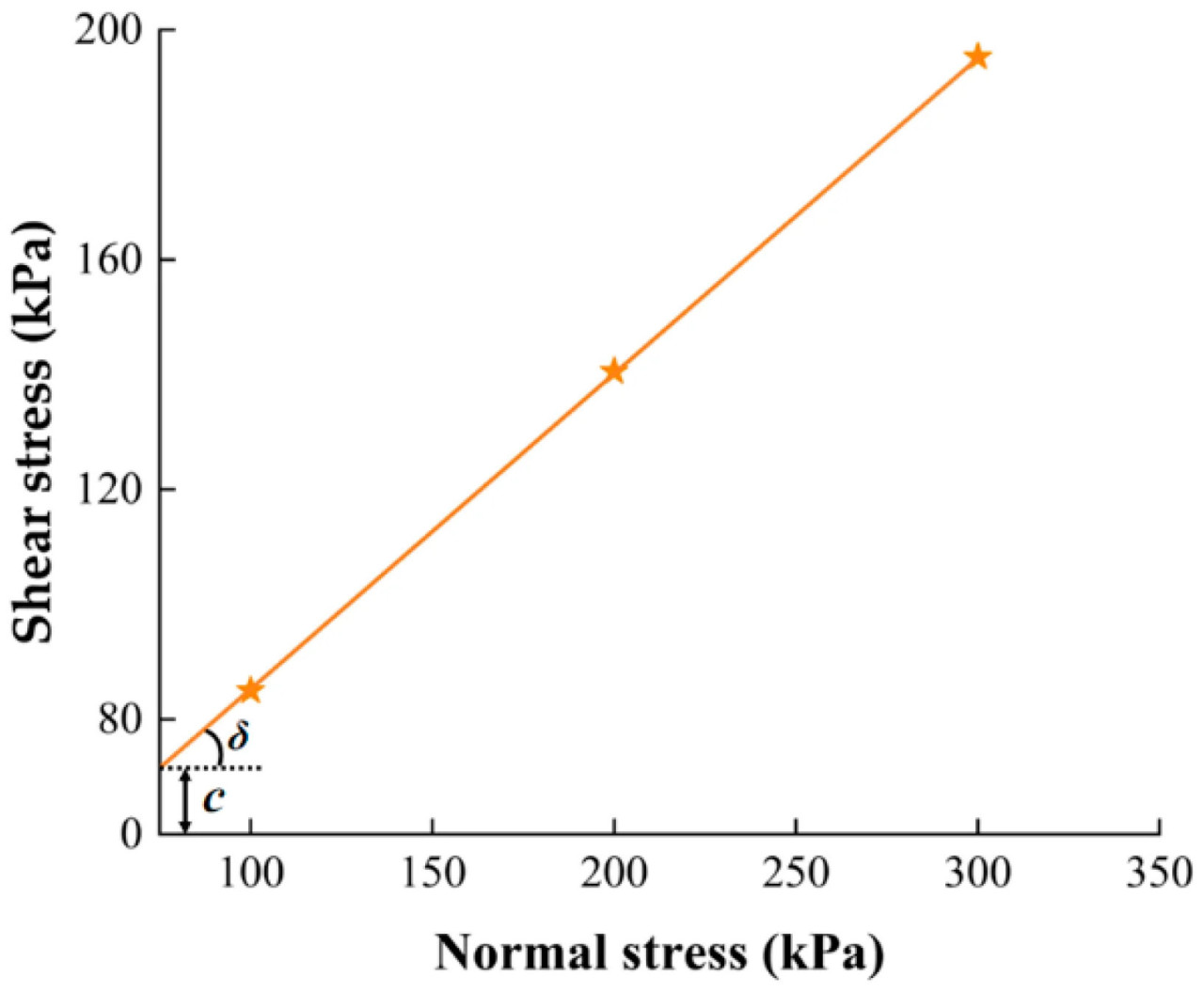
Коэффициент Пуассона — это физическая величина, характеризующая степень изменения поперечного размера относительно продольного, когда материал подвергается осевому растягивающему или сжимающему напряжению. Это имеет большое значение для изучения характеристик деформации материала под действием силы. Для испытания почвы использовался прибор для прямого среза с управлением деформацией ZJ-1B. Измеренный тест на прямой срез почвы показан на Рисунке 2. Для испытания использовались нормальные напряжения 100 кПа, 200 кПа и 300 кПа и скорость сдвига 0,5 мм/мин. Принимая смещение почвы при сдвиге за горизонтальную координату, а напряжение сдвига τ за вертикальную координату, были построены кривые зависимости напряжения сдвига почвы от смещения при сдвиге, как показано на Рисунке 3. Пиковое значение каждой линии на Рисунке 3 выбирается в качестве соответствующей прочности на сдвиг при нормальном напряжении, и строится огибающая прочности по Мору–Кулону [14], как показано на Рисунке 4. Угол между линией и горизонтальной координатой является углом внутреннего трения δ, а пересечение линии с вертикальной координатой является силой сцепления почвы c [15].
Рисунок 2. Испытание почвы на прямой срез. (a) Прибор для прямого среза с управлением деформацией ZJ-1B; (b) образец почвы для испытаний.
Рисунок 3. Кривые зависимости напряжения сдвига почвы от смещения при сдвиге.
Рисунок 4. Диаграмма огибающей прочности по Мору–Кулону.
Напряжение сдвига рассчитывается следующим образом:
где τ — напряжение сдвига, кПа; C0 — калибровочный коэффициент силового кольца, принимается равным 153,25 кПа/мм; R — максимальное показание микрометра силового кольца при сдвиге, мм.
Формула для расчета прочности почвы на сдвиг:
где τf — прочность почвы на сдвиг, кПа; c — сцепление почвы, кПа; δ — угол внутреннего трения почвы (°).
Формула для расчета коэффициента Пуассона почвы следующая:
где K — коэффициент измерения давления почвы; δ — угол внутреннего трения почвы (°); υ — коэффициент Пуассона почвы.
Согласно Рисунку 4 и Уравнению (3), угол внутреннего трения почвы составляет 31,93°, а согласно Уравнениям (4) и (5), коэффициент Пуассона почвы равен 0,32.
На стадии упругой деформации материала модуль сдвига представляет собой отношение напряжения сдвига к соответствующей деформации сдвига. Во время испытания сначала штангенциркулем точно измеряли толщину L образца почвы перед сжатием [16]. Затем образец почвы естественным образом помещали на платформу электронной универсальной испытательной машины, и давление прикладывалось с постоянной скоростью нагружения 0,1 мм/с с помощью круглого индентора. Записывая данные о силе F и деформации ΔL образца почвы, чтобы обеспечить надежность данных, процесс испытания повторяли 5 раз. Согласно формулам (6)–(9), среднее значение модуля упругости составляет 3,168 × 10⁶ кПа, а среднее значение модуля сдвига составляет 1,2 × 10⁶ кПа.
где ε — деформация почвы; ΔL — величина деформации образца почвы после сжатия, мм; L — начальная высота образца почвы, мм; D — диаметр образца почвы, мм; A — площадь контакта между образцом почвы и индентором, мм²; F — осевая нагрузка на образец почвы, Н; E — модуль упругости, кПа; G — модуль сдвига, кПа.
2.2.3. Испытание физических параметров пожнивных остатков пшеницы
Для определения физических свойств пожнивных остатков пшеницы образцы пожнивных остатков пшеницы сначала подвергались удалению почвы, промывке и резке. Затем образцы точно взвешивались с помощью электронных весов, и выбирался мерный цилиндр объемом 1000 мл. После добавления соответствующего количества воды записывался начальный уровень жидкости. После стабилизации уровня жидкости взвешенные образцы пожнивных остатков пшеницы добавляли в мерный цилиндр, и уровень жидкости записывали снова. Эксперимент показан на Рисунке 5. После пятикратного повторения эксперимента, с результатами, подробно описанными в Таблице 3, средняя плотность пожнивных остатков пшеницы была рассчитана с использованием формулы плотности и составила 241 кг/м³. Из-за небольшого размера пожнивных остатков пшеницы было трудно измерить их модуль сдвига и коэффициент Пуассона в эксперименте, поэтому коэффициент Пуассона и модуль сдвига пожнивных остатков пшеницы были взяты из литературы [17,18,19] и составили 0,39 и 5,52 × 10⁶ кПа соответственно.
Рисунок 5. Определение плотности пожнивных остатков пшеницы.
Таблица 3. Результаты измерения плотности пожнивных остатков пшеницы.
2.3. Определение контактных параметров почвы и пожнивных остатков пшеницы
При построении модели смешанного материала почвы и пожнивных остатков пшеницы, помимо учета физических характеристик почвы и пожнивных остатков пшеницы по отдельности, необходимо обращать внимание на контактные параметры их взаимодействия, что является решающим для точности модели [20]. Поэтому коэффициент статического трения, коэффициент качения и коэффициент восстановления при столкновении между почвой и пожнивными остатками пшеницы должны быть точно определены перед работой по дискретно-элементному моделированию и калибровке.
2.3.1. Испытание коэффициента статического трения
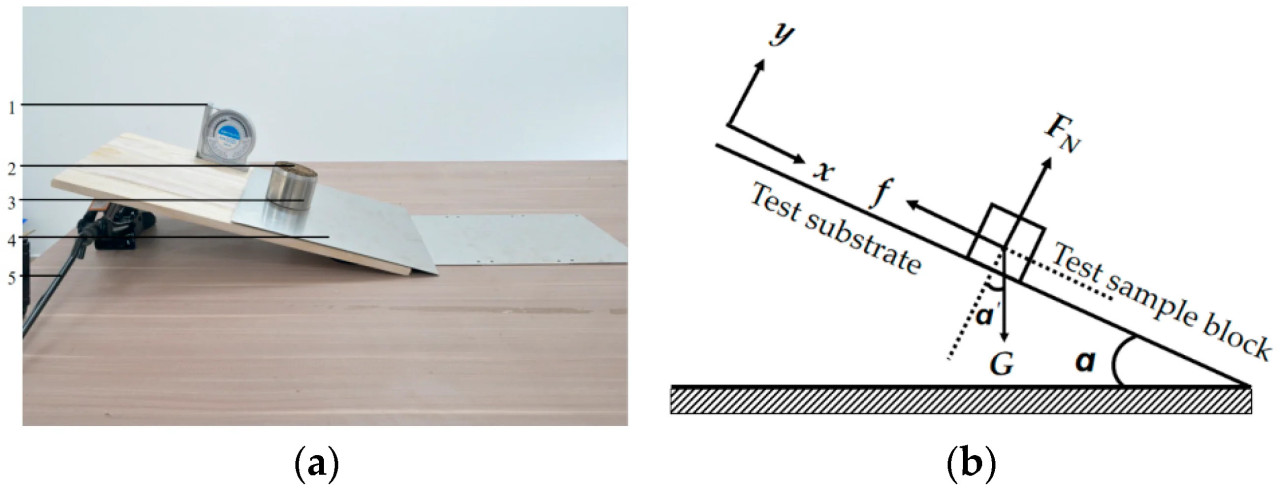
Коэффициент статического трения определяется как отношение максимальной силы статического трения к нормальному давлению между двумя контактирующими объектами. На подготовительном этапе эксперимента почву и пожнивные остатки пшеницы равномерно наносили на подложку отдельно, чтобы подготовить необходимые для столкновения подложку из почвы и пожнивных остатков пшеницы, и были подготовлены тестовые блоки почвы и соломы. Во время процесса измерения тестовые образцы последовательно помещали в контейнеры с двумя открытыми концами, а высокоточный универсальный уровень фиксировали на подложке и калибровали [21]. Мы медленно поднимали контейнер так, чтобы он отделился от контактной пластины, но тестовый образец внутри не вытекал из контейнера. В этот момент мы медленно поворачивали рукоятку управления и увеличивали угол наклона с постоянной скоростью, пока не был записан угол α, когда образец начал скатываться. Чтобы обеспечить надежность данных, каждая экспериментальная группа повторялась пять раз для расчета соответствующего диапазона коэффициентов статического трения между почвой и пожнивными остатками пшеницы, 65Mn стали между собой и друг с другом. Коэффициент качения рассчитывается согласно Уравнению (10), а результаты показаны в Таблице 4. Измерительное устройство и анализ сил показаны на Рисунке 6.
где μ — коэффициент статического трения; f — сила скольжения, Н; FN — сила реакции опоры пластины на материал статического трения, Н; Gp — сила тяжести материала статического трения, Н; a — угол наклона пластины в момент, когда материал статического трения начинает двигаться (°).
Рисунок 6. Испытание для определения коэффициента статического трения почвы. (a) Испытательный стенд для определения коэффициента статического трения; (b) Схематическая диаграмма испытания измерения коэффициента статического трения. 1. Высокоточный универсальный уровень; 2. тестовый образец; 3. контейнер для тестового образца; 4. подложка; 5. регулировочная рукоятка.
Таблица 4. Результаты измерения коэффициента статического трения.
2.3.2. Испытание коэффициента качения (продолжение)
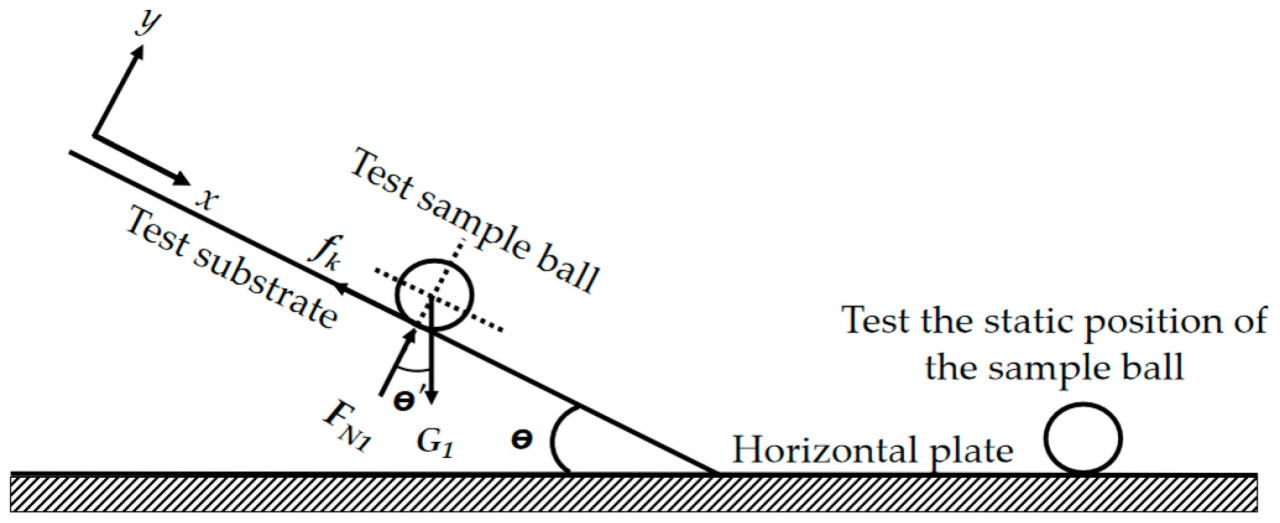
нии объект измерения помещали горизонтально на горизонтальную подложку и медленно поднимали подложку, вращая рукоятку [22]. Когда наблюдалось, что объект измерения катится по подложке без проскальзывания, вращение рукоятки прекращали. В этот момент угол наклона θ подложки точно измеряли с помощью высокоточного универсального уровня. Для обеспечения надежности данных каждая группа экспериментов повторялась 5 раз для расчета соответствующего диапазона коэффициентов трения качения для почвы, пожнивных остатков пшеницы, 65Mn стали между собой и их комбинаций друг с другом. Коэффициент трения качения рассчитывается по формулам (11)–(14), а результаты представлены в Таблице 5. Принцип показан на Рисунке 7.
где M — момент трения качения, Н·м; fk — коэффициент трения качения; FN1 — сила реакции опоры наклонной плоскости на материал трения качения, Н; G1 — сила тяжести материала трения качения, кг; θ — критический угол трения качения материала, (°); r — радиус материала трения качения, мм.
Рисунок 7. Схематическая диаграмма испытания измерения коэффициента трения качения.
Таблица 5. Результаты испытаний коэффициента трения качения.
2.3.3. Испытание измерения коэффициента восстановления при столкновении
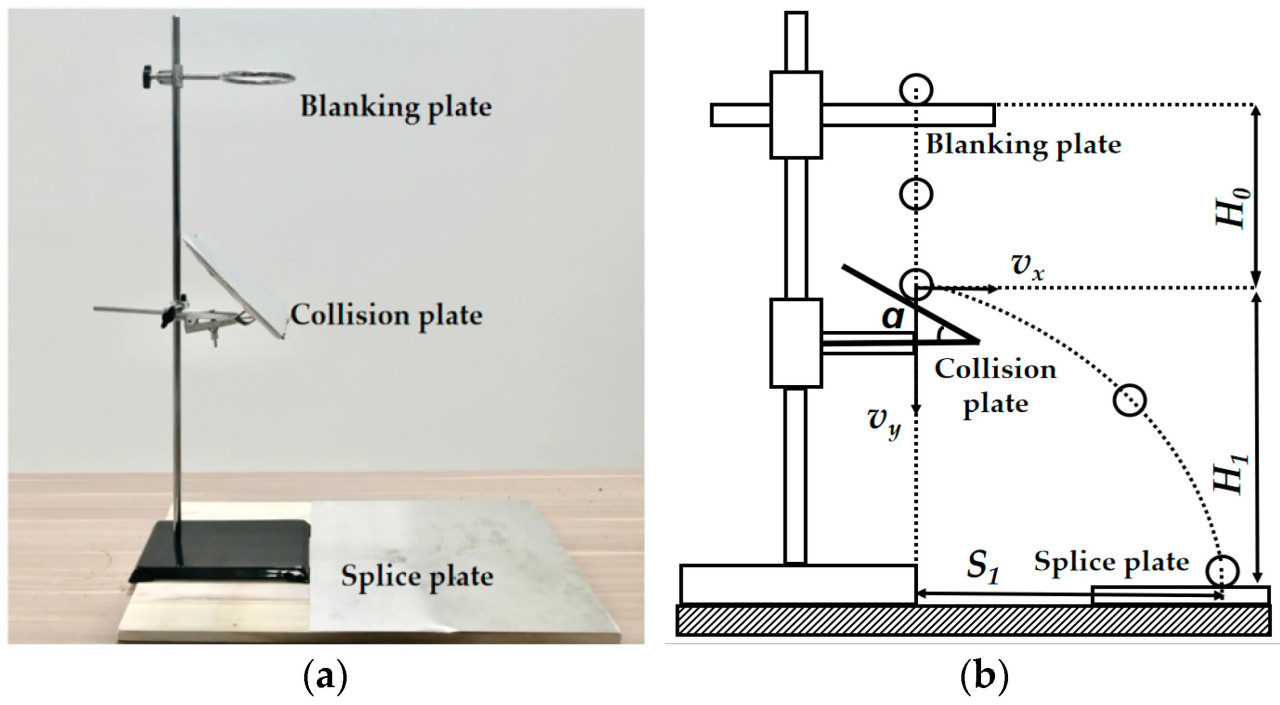
Коэффициент восстановления при столкновении определяется как отношение нормальной скорости центра масс в момент завершения столкновения к нормальной скорости центра масс до столкновения. Этот коэффициент является ключевым параметром для оценки способности объектов восстанавливаться после деформации. Во время эксперимента обрезанные пожнивные остатки пшеницы и заранее подготовленные образцы почвы свободно падали без начальной скорости с высоты 200 мм над пластиной столкновения, а затем сталкивались с различными пластинами столкновения непосредственно под ними [23]. Ударная пластина была изготовлена из почвы, стали 65Mn и пожнивных остатков пшеницы. Испытание образца проводилось при плоскопараллельном движении, и в итоге он приземлялся на приемную пластину, а высота отскока регистрировалась высокоскоростной камерой [24]. Эксперимент повторяли 5 раз и рассчитывали соответствующие коэффициенты восстановления при столкновении для почвы, пожнивных остатков пшеницы, стали 65Mn между собой и их комбинаций друг с другом. Коэффициент восстановления при столкновении рассчитывается по формулам (15)–(21), а результаты представлены в Таблице 6. Измерительное устройство и принцип испытания показаны на Рисунке 8.
где e — коэффициент восстановления при столкновении; Vn — нормальная скорость до столкновения между сталкивающимся материалом и пластиной столкновения, м/с; Vn′ — нормальная скорость после столкновения между сталкивающимся материалом и пластиной столкновения, м/с; V0 — скорость сталкивающегося материала в момент достижения точки столкновения, м/с; H0 — вертикальное расстояние между исходным положением сталкивающегося материала и пластиной столкновения, мм; H1 — вертикальное расстояние между точкой столкновения сталкивающегося материала и приемной пластиной, мм; S1 — горизонтальное расстояние между точкой удара сталкивающегося материала и точкой приземления на приемной пластине, мм.
Рисунок 8. Испытание измерения коэффициента восстановления при столкновении. (a) Испытательный стенд для определения коэффициента восстановления при столкновении; (b) Схематическая диаграмма измерения коэффициента восстановления при столкновении.
Таблица 6. Результаты измерения коэффициента восстановления при столкновении.
3. Калибровка контактных параметров моделирования для смешанных материалов почвы и пожнивных остатков пшеницы
В программном обеспечении EDEM 2021.1 была принята модель Герца–Миндлина для расчета базовых частиц как твердых тел [25]. Эта модель подразделяет контактное движение между частицами на тангенциальное движение и нормальное качение и разлагает силу на параллельную комбинацию тангенциальной и радиальной пружинной демпфирующей системы и эффекта вязкого элемента. Эта модель может более точно отражать эффект сжатия и механические свойства упругого столкновения между почвой и частицами пожнивных остатков [26,27]. Кроме того, модель Герца–Миндлина с JKR-адгезией может моделировать эффекты склеивания и агломерации глинистой почвы, наделяя частицы поверхностной энергией [28]. В связи с этим, в данном исследовании была выбрана модель Герца–Миндлина с JKR-адгезией в качестве контактной модели для моделирования почвы.
3.1. Испытание угла естественного откоса смеси почвы и пожнивных остатков пшеницы
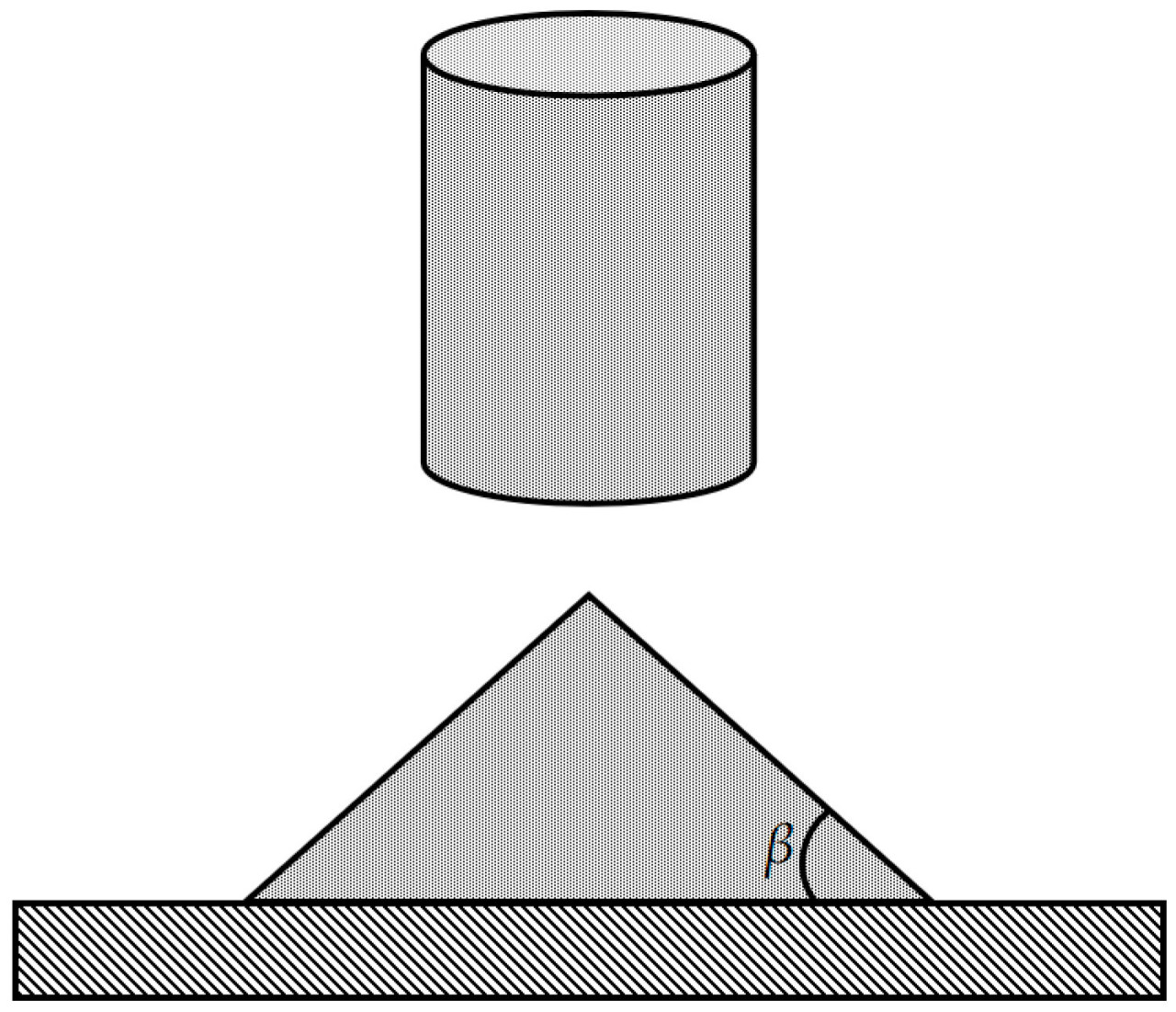
В качестве стандарта для оценки параметров материала угол естественного откоса может напрямую отражать характеристики трения и текучесть между частицами [29]. В данном исследовании угол естественного откоса смеси почвы и пожнивных остатков пшеницы измеряли методом подъема цилиндра. Испытательное устройство состояло из цилиндра из стали 65Mn с внутренним диаметром 60 мм и квадратного основания из стальной плиты 65Mn. До начала эксперимента цилиндр, плотно прилегающий к контактной поверхности основания, заполняли количеством рыхлой смеси почвы и пожнивных остатков пшеницы. Затем цилиндр медленно поднимали до тех пор, пока вся смесь не высыпалась на основание, образовав коническую насыпь. После стабилизации частиц материала с помощью высокоточного универсального уровня измеряли угол β между образующей конуса и горизонтальной плоскостью, то есть угол естественного откоса. Принцип испытания показан на Рисунке 9. Для обеспечения надежности данных эксперимент повторяли пять раз, и результаты представлены в Таблице 7. Средний угол естественного откоса β смеси почвы и пожнивных остатков пшеницы составил 35,12°.
Рисунок 9. Принцип измерения угла естественного откоса.
Таблица 7. Экспериментальные результаты угла естественного откоса для смеси почвы и пожнивных остатков пшеницы.
3.2. Тест Плэкетта–Бермана
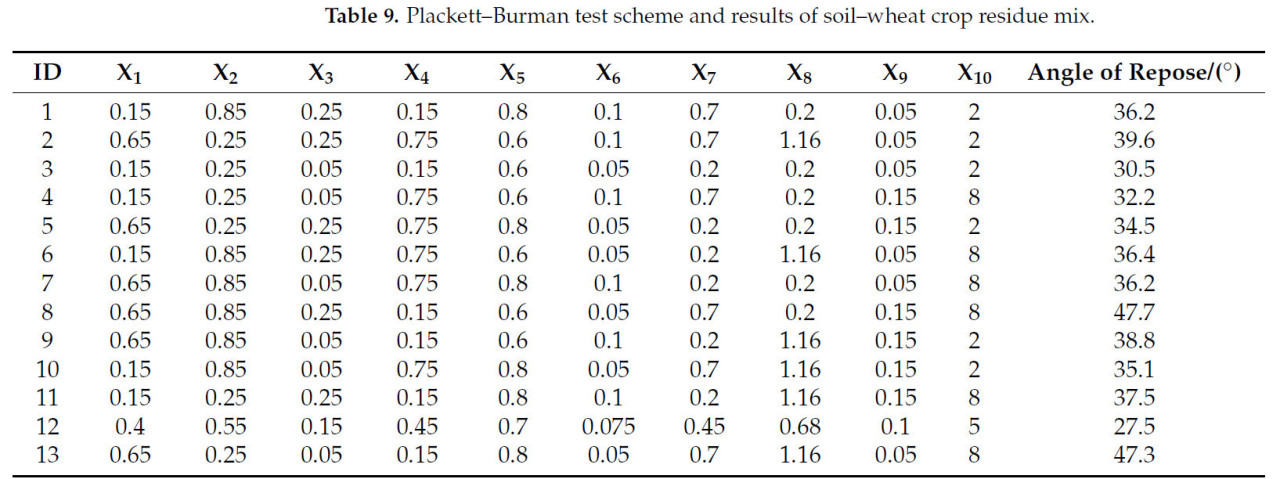
Для обеспечения соответствия между эффектом моделирования насыпи и экспериментальными результатами угол естественного откоса следует использовать в качестве оценочного показателя для точной калибровки параметров модели [30]. Учитывая большое количество неизвестных параметров в процессе моделирования, в данном исследовании сначала использовалось программное обеспечение Design-Expert 13.1.0 для планирования теста Плэкетта–Бермана с целью отсева факторов, оказывающих значительное влияние на процесс моделирования угла естественного откоса [31]. В процессе моделирования угла естественного откоса смеси материалов почвы и пожнивных остатков пшеницы физические параметры между почвой, пожнивными остатками пшеницы и сталью 65Mn были непосредственно определены и взяты из предыдущих испытаний, а параметры их взаимного контакта были выбраны в соответствующем диапазоне для анализа значимости. Поверхностная энергия почвы для модели JKR могла быть взята как справочное значение из базы данных GEMM программного обеспечения EDEM. В Таблице 8 перечислены диапазоны значений параметров теста Плэкетта–Бермана, которые включают 10 влияющих факторов и 1 виртуальный параметр. Конкретная схема испытаний и результаты представлены в Таблице 9.
Таблица 8. Параметры теста Плэкетта–Бермана для смеси почвы и пожнивных остатков пшеницы.
Таблица 9. Схема и результаты теста Плэкетта–Бермана для смеси почвы и пожнивных остатков пшеницы.
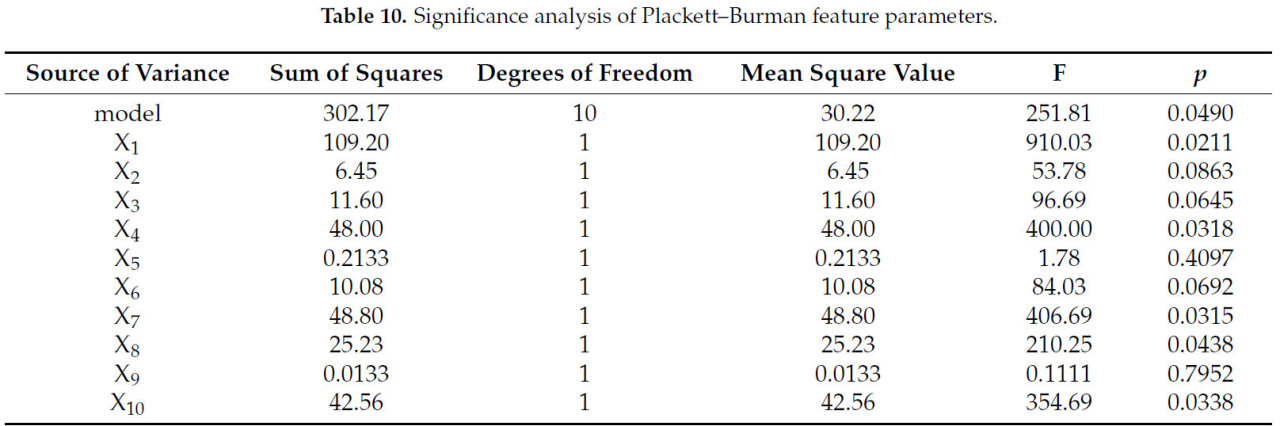
Как показано в Таблице 10, общая модель оказывает значительное влияние. Коэффициент детерминации R² = 0,9996 указывает на то, что тестовая модель подходит для 99,96% тестовых данных. F-критерий модели составляет 251,8, что указывает на значимость модели, а вероятность возникновения такого большого значения F-критерия из-за ошибки составляет всего 4,90%. Значение p меньше 0,05 указывает на то, что фактор значим; при этом условии X1, X4, X7, X8 и X10 являются значимыми факторами, а значение p больше 0,1000 указывает на то, что фактор незначим. Из-за избыточного количества значимых факторов трудно провести многофакторный ортогональный тест. Чтобы сократить анализ влияющих факторов, было обнаружено, что значение F-критерия для X8 меньше, чем для модели, что указывает на незначимость различия на текущем уровне значимости, поэтому для дальнейшей оптимизации и калибровки были выбраны только значимые факторы X1, X4, X7 и X10 для проведения теста наискорейшего подъема [32].
Таблица 10. Анализ значимости характеристических параметров теста Плэкетта–Бермана.
3.3. Планирование теста наискорейшего подъема
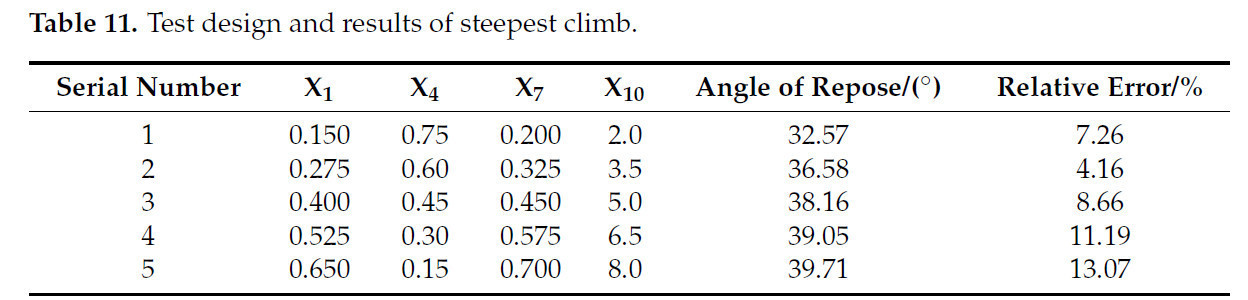
Чтобы определить оптимальные значения высокозначимых факторов (коэффициент восстановления при столкновении почва-почва X1, коэффициент восстановления при столкновении почва-пожнивные остатки пшеницы X4, коэффициент восстановления при столкновении пожнивные остатки-пожнивные остатки пшеницы X7 и поверхностная энергия почвы X10), остальные параметры были установлены на среднем уровне, и был спланирован тест наискорейшего подъема, как показано в Таблице 11 [33]. По мере увеличения значений факторов X1, X4, X7 и X10 угол естественного откоса, полученный в результате имитационных испытаний, постепенно увеличивается, в то время как относительная ошибка угла естественного откоса между имитационными и реальными испытаниями сначала уменьшается, а затем увеличивается. Ошибка в испытании 2 достигла минимального значения, а значение угла естественного откоса в имитационном испытании было немного больше, чем в реальном испытании. Поэтому при последующей установке уровней факторов для теста Бокса–Бенкена был выбран уровень № 2 теста наискорейшего подъема в качестве среднего уровня [34].
Таблица 11. План и результаты испытаний наискорейшего подъема.
3.4. Планирование теста Бокса–Бенкена
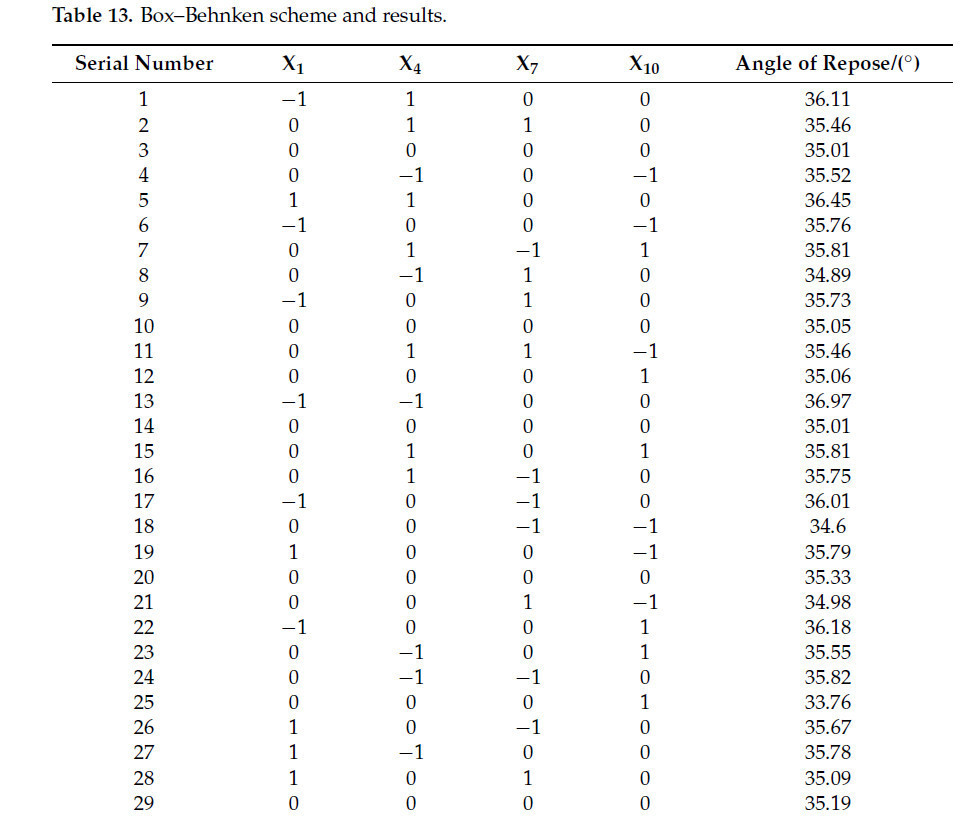
Тест Бокса–Бенкена был спланирован с использованием программного обеспечения Design-Expert, и была получена квадратичная регрессионная модель зависимости угла естественного откоса от X1, X4, X7, X10 и целевого значения [35]. Уровни тестовых факторов показаны в Таблице 12, а схема и результаты испытаний представлены в Таблице 13.
Таблица 12. Параметры теста Бокса–Бенкена для смеси почвы и пожнивных остатков пшеницы.
Таблица 13. Схема и результаты теста Бокса–Бенкена.
Путем множественного регрессионного анализа результатов испытаний была получена модель второго порядка для угла естественного откоса смеси материалов почвы и пожнивных остатков пшеницы и четырех значимых параметров. Уравнение регрессии следующее:
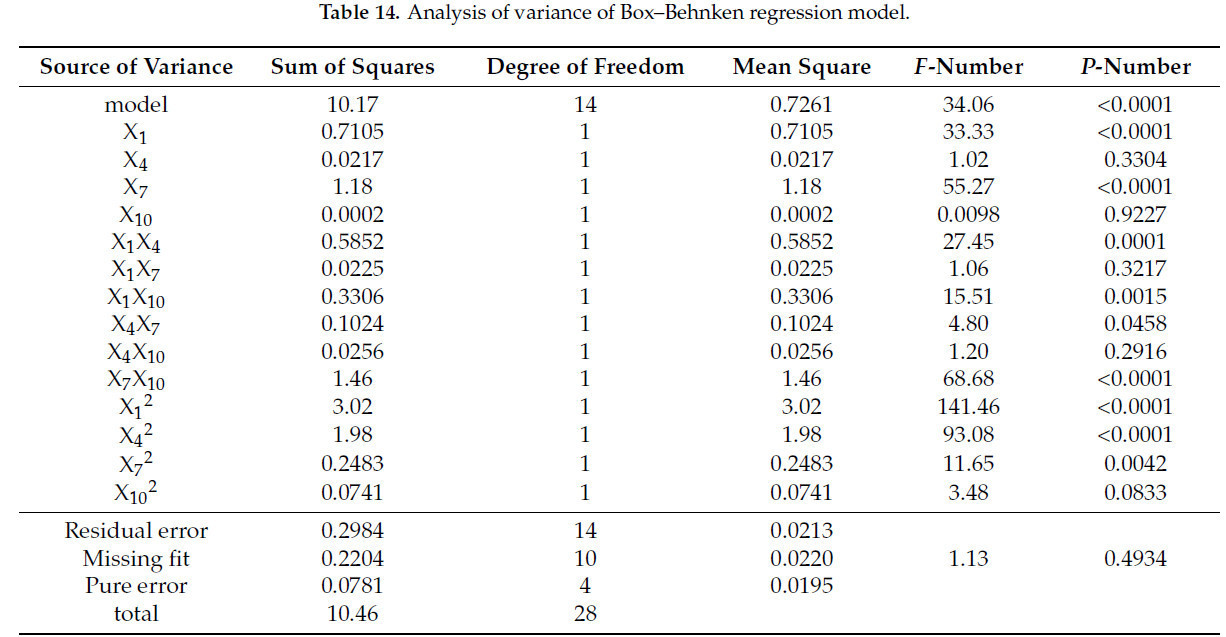
В Таблице 14 показаны результаты дисперсионного анализа (ANOVA) квадратичной полиномиальной регрессионной модели. Значение p этой модели меньше 0,05, что указывает на то, что эта модель весьма значима, а X1, X7, X1X4, X1X10, X4X7, X7X10, X1², X4² и X7² являются значимыми факторами. Коэффициент детерминации R² = 0,9717, скорректированный коэффициент детерминации R²adj = 0,9434, а F-критерий для члена ошибки неадекватности составляет 1,13, что указывает на то, что член ошибки неадекватности незначим по сравнению с чистой ошибкой. Результаты показали, что модель является значимой и надежной и может точно анализировать и прогнозировать ключевые параметры смеси почвы и пожнивных остатков пшеницы.
Таблица 14. Дисперсионный анализ регрессионной модели Бокса–Бенкена.
3.5. Оптимальные наборы параметров и проверка физических характеристик для моделирования смеси почвы и пожнивных остатков пшеницы
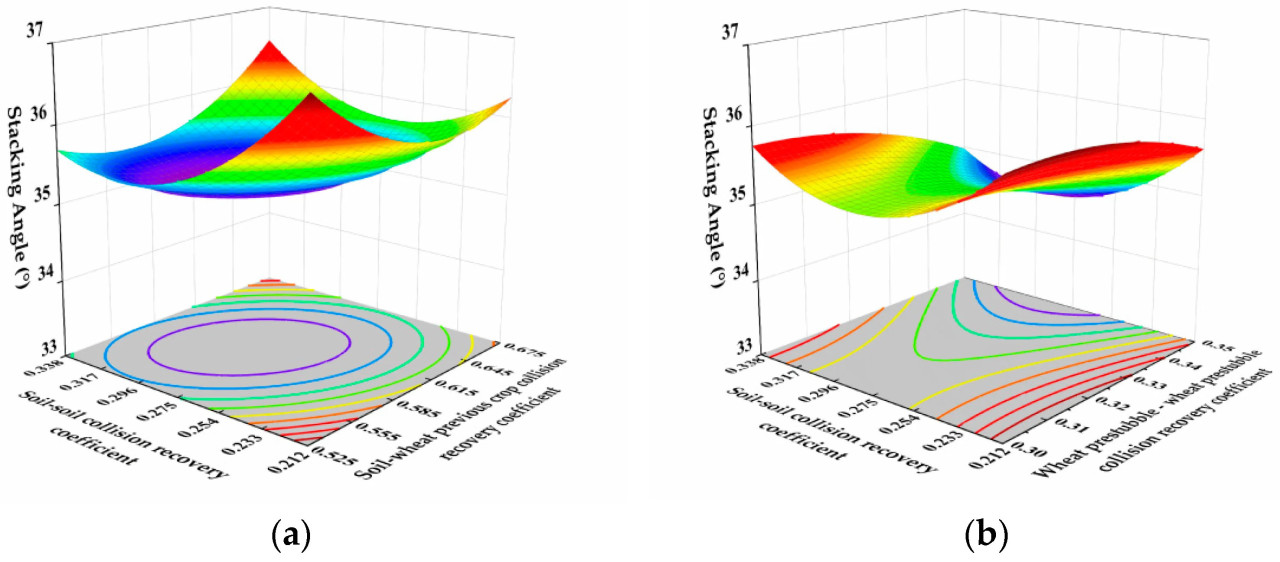
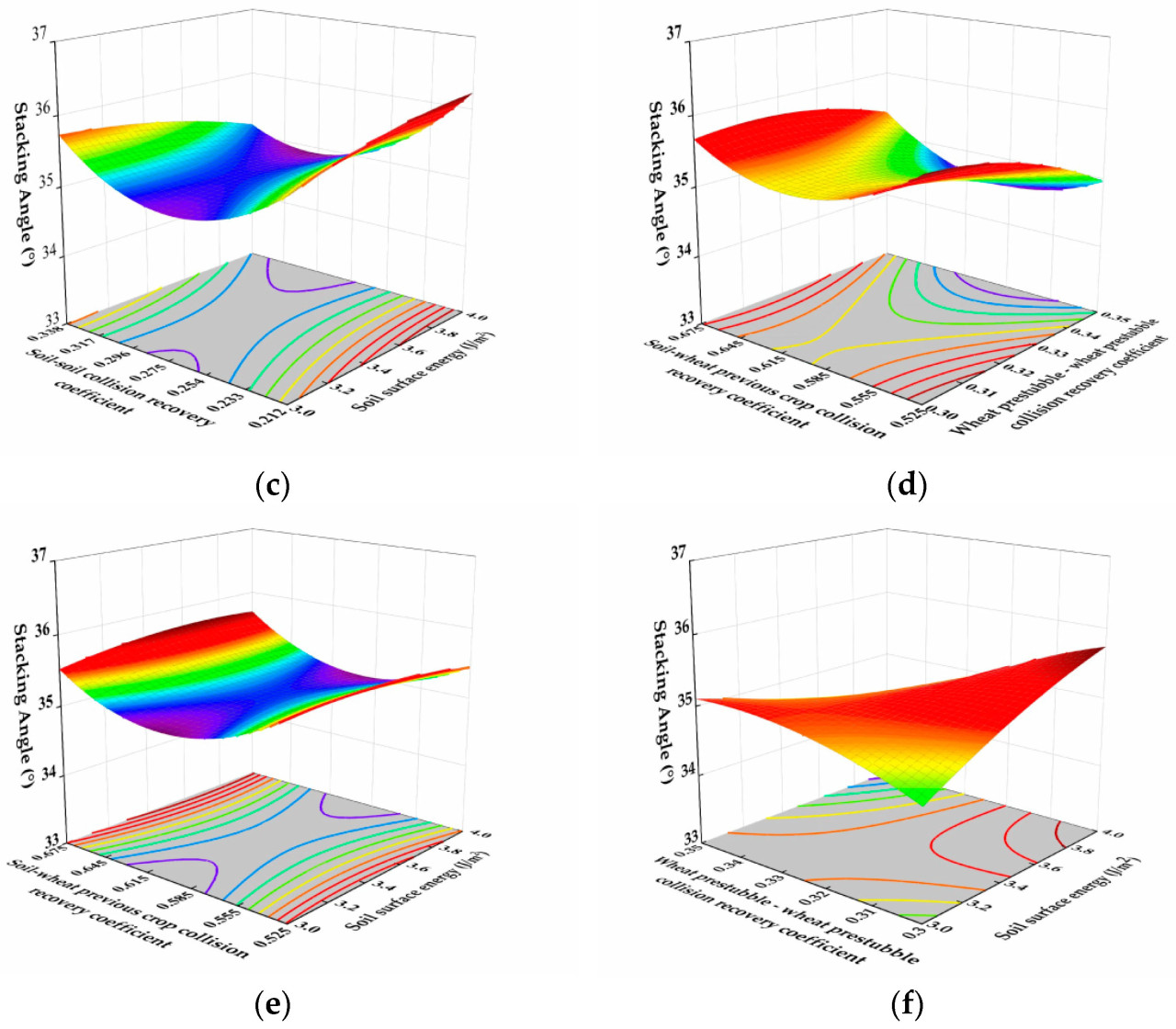
Программное обеспечение Design-Expert было использовано для проведения квадратичного множественного регрессионного анализа данных модели с целью получения диаграммы поверхности отклика взаимодействия между параметрами, влияющими на угол естественного откоса целевой функции, как показано на Рисунке 10. Для факторов X1, X4, X7 и X10 существуют определенные различия в тенденции изменения угла естественного откоса. С увеличением X1 и X4 угол естественного откоса сначала уменьшается, а затем увеличивается, в то время как с увеличением X7 угол естественного откоса уменьшается. С увеличением X10 угол естественного откоса увеличивается.
Рисунок 10. Диаграмма поверхности отклика взаимодействия между параметрами, влияющими на угол естественного откоса. (a) Диаграмма поверхности отклика влияния взаимодействия факторов X1 и X4 на угол естественного откоса. (b) Диаграмма поверхности отклика влияния взаимодействия факторов X1 и X7 на угол естественного откоса. (c) Диаграмма поверхности отклика влияния взаимодействия факторов X1 и X10 на угол естественного откоса. (d) Диаграмма поверхности отклика влияния взаимодействия факторов X4 и X7 на угол естественного откоса. (e) Диаграмма поверхности отклика влияния взаимодействия факторов X4 и X10 на угол естественного откоса. (f) Диаграмма поверхности отклика влияния взаимодействия факторов X7 и X10 на угол естественного откоса.
Модуль числовой оптимизации (Optimization Numerical optimization) в программном обеспечении Design-Expert был использован для оптимизации параметров, влияющих на угол естественного откоса смеси материалов почвы и пожнивных остатков пшеницы, и было успешно получено 49 групп оптимальных решений. Эти оптимальные решения были проверены с помощью имитационных испытаний и, по сравнению с фактическим углом естественного откоса, было окончательно определено оптимальное решение для угла естественного откоса [36]. В этот момент оптимальная комбинация параметров для смеси почвы и пожнивных остатков пшеницы была следующей: коэффициент восстановления при столкновении почва-почва составил 0,237, коэффициент восстановления при столкновении почва-пожнивные остатки пшеницы — 0,311, коэффициент восстановления при столкновении пожнивные остатки-пожнивные остатки пшеницы — 0,575, а поверхностная энергия почвы — 3,94 Дж/м². При этих параметрах угол естественного откоса смеси почвы и пожнивных остатков пшеницы составляет 35,38°, а относительная ошибка по сравнению с измеренным средним углом естественного откоса 35,12° составляет 0,74%. Как показано на Рисунке 11, сравнивая угол естественного откоса измеренной смеси почвы и пожнивных остатков пшеницы с результатами имитационного испытания, было обнаружено, что между ними нет значительного различия в угле естественного откоса и форме, что указывает на высокую точность настройки параметров моделирования [37].
Рисунок 11. Испытание угла естественного откоса почвы. (a) Полевое испытание; (b) имитационное испытание.
4. Проверка испытаний
Для проверки обоснованности параметров моделирования были проведены эксперименты, в которых в качестве тестовых показателей использовались ровность поверхности и степень покрытия пожнивными остатками пшеницы.
4.1. Имитационное испытание
Как показано на Рисунке 12, была выбрана оптимальная комбинация параметров для смеси почвы и пожнивных остатков пшеницы. В EDEM была создана частицовая подушка смеси почвы и пожнивных остатков пшеницы размером 3600 мм × 2500 мм × 300 мм (длина, ширина, высота) для имитационных испытаний. Физические параметры были получены из предыдущих экспериментов и ссылок, а контактные параметры, за исключением значимых, были взяты как средние значения предыдущих результатов измерений. Данные представлены в Таблице 15 и Таблице 16.
Рисунок 12. Частицовая подушка для имитационного испытания.
Таблица 15. Физические параметры моделирования смеси почвы и пожнивных остатков пшеницы.
Таблица 16. Контактные параметры имитационного испытания для смеси почвы и пожнивных остатков пшеницы.
4.1.1. Имитационное испытание ровности поверхности
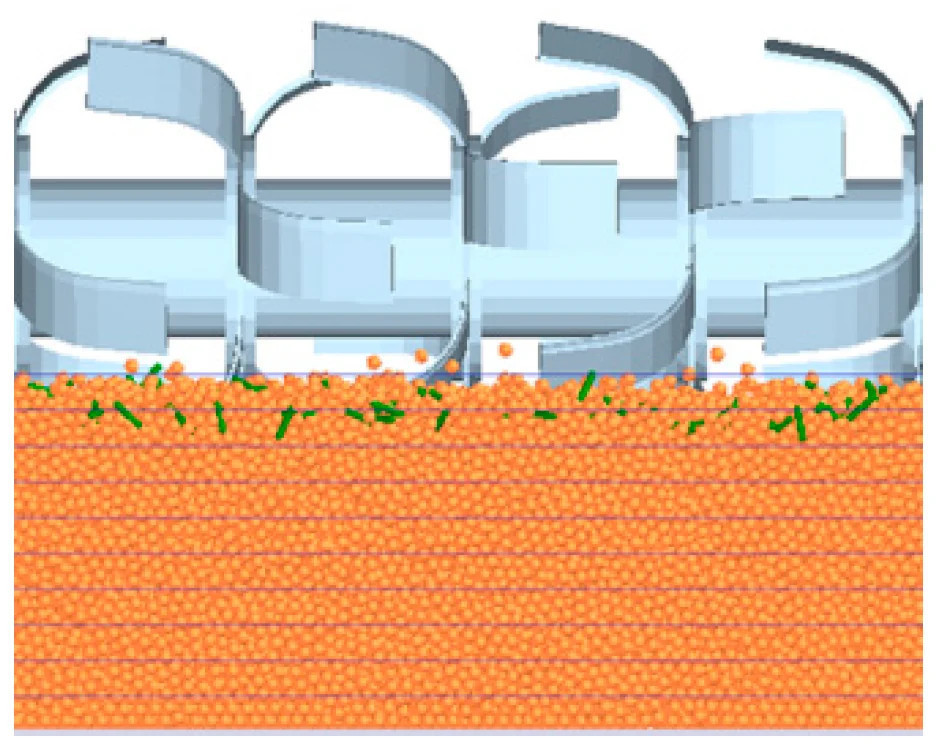
После моделирования выбирается поперечное сечение моделирования, перпендикулярное направлению движения фрезы, как показано на Рисунке 13. В этом разделе используется функция разбиения на сетку модуля Grid Bin Group программного обеспечения EDEM2021.1, и высота сетки установлена на 30 мм. Согласно GB T5668-2017; Стандарт качества для работы фрезерного культиватора. Администрация стандартизации Китая: Пекин, Китай, 2017. Наблюдая за поперечным сечением имитационного испытания, было обнаружено, что контуры поверхности смоделированной почвы находятся в верхней ячейке сетки, то есть ровность поверхности составляет менее 30 мм, и операция фрезерной обработки соответствует текущему китайскому стандарту ровности поверхности менее 50 мм после фрезерной обработки [38].
Рисунок 13. Поперечное сечение имитационного моделирования ровности поверхности.
4.1.2. Имитационное испытание степени покрытия соломой
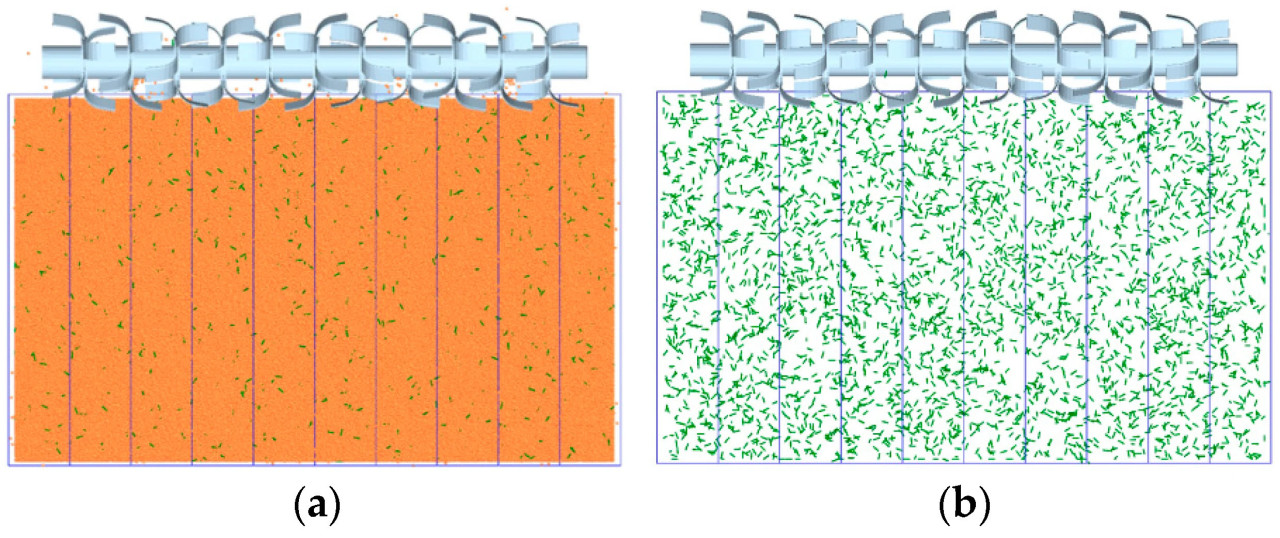
Как показано на Рисунке 14a, после моделирования поверхность частицовой подушки была разделена на 10 секций в поперечном направлении. Были случайным образом выбраны пять секций, и в каждой секции вручную подсчитывали пожнивные остатки пшеницы, обнаженные на поверхности подушки. Затем подсчитывали все пожнивные остатки пшеницы в соответствующих секциях, как показано на Рисунке 14b, и рассчитывали степень покрытия пожнивными остатками пшеницы. Результаты представлены в Таблице 17.
Рисунок 14. Поперечное сечение имитационного моделирования покрытия пожнивными остатками пшеницы. (a) Поверхность частицовой подушки после моделирования; (b) распределение частиц пожнивных остатков пшеницы после скрытия частиц почвы.
Таблица 17. Статистические результаты имитационного эксперимента по степени укрытия соломой.
4.2. Полевые испытания
Полевой эксперимент проводился на демонстрационной базе сельскохозяйственных испытаний на засоленных почвах сельскохозяйственной высокотехнологичной зоны Хуантреугольник, город Дунъин, провинция Шаньдун. Силовой установкой всего агрегата был трактор JM1854 производства Shandong Juming Machinery Co, Ltd., Цзыбо, Китай, который был соединен с фрезерным культиватором 1 GKN-350 K производства Henan Haofeng Agricultural Equipment Co, Ltd., Сюйчан, Китай. Скорость движения испытательного агрегата была установлена на 2 км/ч, а скорость ВОМ трактора составляла 750 об/мин. Испытательное оборудование включало рулетку, стальные пластины с зубьями, электронные весы, рамку для почвы и т.д. Место испытания показано на Рисунке 15.
Рисунок 15. Полевые испытания.
4.2.1. Полевые испытания ровности поверхности
В направлении, перпендикулярном движению агрегата, мы взяли горизонтальную базовую линию, длина которой равнялась ширине захвата машины в самой высокой точке поверхности, в качестве ориентира, разделили ее на 10 равных точек, измерили расстояние от каждой точки до поверхности и взяли среднее значение в качестве результата для одного прохода. Всего было протестировано 5 проходов. Стандартное отклонение рассчитывается по формулам (22) и (23), а ровность представлена средним стандартным отклонением. Результаты представлены в Таблице 18.
где Zi — высота точки измерения поверхности грунта, см; N — количество точек; Z — средняя высота точек измерения поверхности, см; Sb — стандартное отклонение ровности поверхности, см.
Таблица 18. Результаты испытаний ровности поверхности.
4.2.2. Полевые испытания степени покрытия соломой
В исследуемой области по диагонали было выбрано пять точек отбора проб, и на каждой точке отбирали пробу на площади 1 м². Затем измеряли массу собранных образцов пожнивных остатков пшеницы и рассчитывали массу пожнивных остатков пшеницы в пяти точках отбора проб на основе данных. Наконец, согласно формуле (24), была рассчитана степень покрытия пожнивными остатками пшеницы. Результаты представлены в Таблице 19.
где Fb — степень покрытия пожнивными остатками пшеницы, %; mq — среднее значение пожнивных остатков пшеницы до обработки, кг; mh — среднее значение пожнивных остатков пшеницы после обработки, кг.
Таблица 19. Результаты полевых испытаний по степени заделки соломы.
4.3. Результаты и анализ
Сравнение полевого эксперимента и имитационного эксперимента показало, что смоделированные и измеренные средние значения ровности поверхности находятся в пределах 30 мм, что соответствует текущему китайскому стандарту ровности поверхности не более 50 мм после обработки фрезерным культиватором. Ошибка между измеренным значением и смоделированным значением степени покрытия пожнивными остатками пшеницы составила 1,34%, что находится в допустимых пределах. Результаты показывают, что характеристические параметры смеси почвы и пожнивных остатков пшеницы в имитационных испытаниях в основном совпадают с таковыми в полевых экспериментах. Метод калибровки параметров дискретно-элементного моделирования для почвы и пожнивных остатков пшеницы на засоленных прибрежных почвах является надежным и точным.
5. Выводы
(1) Были измерены физические параметры почвы и пожнивных остатков пшеницы: средняя плотность почвы составила 2,18 × 10³ кг/м³, влажность почвы — 21,79%, коэффициент Пуассона — 0,32, модуль сдвига — 1,2 × 10⁶ кПа, а средняя плотность пожнивных остатков пшеницы — 241 кг/м³. Были измерены параметры трения и коэффициенты восстановления при столкновении для смеси почвы и пожнивных остатков пшеницы.
(2) Принимая угол естественного откоса в качестве переменной отклика, с помощью теста Плэкетта–Бермана были отобраны факторы, оказывающие весьма значительное влияние на угол естественного откоса: коэффициент восстановления при столкновении почва-почва X1, коэффициент восстановления при столкновении почва-пожнивные остатки пшеницы X4, коэффициент восстановления при столкновении пожнивные остатки-пожнивные остатки пшеницы X7 и поверхностная энергия JKR почвы X10. На основе этого для определения оптимального диапазона значений этих высокозначимых факторов дальнейшим образом использовались тест наискорейшего подъема и тест Бокса–Бенкена, и была установлена квадратичная регрессионная модель между углом естественного откоса и значимыми факторами. Модуль числовой оптимизации программного обеспечения Design-Expert был использован для оптимизации параметров угла естественного откоса смеси почвы и пожнивных остатков пшеницы, и было успешно получено 49 наборов оптимальных решений. Эти оптимальные решения были проверены с помощью имитационных испытаний и сравнены с фактическим углом естественного откоса. В итоге были определены оптимальные значения значимых параметров. Результаты измерений подробно описаны в Таблице 16 предыдущего текста.
(3) Точность калибровки параметров моделирования была подтверждена путем сравнения результатов полевого эксперимента по фрезерной обработке и имитационного эксперимента. Результаты показывают, что как смоделированное значение, так и измеренное среднее значение ровности поверхности находятся в пределах 30 мм, что соответствует текущему стандарту ровности поверхности менее 50 мм после обработки фрезерным культиватором в Китае. Ошибка между измеренными и смоделированными значениями степени покрытия пожнивными остатками пшеницы составляет 1,34%, что находится в допустимых пределах. Результаты показывают, что метод калибровки параметров дискретно-элементного моделирования для почвы и пожнивных остатков пшеницы на засоленных прибрежных почвах является осуществимым.
(4) Данное исследование может точно отражать реальные механические взаимосвязи, такие как трение и адгезия между частицами почвы, а смоделированная деформация почвы, смещение и изменение пор высоко соответствуют реальным полевым условиям. При обработке и подготовке почвы на засоленных землях сельскохозяйственная техника сталкивается с такими проблемами, как высокое сопротивление, легкое погружение, трудность крошения почвы и намотка пожнивных остатков пшеницы. После точной калибровки параметров моделируется взаимодействие между почворазрушающими и противостерневыми рабочими органами оборудования для обработки почвы и засоленной почвой с пожнивными остатками пшеницы. На основе этого оптимизируется конструкция для снижения энергозатрат при работе и повышения адаптируемости и производительности сельскохозяйственной техники в засоленных условиях.
Ссылки
1. Pan, T.L. Effects of Straw Return on Carbon Sequestration in CoastalSaline-Sodic Soils. Master’s Thesis, Shandong Agricultural University, Tanan, China, 2024. [Google Scholar]
2. Shi, R.J.; Dai, F.; Zhao, W.Y.; Zhang, F.W.; Shi, L.R.; Guo, J.H. Establishment of discrete element flexible model and verification of contact parameters of flax stem. Trans. Chin. Soc. Agric. Mach. 2022, 53, 146–155. [Google Scholar]
3. Song, S.L.; Tang, Z.H.; Zhang, X.; Liu, J.B.; Meng, X.J.; Liang, Y.C. Calibration of the discrete element parameters for the soil model of cotton field after plowing in Xinjiang of China. Trans. Chin. Soc. Agric. Eng. 2021, 37, 63–70. [Google Scholar]
4. Zhou, H.; Che, H.L.; Geng, D.Y.; Chen, M.Z.; Zhang, Y.P. Discrete element modeling and parameter calibration of typical soil in maize fieldtillage layer. Chin. Soc. Agric. Mach. 2023, 54, 49–60. [Google Scholar]
5. Zhao, Z.H.; Wu, M.L.; Xie, S.P.; Luo, H.F.; Li, P.C.; Zeng, Y.; Jiang, X.H. Parameter calibration for the discrete element simulation of soil-preceding rice stubble and its rotary tillage trajectory. Trans. Chin. Soc. Agric. Eng. 2024, 40, 72–82. [Google Scholar]
6. Xia, J.F.; Zhang, P.; Yuan, H.W.; Du, J.; Zheng, K.; Li, Y.F. Calibration and Verification of Flexible Rice Straw Model by Discrete Element Method. Chin. Soc. Agric. Mach. 2024, 55, 174–184. [Google Scholar]
7. Tian, X.L.; Cong, X.; Qi, J.T.; Guo, H.; Li, M.; Fan, X.H. Parameter calibration of discrete element model of corn straw-soil mixturein black soil areas. Chin. Soc. Agric. Mach. 2021, 52, 100–108. [Google Scholar]
8. Wang, D.W.; Lu, T.; Zhao, Z.; Shang, S.Q.; Zheng, S.; Liu, J. Calibration of Discrete Element Simulation Parameters for Cultivated Soil Layer inCoastal Saline alkali Soil. Chin. Soc. Agric. Mach. 2024, 55, 240–249. [Google Scholar]
9. Shan, H.Y.; Yan, Y.N.; Liu, X.J.; Zhang, J.; Han, X.; Shi, L.; Liu, J.; Shen, Y. Calibration of discrete element parameters in wheat-corn farming strawmixed soil returning mode. Agric. Eng. 2024, 14, 72–81. [Google Scholar]
10. Zhang, B.; Yang, X.S.; Wang, J.Y.; Chen, J.; Shen, W.M. Construction of a rheological model based on discrete element parameterscalibration of clay from sugarcane cultivated land. Trans. Chin. Soc. Agric. Eng. 2024, 40, 36–44. [Google Scholar]
11. Shi, L.R.; Zhao, W.Y.; Sun, W. Parameter calibration of soil particles contact model of farmland soil in northwest aridregion based on discrete element method. Trans. Chin. Soc. Agric. Eng. 2017, 33, 181–187. [Google Scholar]
12. Wu, Z.Y. Research on Tillage Resistance of Double-wing Subsoiler Based on Discrete Element Method. Master’s Thesis, Hunan Agricultural University, Changsha, China, 2021. [Google Scholar]
13. Xiang, W.; Wu, M.L.; Lv, J.N.; Quan, W.; Ma, L.; Liu, J.J. Calibration of simulation physical parameters of clay loam based on soil accumulation test. Trans. Chin. Soc. Agric. Eng. 2019, 35, 116–123. [Google Scholar]
14. Liu, F.Y. Discrete Element Modelling of the Wheat Particles and Short Straw in Cleaning Devices. Ph.D. Thesis, Northwest A&F University, Yangling, China, 2018. [Google Scholar]
15. Zhou, H.; Zhang, J.M.; Zhu, Y.H.; Zhang, C.L.; Tahir, H.M.; Xia, J.F. Design and experiment of combined tillage machine for subsoiling and rotary burying of straw incorporated into soil. Trans. Chin. Soc. Agric. Eng. 2017, 33, 17–26. [Google Scholar]
16. Fang, H.M. Research on the Straw-Soil-Rotary Blade Interaction Using Discrete Element Method. Ph.D. Thesis, Nanjing Agricultural University, Nanjing, China, 2016. [Google Scholar]
17. Pan, H.R. Design and Parameter Optimization of Biaxial Rotary Stubble Machine Based on Discrete Element. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2020. [Google Scholar]
18. He, Y.M.; Xiang, W.; Wu, M.L.; Quan, W.; Chen, C.P. Parameters calibration of loam soil for discrete element simulation based on the repose angle of particle heap. J. Hunan Agric. Univ. Nat. Sci. 2018, 44, 216–220. [Google Scholar]
19. Diao, H.L.; Zhang, Y.P.; Diao, P.S.; Zhao, N. Design and experiment of a no-tillage and wide band wheat planter with subsoilsbased on EDEM. J. Agric. Mech. Res. 2017, 39, 58–62. [Google Scholar]
20. Liao, Q.X.; Xie, H.M.; Zhang, Q.S.; Zhang, J.Q.; Ao, Q.; Wang, L. Design and experiment of driven disc plow and double-edged rotary tillagecombined tiller. Chin. Soc. Agric. Mach. 2023, 54, 99–110. [Google Scholar]
21. Li, J.W.; Tong, J.; Hu, B.; Wang, H.B.; Mao, C.Y.; Ma, Y.H. Calibration of parameters of interaction between clayey black soil with different moisture content soil-engaging component northeast China. Trans. Chin. Soc. Agric. Eng. 2019, 35, 130–140. [Google Scholar]
22. Zhou, H.; Li, D.; Liu, Z.Y.; Li, Z.Y.; Luo, S.C.; Xia, J.F. Simulation and experiment of spatial distribution effect after straw incorporation into soil by rotary burial. Trans. Chin. Soc. Agric. Mach. 2019, 50, 69–77. [Google Scholar]
23. Wang, X.L.; Hu, H.; Wang, Q.J.; Li, H.W.; He, J.; Chen, W.Z. Calibration method of soil contact characteristic parameters based on DEM theory. Trans. Chin. Soc. Agric. Mach. 2017, 48, 78–85. [Google Scholar]
24. Song, Z.H.; Li, H.; Yan, Y.F.; Tian, F.Y.; Li, Y.D.; Li, F.D. Calibration method of contact characteristic parameters of soil in mulberryfield based on unequal-diameter particles DEM theory. Chin. Soc. Agric. Mach. 2022, 53, 21–33. [Google Scholar]
25. Sun, J.B.; Liu, Q.; Yang, F.Z.; Liu, Z.J.; Wang, Z. Calibration of discrete element simulation parameters of sloping soil onLoess Plateau and its interaction with rotary tillage components. Chin. Soc. Agric. Mach. 2022, 53, 63–73. [Google Scholar]
26. Zeng, Z.W.; Ma, X.; Cao, X.L.; Li, Z.H.; Wang, X.C. Critical review of applications of discrete element method in agricultural engineering. Chin. Soc. Agric. Mach. 2021, 52, 1–20. [Google Scholar]
27. Yu, W.; Liu, R.; Yang, W. Parameter Calibration of Pig Manure with Discrete Element Method Based on JKR Contact Model. AgriEngineering 2020, 2, 367–377. [Google Scholar] [CrossRef]
28. Zhao, J.Z. Simulation and Experimental Investigation of Potato Digging Shovel Working Resistance Based on Discrete Element Method. Master’s Thesis, Shenyang Agricultural University, Shenyang, China, 2017. [Google Scholar]
29. Zhang, R.; Han, D.L.; Ji, Q.L.; He, Y.; Li, J.Q. Calibration methods of sandy soil parameters in simulation of discrete element method. Trans. Chin. Soc. Agric. Mach. 2017, 48, 49–56. [Google Scholar]
30. Zhang, C.; Fan, X.H.; Li, M.S.; Li, G.; Zhao, C.K.; Sun, W.L. Simulation analysis and experiment of soil disturbance by chisel plow based on EDEM. Chin. Soc. Agric. Mach. 2022, 52, 52–59. [Google Scholar]
31. Jiang, Y.X.; Qu, H.; Liu, X.F.; Zhang, H.C.; ZHOU, X.; Zhang, L. Design and Simulation of Spade Tooth Film Lifting Device for Residual Film Recycling Machine. Chin. Soc. Agric. Mach 2024, 12, 1–10. [Google Scholar]
32. Dai, F.; Song, X.F.; Zhao, W.Y.; Zhang, F.W.; Ma, H.j.; Ma, M.Y. Simulative calibration on contact parameters of discrete elements for covering soil on whole plastic film mulching on double ridges. Chin. Soc. Agric. Mach. 2019, 50, 49–56. [Google Scholar]
33. Wang, W.W.; Zhu, C.X.; Chen, L.Q.; Li, Z.D.; Huang, X.; Li, J.C. Design and experiment of active staw-removing anti-blocking device for maize no-tillage planter. Trans. Chin. Soc. Agric. Eng. 2017, 33, 10–17. [Google Scholar]
34. Wang, F.A.; Wen, B.; Xie, X.H.; Xie, K.T.; Guo, S.W.; Zhang, Z.G. Operation mechanism analysis and parameter optimization of conveying and separating device of Panax Notoginseng harvester. Chin. Soc. Agric. Mach. 2023, 54, 201–211. [Google Scholar]
35. Lu, Q.; Liu, F.J.; Liu, L.J.; Liu, Z.J.; Liu, Y.Q. Establishment and verification of discrete element model for seed furrow soil—seed—covering device. Chin. Soc. Agric. Mach. 2023, 54, 46–57. [Google Scholar]
36. Xie, W.; Peng, L.; Jiang, P.; Meng, D.X.; Wang, X.S. Discrete element model building and optimization of double-layer bonding of rapeshoots stems at harvest stage. Trans. Chin. Soc. Agric. Eng. 2023, 54, 112–120. [Google Scholar]
37. Wang, W.Z.; Liu, W.R.; Yuan, L.H.; Qu, Z.; He, X.; Lv, Y.L. Simulation and experiment of single longitudinal axial material movement and establishment of wheat plants model. Chin. Soc. Agric. Mach. 2020, 51, 170–180. [Google Scholar]
38. Zhang, X.M. Tudy on Working Mechanism and Experimental of Rotary Tiller for High Straw Returning. Ph.D. Thesis, Huazhong Agricultural University, Wuhan, China, 2017. [Google Scholar]
Liu J, Lu T, Zheng S, Tian Y, Han M, Tai M, He X, Li H, Wang D, Zhao Z. Parameter Calibration Method for Discrete Element Simulation of Soil–Wheat Crop Residues in Saline–Alkali Coastal Land. Agriculture. 2025; 15(2):129. https://doi.org/10.3390/agriculture15020129
Перевод статьи «Parameter Calibration Method for Discrete Element Simulation of Soil–Wheat Crop Residues in Saline–Alkali Coastal Land» авторов Liu J, Lu T, Zheng S, Tian Y, Han M, Tai M, He X, Li H, Wang D, Zhao Z., оригинал доступен по ссылке. Лицензия: CC BY. Изменения: переведено на русский язык.
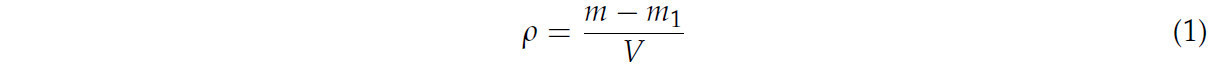


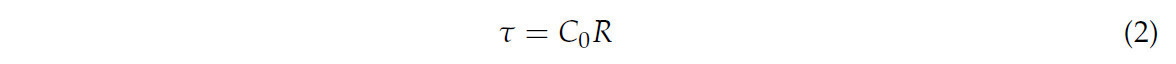
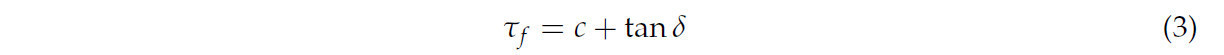

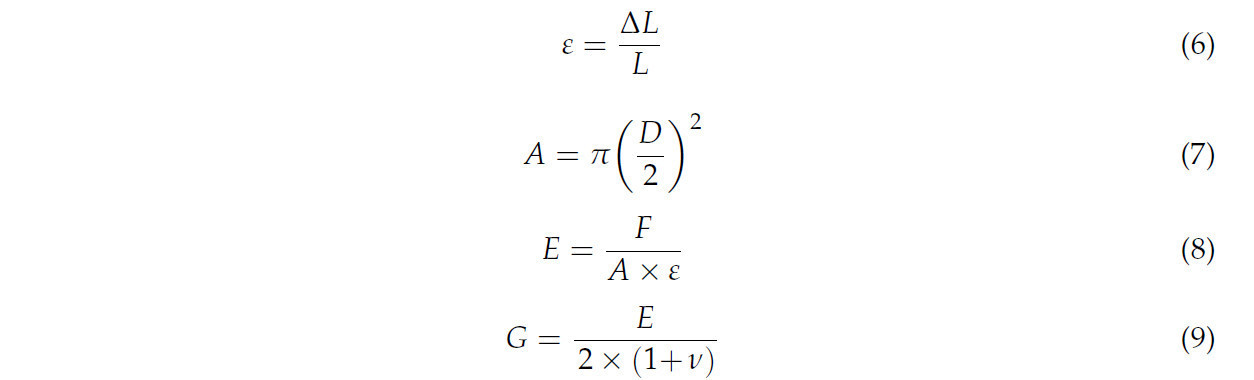


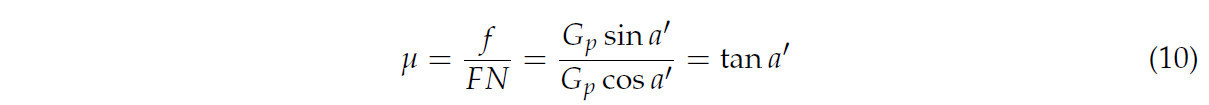

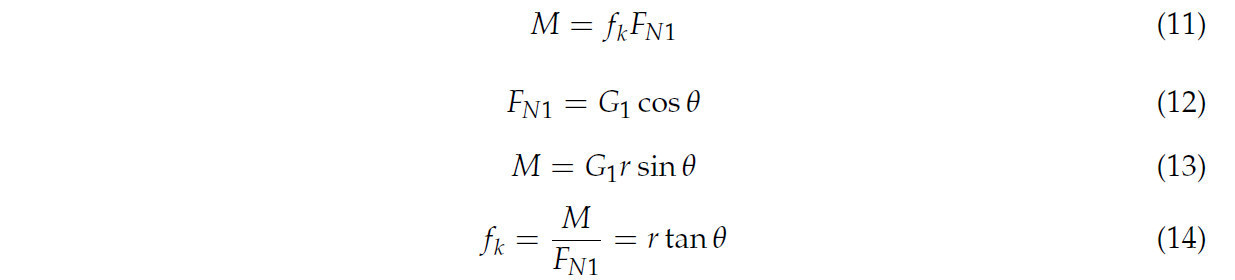

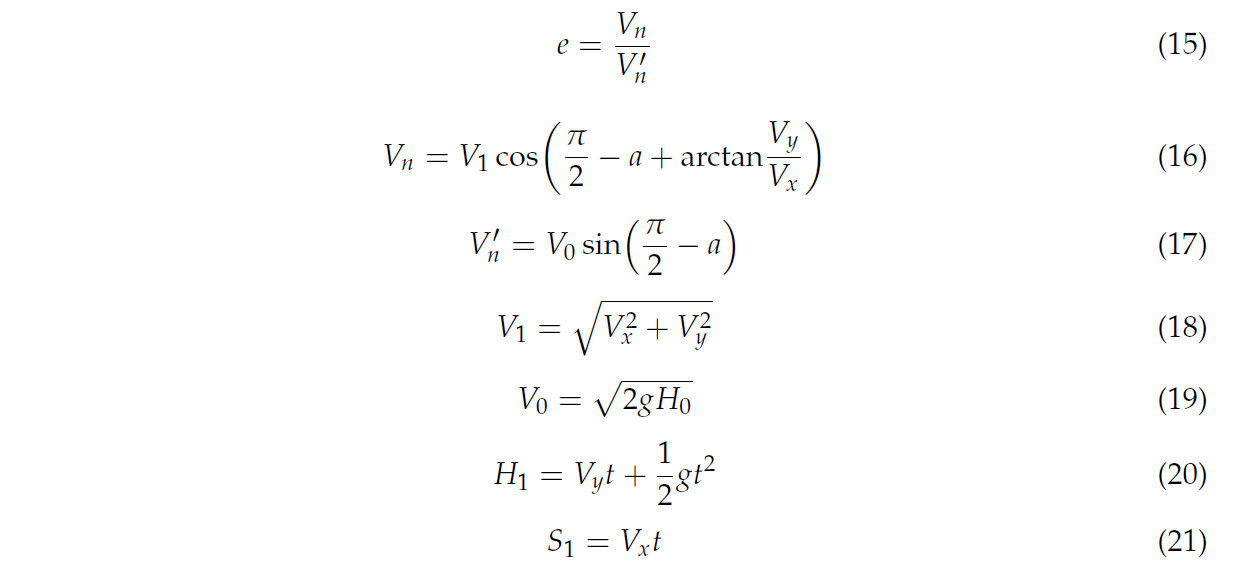




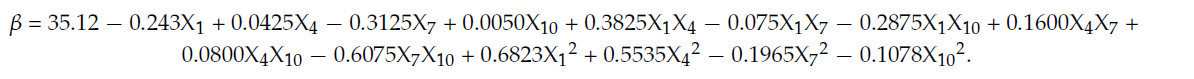






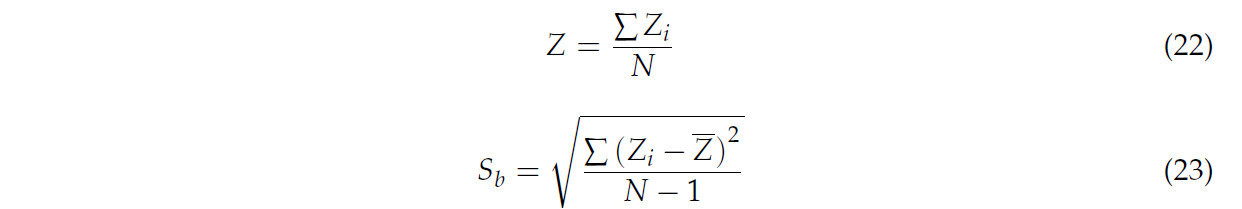

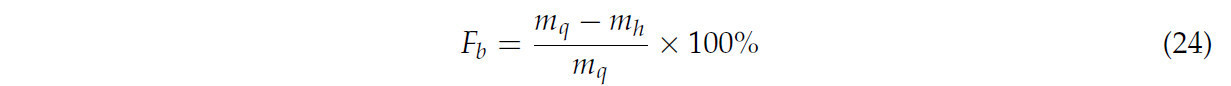































































































Комментарии (0)