Проектирование устройства для обработки соломы для скоростного посева: как математическая модель помогает фермерам
Из-за высокой плотности растительных остатков в районе Хуан-Хуай-Хай в процессе беспахотного посева при скоростных режимах возникают такие проблемы, как высокое сопротивление, увеличенное энергопотребление и обратная засыпка соломы. В данной статье представлена конструкция устройства для обработки соломы, предназначенного для решения этих проблем. Режущая кромка соломорезательного диска оптимизирована с использованием эвольвентной кривой, а ключевые конструктивные параметры устройства определены на основе анализа процесса срезания и удаления стерни.
Аннотация
В данном исследовании для построения моделей уплотненной почвы и полой, гибкой пшеничной соломы был использован метод дискретных элементов (МДЭ), что заложило основу для комплексной модели взаимодействия между рабочим органом, почвой и соломой. В качестве ключевых экспериментальных переменных были выбраны рабочая скорость, частота вращения и межосевое расстояние установки. В качестве оценочных показателей использовались энергопотребление соломорезательного диска (PCD) и коэффициент удаления соломы (SCR).
С помощью метода поверхности отклика и программного обеспечения Design-Expert 12 были разработаны регрессионные модели, связывающие экспериментальные факторы с оценочными показателями. Статистическая значимость оценивалась с помощью дисперсионного анализа (ANOVA, p < 0,05), а взаимодействие факторов анализировалось с помощью анализа поверхности отклика.
Были определены оптимальные эксплуатационные параметры: рабочая скорость 14 км/ч, частота вращения 339,2 об/мин и межосевое расстояние установки 100 см. Результаты моделирования хорошо согласовывались с прогнозируемыми значениями: погрешность составила 1,59% для SCR и 9,68% для PCD. Полевые испытания показали SCR на уровне 86,12%, улучшенную проходимость машины и благоприятные условия для появления всходов.
Данное исследование представляет ценную основу для дальнейшей оптимизации параметров и разработки компонентов.
1. Введение
Технология беспахотного посева играет ключевую роль в улучшении качества почвы и повышении урожайности сельскохозяйственных культур [1,2,3,4,5]. В районе Хуан-Хуай-Хай плотный слой соломы на полях в сочетании с коротким окном посева последующих культур приводит к забиванию сеялки, если солома не управляется должным образом и своевременно. Это забивание может негативно повлиять как на точность высева, так и на проходимость машины [6,7]. В процессе высокоскоростного посева взаимодействие между рабочим органом, соломой и почвой является более сложным, что увеличивает трудность обработки соломы и рабочее сопротивление. Таким образом, ключевой задачей при высокоскоростной работе является снижение сопротивления и энергопотребления, обеспечивая упорядоченное управление соломой.
Для смягчения проблем забивания при беспахотном посеве многочисленные исследователи изучали и внедряли передовые технологии. Одно из предложенных решений включает комбинирование активных и пассивных компонентов для достижения эффективного резания на основе принципа поддерживаемого резания. Этот подход улучшает проходимость машины, снижает рабочее энергопотребление и повышает качество работы, что подтверждается увеличением частоты резания [8,9,10]. Дополнительно, выемчатые дисковые ножи, спроектированные с использованием биомиметических принципов, продемонстрировали отличные показатели в разрезании соломы и почвы [11,12]. Однако большая ширина частей, контактирующих с почвой, может увеличивать сопротивление и энергопотребление при различных рабочих скоростях, приводя к значительному нарушению структуры почвы. Более того, работа на более высоких скоростях усиливает движение соломы и почвы, что приводит к обратной засыпке соломы на семенное ложе и снижению коэффициента удаления соломы (SCR) [13,14,15]. Поэтому использование меньшей ширины обработки является более благоприятным для высокоскоростных операций. Одновременно, при обильном количестве соломы этот подход обеспечивает эффективное разрезание соломы и гарантирует, что очищенная полоса посева достигнет оптимальных показателей посева.
Метод дискретных элементов (DEM), первоначально представленный Кандаллом, является численным подходом, используемым для моделирования поведения сыпучих материалов. С развитием вычислительной техники DEM продемонстрировал значительную эффективность в применении в сельскохозяйственной технике [16,17]. Сравнительный анализ между экспериментами в почвенном лотке и моделированием подтвердил применимость DEM в сельскохозяйственных условиях [18]. Li и др. [19] использовали DEM для моделирования динамических взаимодействий между соломой и компонентами машины, показывая влияние рабочей ширины на силу сопротивления. Путем моделирования взаимодействий между соломой, почвой и техникой DEM предоставил существенную поддержку данными для оптимизации ключевых компонентов и углубления понимания рабочих механизмов, тем самым значительно повысив точность и эффективность исследований [20,21,22,23,24]. Во время полевых операций эти компоненты непосредственно взаимодействуют с почвой и соломой, поднимая и обрабатывая их для достижения эффективной очистки. Энергопотребление и производительность этих компонентов могут заметно различаться при различных рабочих параметрах, что может быть эффективно оценено с использованием DEM. Zhang и др. [25] использовали DEM для построения модели взаимодействия, улучшая точность моделирования. Анализируя влияние различных параметров, которые минимизировали нарушение почвы и повышали эффективность резания. Однако проблема энергопотребления не упоминалась. Wu и др. [26] изучали влияние рабочих параметров на результаты и фиксировали движение частиц, но совместимость модели с реальностью требует дальнейшей разработки.
Для достижения лучших рабочих результатов и снижения сопротивления и энергопотребления во время высокоскоростного беспахотного посева в данной статье предлагается комбинированное соломообрабатывающее устройство резания-сгребания. Путем оптимизации профиля лезвия соломорезательного диска и рационализации структуры устройства оптимальная комбинация параметров была определена с помощью дискретно-элементных имитационных испытаний. Эти симуляции использовались для разработки модели взаимодействия соломы и почвы, а оптимальные параметры были впоследствии установлены на сеялку для полевой проверки. Во время высокоскоростной работы устройство эффективно повышает способность очистки от соломы и улучшает показатели посева.
2. Материалы и методы
2.1. Общая структура устройства
В районе Хуан-Хуай-Хай схема возделывания включает две культуры в год с короткими интервалами между послеуборочными работами и посевом. Чтобы максимизировать время роста и повысить эффективность, используются устройства для обработки соломы для удаления соломы с поверхности почвы перед посевом. Однако эти устройства часто приводят к более высокому энергопотреблению, снижению рабочей производительности и недостаточной адаптации к высокоскоростным условиям [6,27,28,29]. Связанные исследования продемонстрировали, что контактирующие с почвой компоненты с большей шириной создают большее сопротивление, что препятствует высокоскоростной работе [30]. Дополнительно, почва и солома приводятся в сложное состояние движения, приводя к плохому коэффициенту удаления соломы (SCR) и несоответствию требованиям посева из-за накопления соломы на очищаемой полосе.
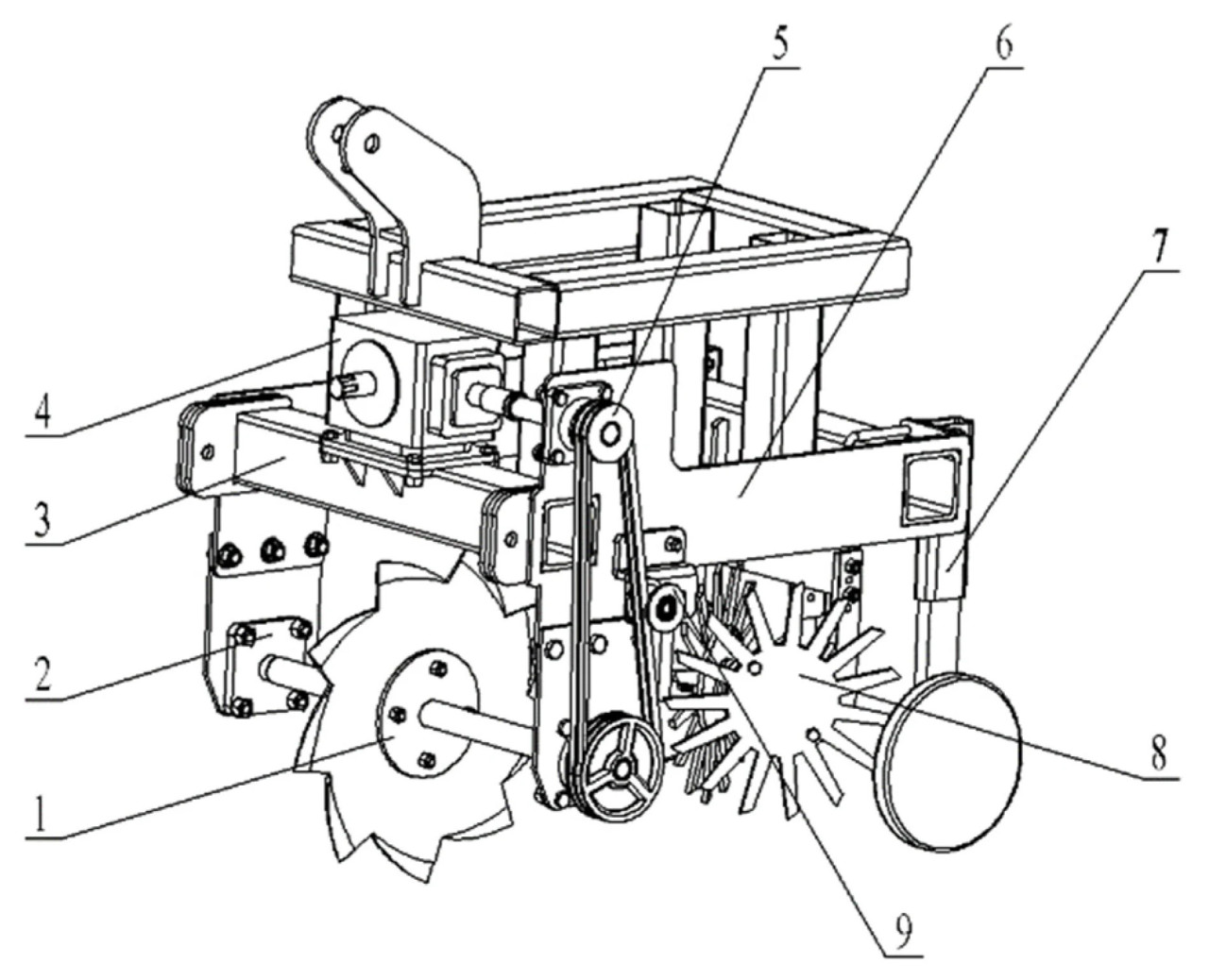
Для решения этих проблем используется режущий элемент меньшей ширины, чтобы снизить риск забивания, когда солома разбросана по полю беспорядочно. Ключевым является проектирование эффективных устройств для обработки соломы. Чтобы обеспечить высококачественную среду семенного ложа для последующих культур и избежать срезания стерни, необходимо тщательно очистить остатки предыдущих культур с полосы посева. Исходя из этих требований, было спроектировано комбинированное устройство для обработки соломы резанием-сгребанием. Это устройство в основном состоит из компонента для резки соломы, компонента для удаления соломы, силового механизма, трансмиссионной системы, механизма ограничения глубины и рамы. Компонент для резки соломы и компонент для удаления соломы расположены спереди и сзади соответственно, их общая структура иллюстрируется на Рисунке 1. Конструкция направлена на повышение эффективности очистки от соломы, снижение энергопотребления и обеспечение оптимальных условий посева при высокоскоростных операциях.
Рисунок 1. Схема комбинированного соломообрабатывающего устройства резания-сгребания. 1. Соломорежущее устройство; 2. корпус подшипника; 3. базовая рама; 4. трансмиссия; 5. приводной узел; 6. боковая пластина; 7. устройство ограничения глубины; 8. устройство для удаления соломы; 9. натяжная шестерня.
2.2. Проектирование ключевых компонентов
Соломорезательный диск непосредственно влияет на операционную эффективность. Чтобы обеспечить эффективное разрезание соломы во время высокоскоростного посева, необходимо оптимизировать кривую режущей кромки соломорезательного диска для поддержания стабильной работы. Используется эвольвентная кривая, определяемая как прямая линия, чисто катящаяся по окружности, чтобы минимизировать относительное скольжение во время процесса резания. Эта конструкция облегчает лучшее взаимодействие между диском, соломой и почвой. Угол скользящего резания должен превышать угол трения между почвой и соломой, или материалом ножа. Обычно угол трения между соломой сельскохозяйственной культуры и металлом составляет от 20° до 40° [31]. Следовательно, оптимальный диапазон резания для угла скользящего резания в начальной и конечной точках проектируемых кривых режущей кромки (Q1, Q2) находится между 50° и 70° [32,33]. Обеспечивая, чтобы угол скользящего резания в каждой точке режущей кромки попадал в этот оптимальный диапазон, и динамически регулируя угол скользящего резания кривой, можно уменьшить длину режущей кромки. Это уменьшение длины режущей кромки, в свою очередь, помогает снизить энергопотребление [34].
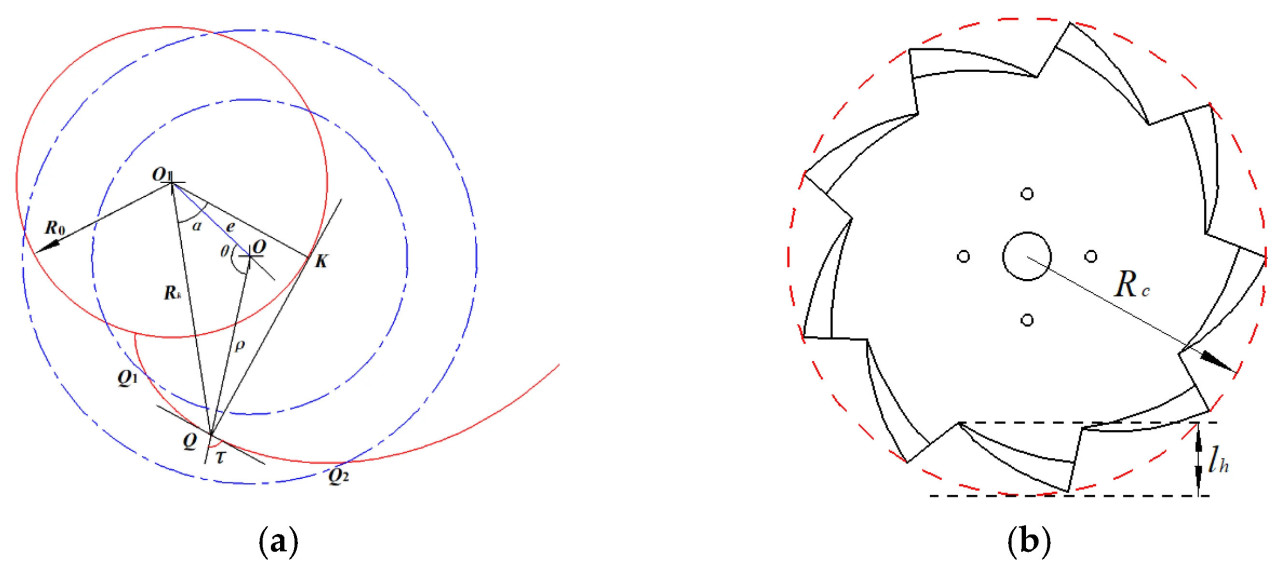
Как иллюстрируется на Рисунке 2а, Q1 и Q2 представляют начальную и конечную точки линии лезвия соответственно. O и O1 обозначают центр вращения и центр основной окружности. R0 – это радиус основной окружности. Рассмотрим точку Q на кривой лезвия, где нормаль к кривой пересекает основную окружность в точке K. Это пересечение определяет угол скольжения в этой точке как τ. Связь между радиус-вектором Rk и R0 задается как R0 = Rk cosα, где loQ = ρ, а эксцентриситет равен e. Это соотношение приводит к следующему выражению для угла скольжения:
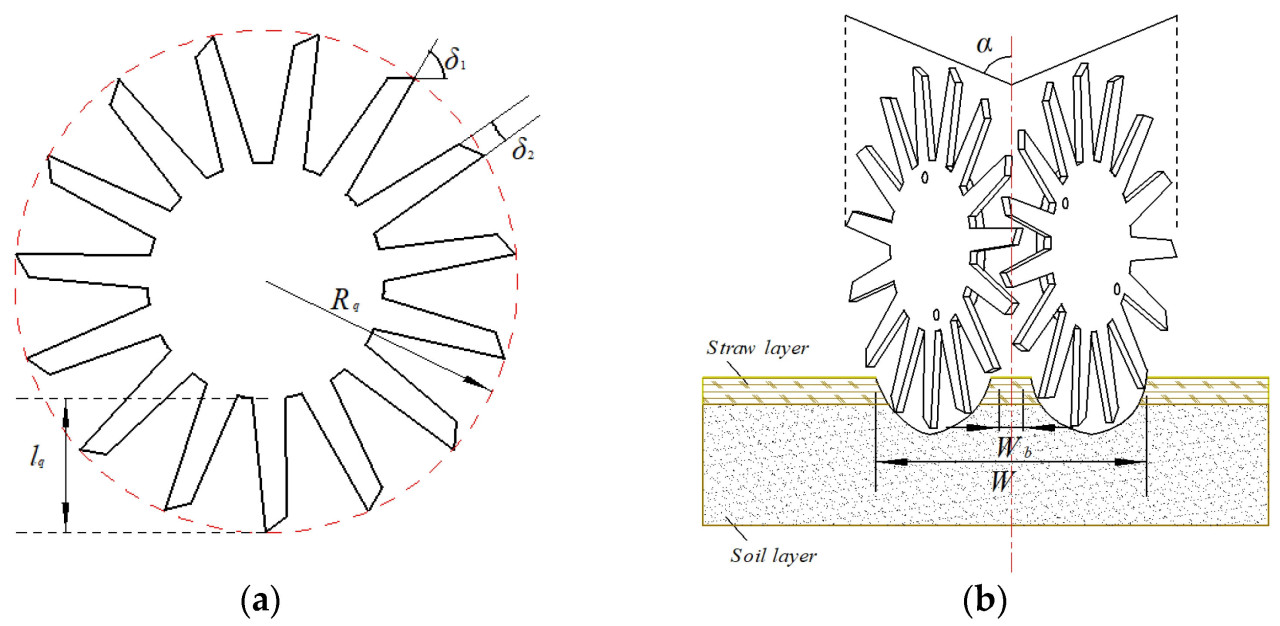
Рисунок 2. Зубчатый дисковый резак. (a) Кривая режущей кромки; (b) Оптимизированный зубчатый диск.
Как показано в уравнении (1), угол скользящего резания τ непрерывно изменяется с положением режущей кромки во время процесса резания, тем самым повышая способность резать солому и рыхлить почву. Выбранная кривая режущей кромки поворачивается против часовой стрелки вокруг центра вращения, в результате чего образуется множество выемок (1-я выемка, 2-я выемка, 3-я выемка, …, 9-я выемка). Чтобы обеспечить твердость и безопасность диска, в качестве материала была выбрана сталь 65Mn, и использовалась эксцентричная кривая для более легкого изготовления. Положения корней зубьев подвержены значительному сопротивляющему напряжению, что может привести к поломке зуба [35]. Дополнительно, когда зазор между зубьями диска минимален, солома может застревать в промежутках, вызывая серьезное забивание. Поэтому необходимо увеличить зазор между зубьями, сохраняя при этом оптимальный диапазон угла скольжения. Чтобы предотвратить забивание соломой у корней зубьев, конструкция включает скругленную кривую у основания каждого зуба, увеличивая зазор внизу. Конструкция соломорезательного диска иллюстрируется на Рисунке 2b.
Глубина посева летней кукурузы обычно составляет 3–5 см, а глубина обработки H установлена на 5,5 см, чтобы минимизировать нарушение почвы. Если зубья слишком длинные, они могут сломаться, снижая плавность работы. Поэтому высота зубьев диска lh установлена на 6 см, чтобы обеспечить стабильность работы. Во время процесса резки соломы может возникнуть забивание из-за наматывания на ось диска, когда вал диска расположен слишком низко. Наоборот, высокий вал диска приводит к чрезмерно большому радиусу вращения, вызывая вращательное забивание и увеличение дисбаланса вращения [10,33,36]. Чтобы соответствовать требованиям высокоскоростной работы и на основе опыта эксплуатации, толщина соломорезательного диска установлена на 6 мм, при толщине лезвия 1,2 мм. Радиус вращения спроектирован как Rc = 245 мм.
Солома является полым, гибким материалом, и ее движение приводит к увеличению столкновений, отскоков и других динамических состояний. Чтобы смягчить влияние этих непредсказуемых движений и достичь оптимальной зоны очистки, используются противоположно установленные пальцевидные соломоочистные диски, которые помогают удалять обратно засыпанную и беспорядочно движущуюся солому. Дополнительно, наклоненные кончики пальцев дисков измельчают крупные комья почвы, снижая сопротивление, возникающее во время работы. Перекидывающее действие соломоочистного диска перемещает солому из зоны посева, эффективно предотвращая помехи и накопление соломы. Уменьшение расстояния на вершине очистных зубьев минимизирует площадь просыпания соломы (Wb), обеспечивая чистоту полосы посева. Схематическая диаграмма зоны очистки показана на Рисунке 3. В районе Хуан-Хуай-Хай обычно используются как рядовой посев, так и посев широкой лентой. Рядовой посев располагает семена равномерно распределенными рядами с междурядьем 15 см, оставляя 30-сантиметровую полосу посева кукурузы, в то время как посев широкой лентой использует междурядье 20 см без резервирования полосы посева кукурузы. Было показано, что посев широкой лентой повышает урожайность пшеницы [37]. Чтобы достичь оптимальных показателей посева и снизить рабочее сопротивление, рабочая зона между рядами была спроектирована так, чтобы избегать срезания стерни. Соответственно, максимальная ширина рабочей зоны была установлена на 20 см, угол установки соломоочистного диска установлен на 28°, а рабочая глубина на 2 см. Радиус вращения соломоочистного диска был рассчитан как 170 мм. Чтобы предотвратить подбор соломы и ее сползание к корням во время процесса сброса, вершины зубьев для сгребания соломы были спроектированы с наклонным профилем, чтобы направлять солому наружу, обеспечивая эффективность полосы посева. Эта конструкция помогает сохранять очищающий эффект полосы посева и снижает частоту забивания. На основе опыта эксплуатации и комплексного анализа значения для δ1 и δ2 были установлены на 58° и 3,5° соответственно, чтобы обеспечить равномерную очистку соломы и оптимальную ширину рабочей зоны W:
где α - угол между соломоочистным диском и направлением движения (°), L - расстояние между точкой пересечения соломоочистного диска с поверхностью земли (см), а Wb - площадь просыпания соломы (см).
Рисунок 3. Соломоочистной диск. (a) Структура соломоочистного диска; (b) схема встречной установки.
2.3. Анализ рабочего процесса
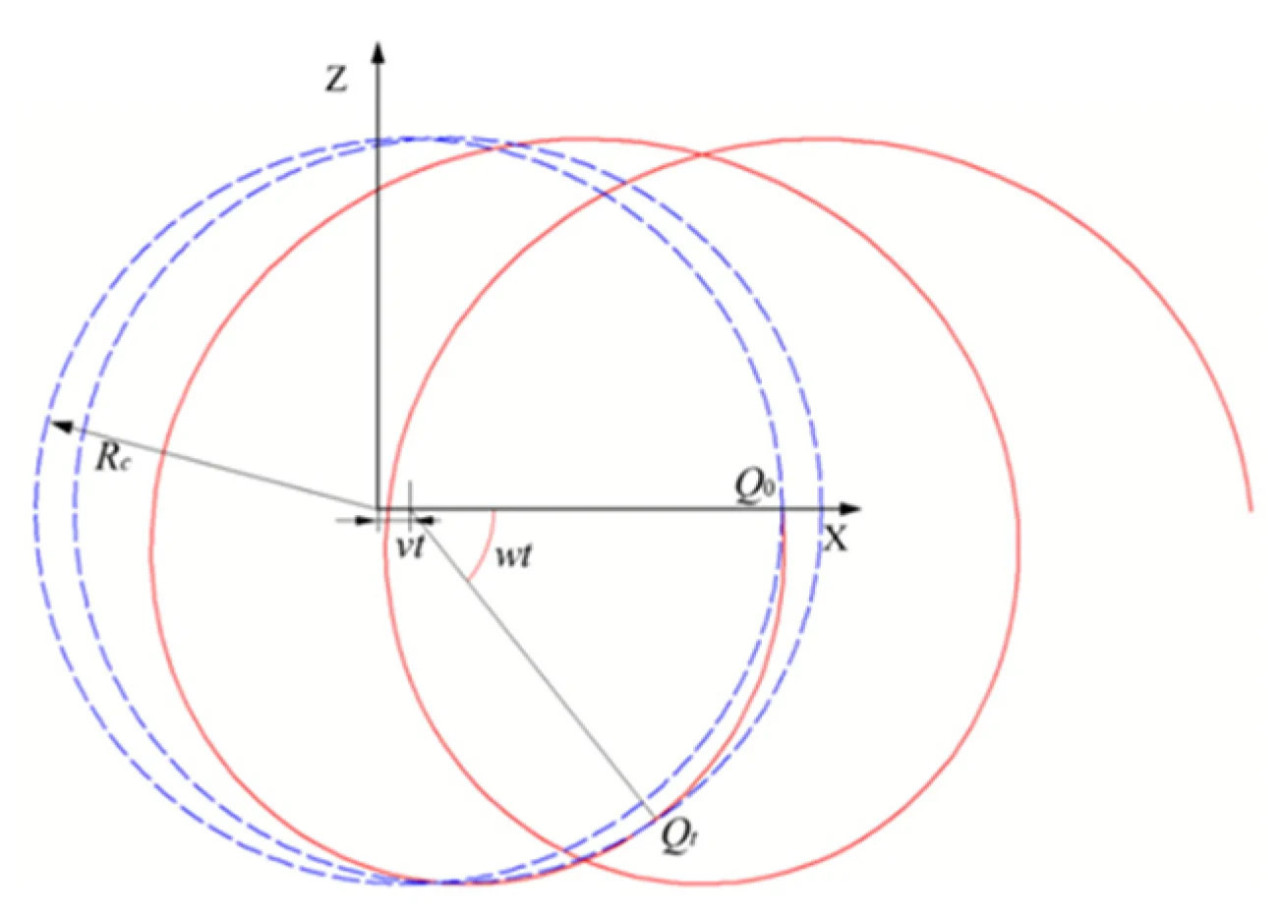
Во время работы орган не только совершает круговое движение вокруг оси ножа, но и движется с постоянной скоростью под тягой трактора. Рабочая скорость обозначается как Vi. Оптимальная производительность резки соломы достигается, когда траектория вершины диска Q пересекается с трохоидой, как показано на Рисунке 4.
Рисунок 4. Траектория конечной точки диска Q.
Его уравнение движения показано в уравнении (3):
где XM и ZM - смещение точки M вдоль осей x и z (м) соответственно. Rc - радиус вращения соломорезательного диска (м), w - угловая скорость вращения соломорезательного диска (рад/с), а t - время работы (с). Из Рисунка 4 видно, что точка Q находится в Q0 при t = 0. Дифференцируя уравнение (3), абсолютная скорость движения точки Q задается уравнением (4):
Как указано уравнением (4), и рабочая скорость, и скорость вращения являются ключевыми факторами, влияющими на рабочие показатели, когда радиус Rc определен. Во время высокоскоростной работы разница между мгновенной линейной скоростью в точке контакта диска с почвой и рабочей скоростью минимальна, когда соломорезательный диск вращается вперед с низкой скоростью вращения, что снижает эффективность непрерывного резания соломы и увеличивает вероятность неэффективности работы. Наоборот, увеличение скорости вращения приводит к более высокому энергопотреблению. Чтобы оптимизировать производительность, для соломорезательного диска принята схема обратного вращения. Этот подход увеличивает относительную скорость между диском и землей, облегчая более эффективное режущее действие, при котором солома подается вперед и разделяется по обе стороны от очищаемой полосы.
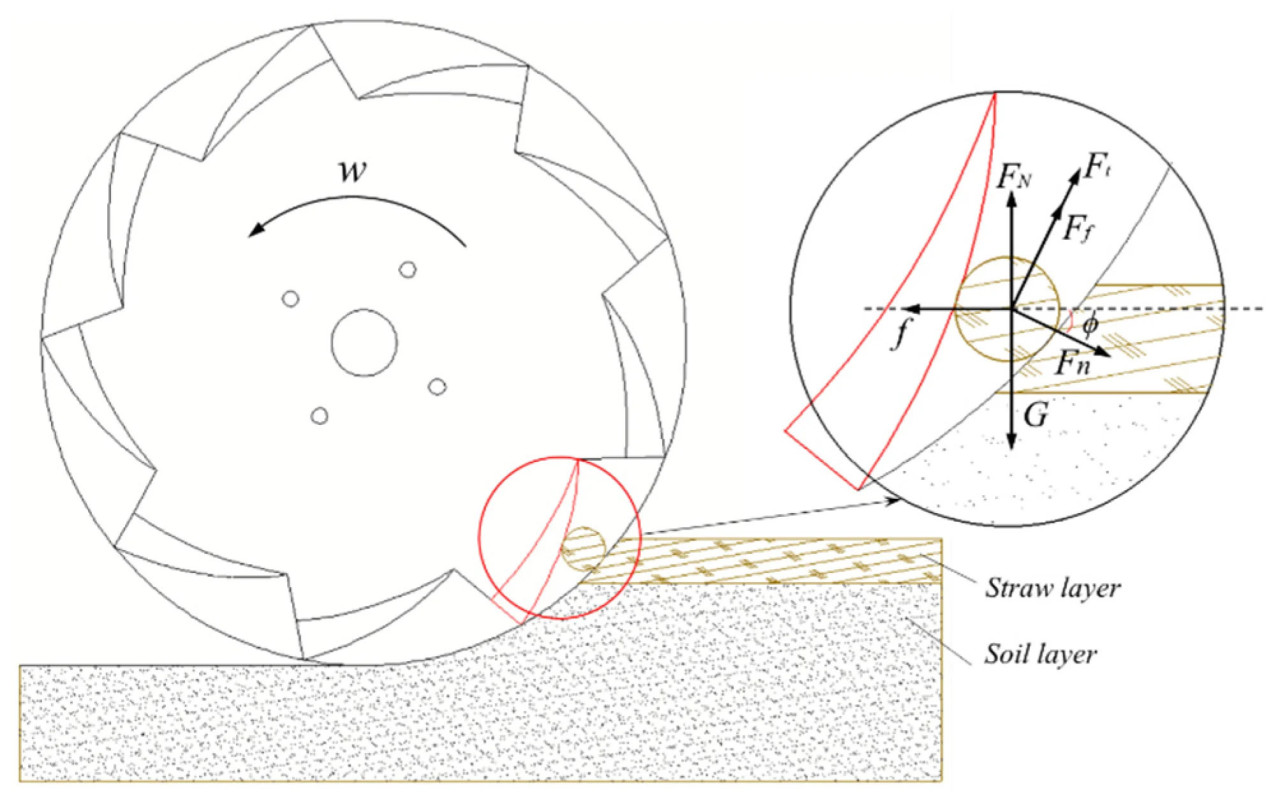
Предполагается, что диск последовательно режет определенную область соломы. Процесс резания анализируется путем изучения сил, действующих на солому, как показано на Рисунке 5. Режущая кромка диска в критической точке входит в контакт с соломой при достижении критического состояния резания. С этого момента соломорезательный диск скользит относительно соломы, заставляя солому перемещаться от проксимального к дистальному концу лезвия и разрезаться.
Рисунок 5. Анализ сил процесса резки соломы.
Пренебрегая сопротивлением воздуха и эффектами взаимных столкновений между сегментами соломы и предполагая сбалансированное условие резания, следующее дифференциальное уравнение движения выводится путем исследования сил, действующих на солому:
где Ff1 - сила трения между соломорезательным диском и соломой (Н), Ft1 - тангенциальная сила между соломорезательным диском и соломой (Н), Fn1 - нормальное давление, оказываемое соломорезательным диском на солому (Н), FN1 - сила, оказываемая почвой на солому (Н), G1 - сила тяжести соломы (Н), f1 - сила трения между соломой и почвой (Н), ϕ - угол между направлением движения и нормалью к режущей кромке зубьев (°), xn и xt представляют смещение соломы в нормальном и тангенциальном направлениях линии лезвия (м) соответственно. Анализ показал, что область накопления соломы открывается, когда солома контактирует с режущей кромкой и скользит к дистальному концу, что приводит к выталкиванию соломы с обеих сторон и разрезанию центральной части. Уравнение (5) демонстрирует, что солома поднимается из почвенных ограничений, вызывая увеличение ее ускорения в нормальном направлении, в то время как в тангенциальном направлении оно уменьшается по мере увеличения угла ϕ. Следовательно, солома продвигается вперед в нормальном направлении режущей кромки, предотвращая ее падение обратно на очищаемую полосу. Это действие снижает риск вторичного резания и минимизирует энергопотребление. Дополнительно, это сокращает путь резания и повышает эффективность резания благодаря катящемуся движению, тем самым улучшая рабочие показатели и снижая риск забивания. Однако более высокие скорости вращения заставляют солому отбрасываться ближе к режущей кромке, продлевая время контакта и увеличивая энергопотребление. Наоборот, более низкие скорости вращения приводят к тому, что солома отбрасывается дальше от режущей кромки, сокращая время контакта и приводя к недостаточному резанию. Таким образом, эффективность режущей кромки ограничена скоростью вращения.
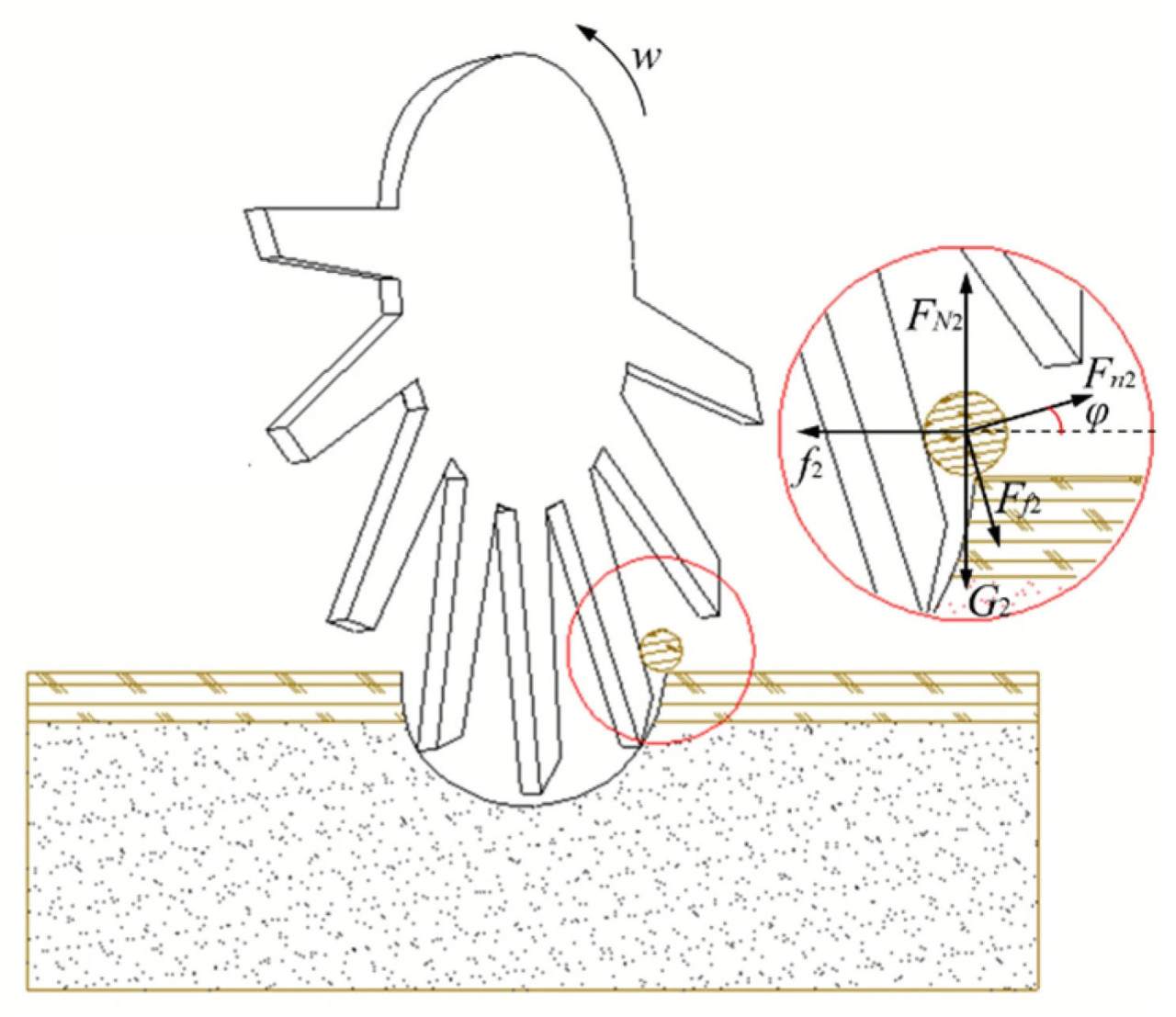
Во время процесса удаления соломы зубья соломоочистного диска проникают в слой соломы, генерируя вращательное движение при контакте. Линейная скорость кончиков зубьев соответствует рабочей скорости. В непрерывном движении соломы необходимо преодолеть трение о землю и трение между зубьями ножа и соломой, что приводит к выталкиванию соломы. Рисунок 6 иллюстрирует силу, действующую на солому, и соотношение выражается уравнением (6):
где f2 представляет трение между соломой и почвой (Н), Ff2 - трение между соломой и очистным диском (Н), G2 - сила тяжести (Н), Fn2 - усилие толкания очистных зубьев на солому (Н), FN2 - сила, оказываемая почвой на солому (Н), φ - угол между нормальным направлением контактной поверхности очистных зубьев и горизонтальным направлением (°).
Рисунок 6. Анализ процесса очистки соломы.
Угол φ постепенно увеличивается от точки, где зубья контактируют с соломой, до точки, где они отходят от нее. Тангенциальное ускорение увеличивается быстрее, чем нормальное ускорение, заставляя траекторию соломы смещаться в сторону очистных зубьев. Когда скорость соломы ниже линейной скорости очистных зубьев в точке контакта, солома движется вместе с очистными зубьями. Из-за характеристик очистных зубьев солома скользит наружу, снижая риск забивания. Когда солома достигает вершины очистных зубьев, она отделяется от зубьев, демонстрируя наклонную нисходящую траекторию, когда ее скорость превышает линейную скорость в точке отрыва. Наоборот, когда скорость соломы меньше линейной скорости в точке отрыва, она остается близко к очистным зубьям и выталкивается наружу пандусом на вершине, чтобы предотвратить вращение. Очевидно, что рабочая скорость оказывает значительное влияние на эффективность обработки соломы, как упомянуто выше.
После обработки соломы соломорезательным диском она постепенно отделяется от диска, становясь самостоятельным движущимся телом и возвращаясь в статическое состояние, в то время как соломоочистной диск продолжает работать. Установка меньшего расстояния между двумя компонентами увеличивает сложность движения почвы и соломы в зоне обработки, тем самым снижая успешность обработки соломы. Наоборот, установка большего расстояния увеличивает общую продольную длину машины, напрямую влияя на ее стабильность. Поэтому монтажное расстояние между двумя компонентами играет ключевую роль в общей эффективности работы.
2.4. Построение модели дискретно-элементного моделирования
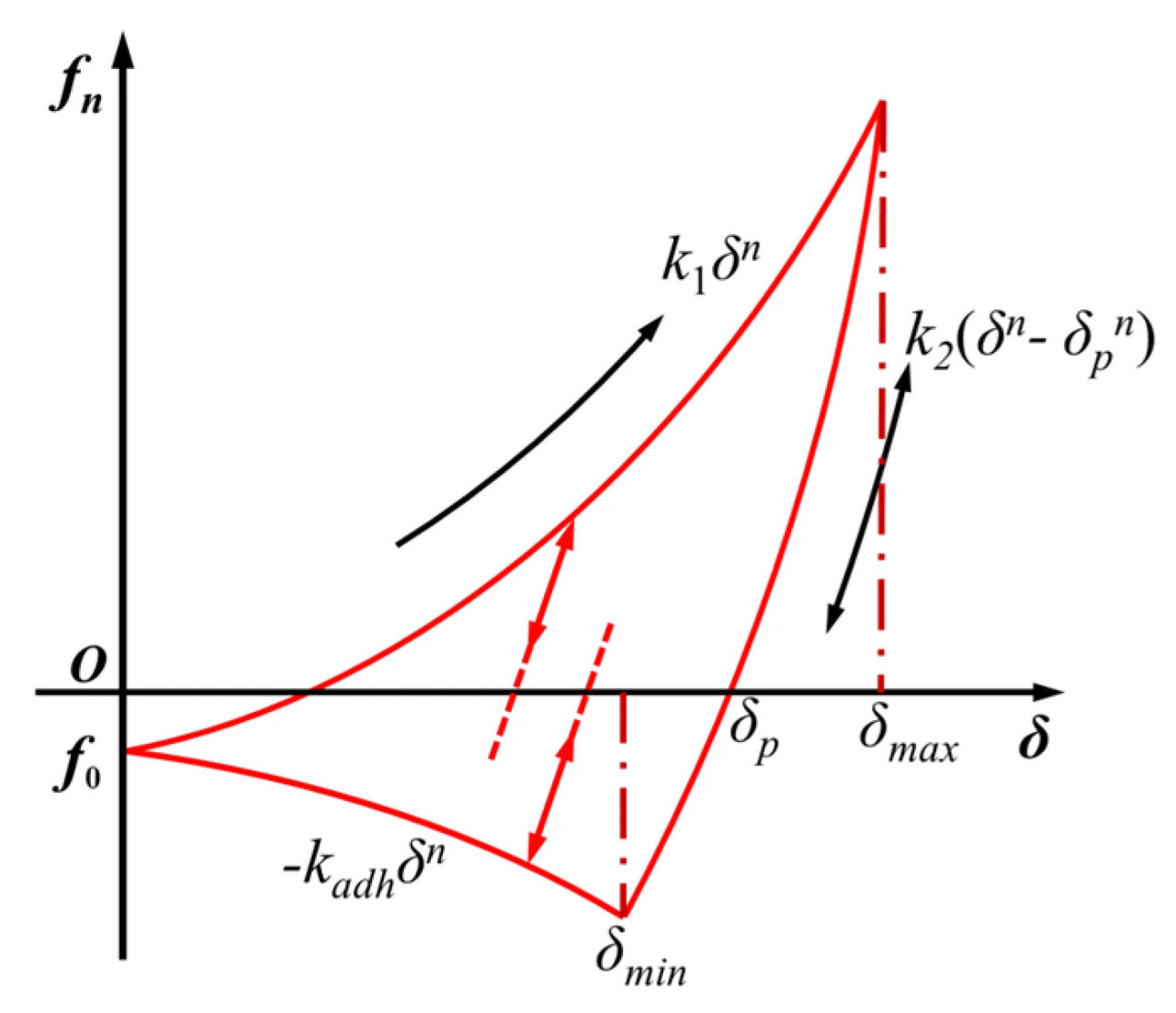
В условиях беспахотного посева почва уплотняется, что приводит к изменению ее механических свойств по сравнению с исходным состоянием. Чтобы точно смоделировать эти характеристики, была выбрана модель эластопластического сцепления Эдинбурга (EEPA), которая включает вязкое, упругое и пластическое поведение [38,39]. Связь между нормальной контактной силой и смещением для этой контактной модели показана на Рисунке 7.
Рисунок 7. Зависимость нормальной контактной силы от смещения для контактной модели.
Полная нормальная контактная сила fn в основном состоит из силы гистерезисного восстановления fhys и нормальной демпфирующей силы fnd. Соотношение перекрытия между нормальной контактной силой и межчастичным для этой модели контакта частиц подробно описано в уравнениях (7)–(9):
где u представляет единичный вектор нормали, направленный от точки контакта к центру масс, f0 обозначает начальную прочность связи между частицами (Па). k1 и k2 соответствуют коэффициентам жесткости при нагрузке и разгрузке соответственно, в то время как δp указывает расстояние перекрытия в точке контакта между частицами (мм), kadh отражает коэффициент прочности вязкого сцепления. vn - нормальная контактная скорость (м/с). βn представляет коэффициент демпфирования. m обозначает эффективную массу контактирующих частиц, а e - коэффициент восстановления почвенных частиц.
Тангенциальная контактная сила между частицами (ft) в модели почвы состоит из тангенциальной жесткости (fts) и тангенциального демпфирования (ftd). Их соотношение выражается уравнением (10):
Тангенциальная жесткость между частицами определяется итеративно, как представлено в уравнении (11):
где fts(n−1) представляют тангенциальную силу в момент времени (Н), а Δ - шаг по времени (с). Δfts обозначает приращение тангенциальной силы (Н), в то время как γt - коэффициент тангенциальной жесткости частиц. δt представляет тангенциальное перекрытие между частицами (мм). Тангенциальное демпфирование в основном зависит от межчастичного коэффициента тангенциального демпфирования βt и межчастичной тангенциальной скорости vt, как описано следующим уравнением (12):
Почвенные частицы испытывают взаимодействия скольжения, с тангенциальным трением, управляемым критерием трения Кулона. Соответственно, прочность на сдвиг частицы при нормальном напряжении ограничена следующим образом:
где fct обозначает максимальное тангенциальное трение между частицами (Н), а μ - коэффициент статического трения между частицами.
В EDEM размеры почвенных частиц были определены на основе результатов ситового анализа. Чтобы снизить вычислительную нагрузку, частицы крупнее 4 мм были установлены на 5 мм, что составляет 35,46% от общего числа, в то время как частицы меньше 4 мм были установлены на 3 мм, составляя 64,54% [39,40]. Модель контакта EEPA состояла из девяти параметров: коэффициент восстановления при столкновении, коэффициент статического трения, коэффициент динамического трения, постоянная сила отрыва, поверхностная энергия, пластическая деформация контакта, индекс ветви нагрузки, индекс ветви сцепления и коэффициент тангенциальной жесткости. Поскольку постоянная сила отрыва остается между частицами, она была исключена из этого исследования. Индекс ветви нагрузки в программном обеспечении EDEM 2022 был ограничен значениями между 1 и 1,5, со значением 1,5, выбранным на основе существующей литературы [41].
После предварительной калибровки и проверочных испытаний для обеспечения пригодности для высокоскоростной работы согласно литературе [40], параметры для контактной модели почвы были определены, как показано в Таблице 1, и сгенерированная модель почвы представлена на Рисунке 8.
Рисунок 8. Модель почвы.
Таблица 1. Параметры моделирования контакта почвы.
Пшеничная солома случайным образом распределена в поле и проявляет гибкость, генерируя сложный процесс движения во время работы оборудования. Чтобы точно представить исходную солому, была разработана модель полой гибкой соломы с использованием модели Hertz–Mindlin Bonding V2 в EDEM, где сцепление устанавливалось между частицами для моделирования эффектов растяжения, сжатия, сдвига и кручения [42,43]. Пользовательские свойства, включая силу (Fn,t) и момент (Mn,t), определяются следующим образом:
где dFn, dFt, dMn и dMt представляют приращения нормальной силы (Fn), силы сдвига (Ft), крутящего момента (Mn) и изгибающего момента (Mt) соответственно. dδn, dδt, dθn и dθt являются приращениями нормальной деформации (δn), деформации сдвига (δt), угловой деформации кручения (θn) и угловой деформации изгиба (θt). Kn, Kt, Kmn и Kmt представляют нормальную, сдвиговую, крутильную и изгибную жесткости соответственно. Связь моделируется как цилиндр с радиусом RB, длиной lb, площадью поперечного сечения A = πrb2, моментом инерции площади I = πRB4/4 и полярным моментом инерции площади Ip = πRB4/2. Eb и Gb представляют модуль Юнга и модуль сдвига соответственно. Деформация связи рассчитывается на основе соответствующих скоростей (vn, vt, wn, wt) и произведения шага по времени (dt).
Движение сферических частиц и всех компонентов частиц управляется вторым законом Ньютона:
где x и θ представляют поступательное смещение и угловое смещение сферических частиц с массой (m) и моментом инерции вращения (J) соответственно, F обозначает результирующие силы, приводящие к поступательному движению компонентов соломы (Н), а M представляет результирующие силы, приводящие к их вращательному движению (Н·м).
Разрыв связи происходит, когда нормальные и тангенциальные напряжения сдвига превышают пороговые значения, определенные для растрескивания соломы, как показано в уравнении (16):
где σmax - максимальное положительное напряжение, а τ - максимальное напряжение сдвига.
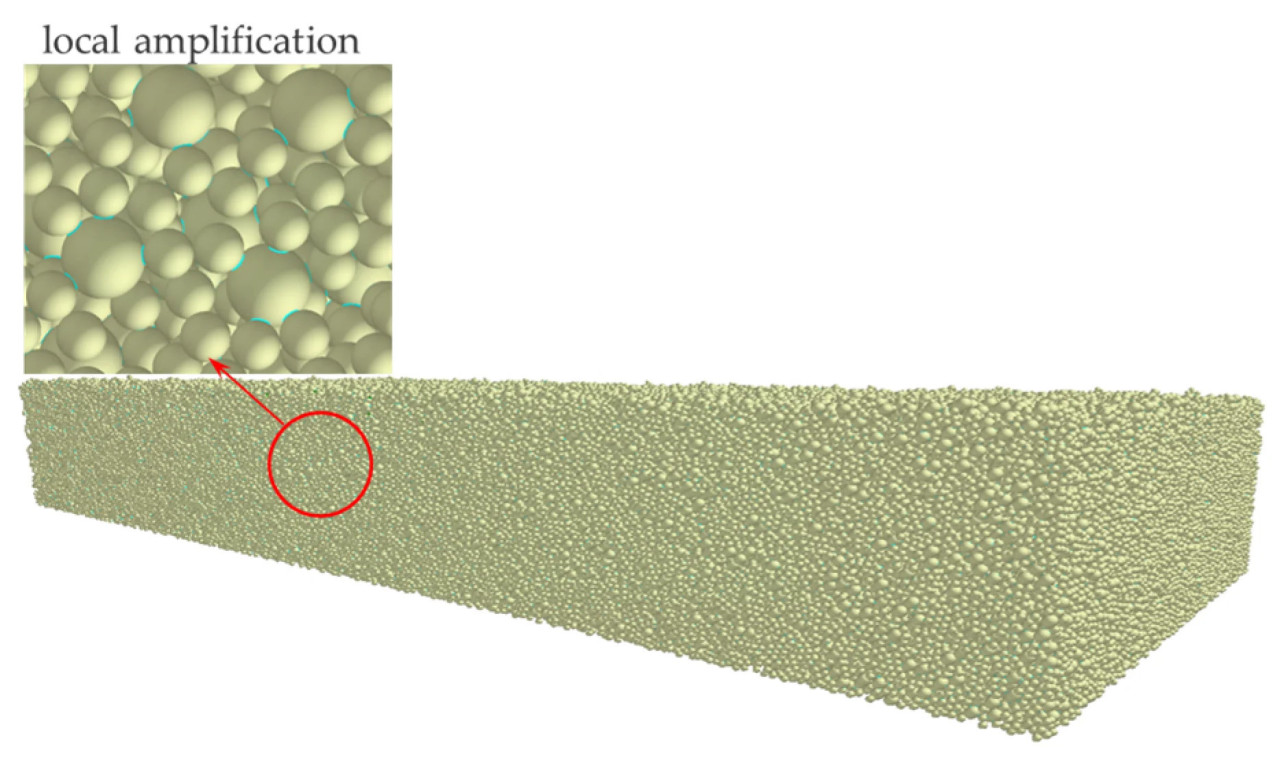
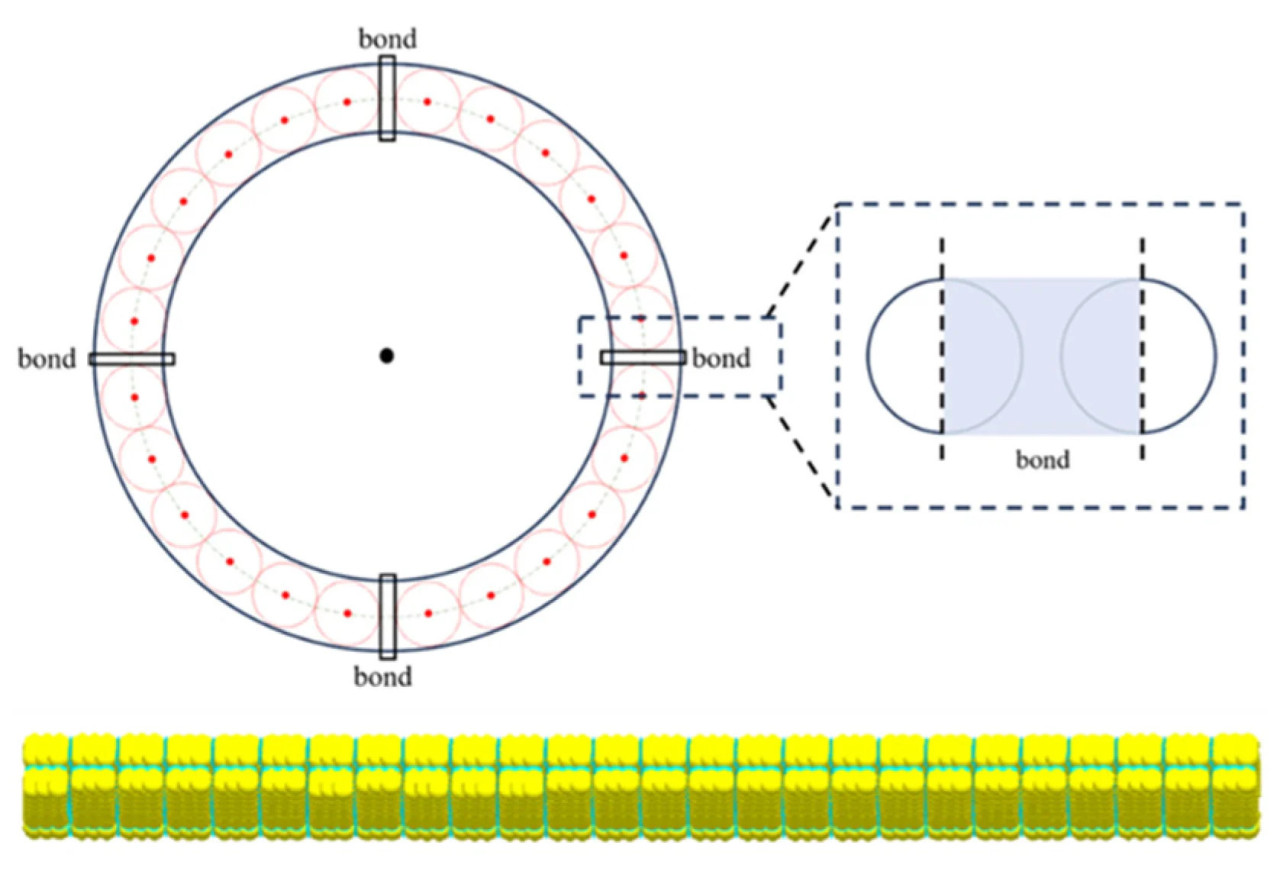
Согласно требованиям беспахотного посева для района Хуан-Хуай-Хай, пшеничная солома измельчается на длины менее 10 см и равномерно распределяется по поверхности почвы. Полевые собранные образцы показали, что длины соломы варьировались от 3 см до 9 см. Чтобы упростить построение модели и снизить вычислительные потребности, средняя длина 6 см была выбрана в качестве стандартной длины для модели соломы. Модель Hertz–Mindlin Bonding V2 была использована для разработки дискретно-элементной модели в программном обеспечении EDEM 2022. Параметры для этой модели соломы — включая нормальную жесткость на единицу площади, жесткость сдвига на единицу площади, нормальную прочность, прочность на сдвиг и масштаб диска связи (установленный на 1) — были откалиброваны с помощью экспериментальных испытаний, как перечислено в Таблице 2.
Таблица 2. Параметры контактной модели соломы.
Согласно методологии, описанной в [32], дискретно-элементная модель соломы — основанная на вышеупомянутых параметрах — иллюстрируется на Рисунке 9.
Рисунок 9. Модель соломы.
2.5. Методы испытаний
Чтобы оптимизировать время моделирования и снизить сложность, модель устройства была упрощена с сохранением основных функций соломорезательного диска и соломоочистного диска. Модель взаимодействия, включающая компоненты устройства, солому и почву, была разработана с использованием программного обеспечения EDEM 2022. Соломорезательный диск был смоделирован с использованием материала 65Mn, характеризующегося коэффициентом Пуассона 0,30, плотностью 7800 кг/м3 и модулем упругости 2,054 × 10¹¹ Па. Параметры пшеничной соломы были установлены с коэффициентом Пуассона 0,40, плотностью 241 кг/м3 и модулем упругости 5,141 × 10⁸ Па, в то время как параметры почвы были определены с коэффициентом Пуассона 0,38, плотностью 1251 кг/м3 и модулем упругости 1,3 × 10⁶ Па [25,40,41,42]. Дополнительно, был создан почвенный лоток размером 1000 × 300 × 150 мм в качестве ложа частиц.
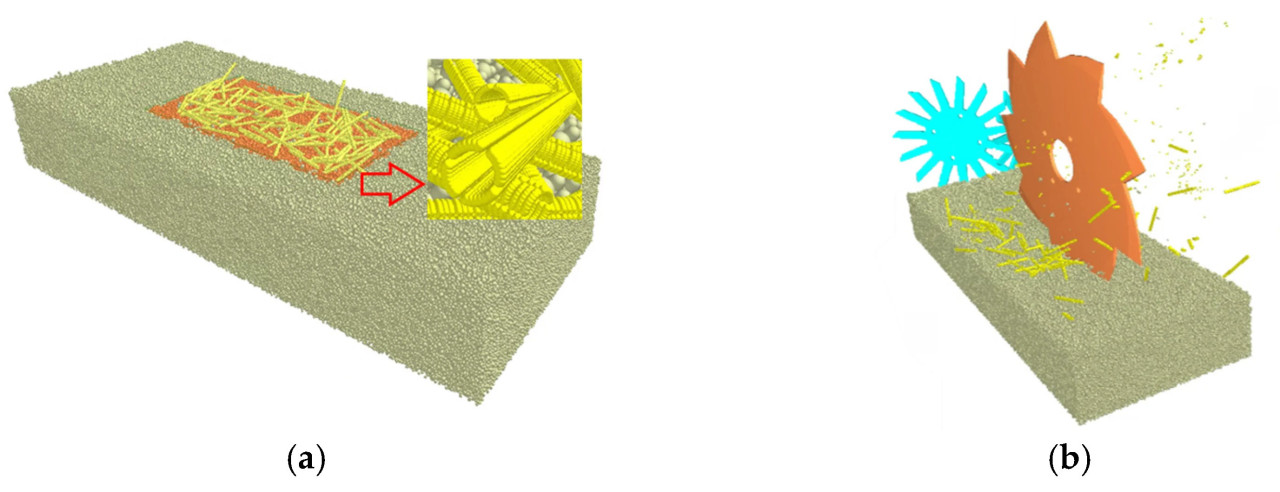
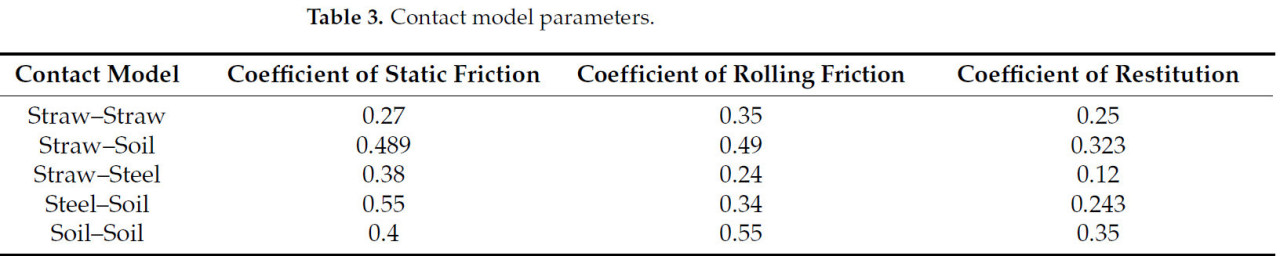
Полая гибкая солома близко имитирует фактическую форму соломы. Однако генерация большого количества соломин для точного представления полевых условий может резко увеличить вычислительные потребности. Чтобы решить эту проблему, соломинки были случайным образом сгенерированы в ограниченной области и распределены над слоем почвы, чтобы соответствовать покрытию соломой, наблюдаемому в поле. Этот подход моделирует естественное рассеяние соломы в посевном поле через динамику свободного падения, тем самым упрощая вычисления. Ширина зоны соответствует ширине ряда посева пшеницы, что меньше выбранной длины зоны. В Таблице 3 приведены параметры для контактных моделей, и модель иллюстрируется на Рисунке 10.
Рисунок 10. Модель дискретно-элементного моделирования. (a) модель почвы и соломы; (b) модель взаимодействия.
Таблица 3. Параметры контактной модели.
DEM предоставляет метод для регулировки рабочих параметров и минимизирует необходимость в обширных полевых испытаниях, тем самым повышая как эффективность, так и точность. Чтобы соответствовать требованиям высокоскоростного посева, были выбраны три уровня рабочей скорости (12, 13 и 14 км/ч). Дополнительно, три скорости вращения соломорезательного диска — конкретно 200, 300 и 400 об/мин (20,94, 31,42 и 41,89 рад/с) — были выбраны для соответствия высокоскоростным условиям. Межосевые расстояния установки 60, 80 и 100 см были установлены на основе практического сельскохозяйственного опыта. Закодированные уровни этих тестовых факторов представлены в Таблице 4.
Таблица 4. Таблица кодов испытаний.
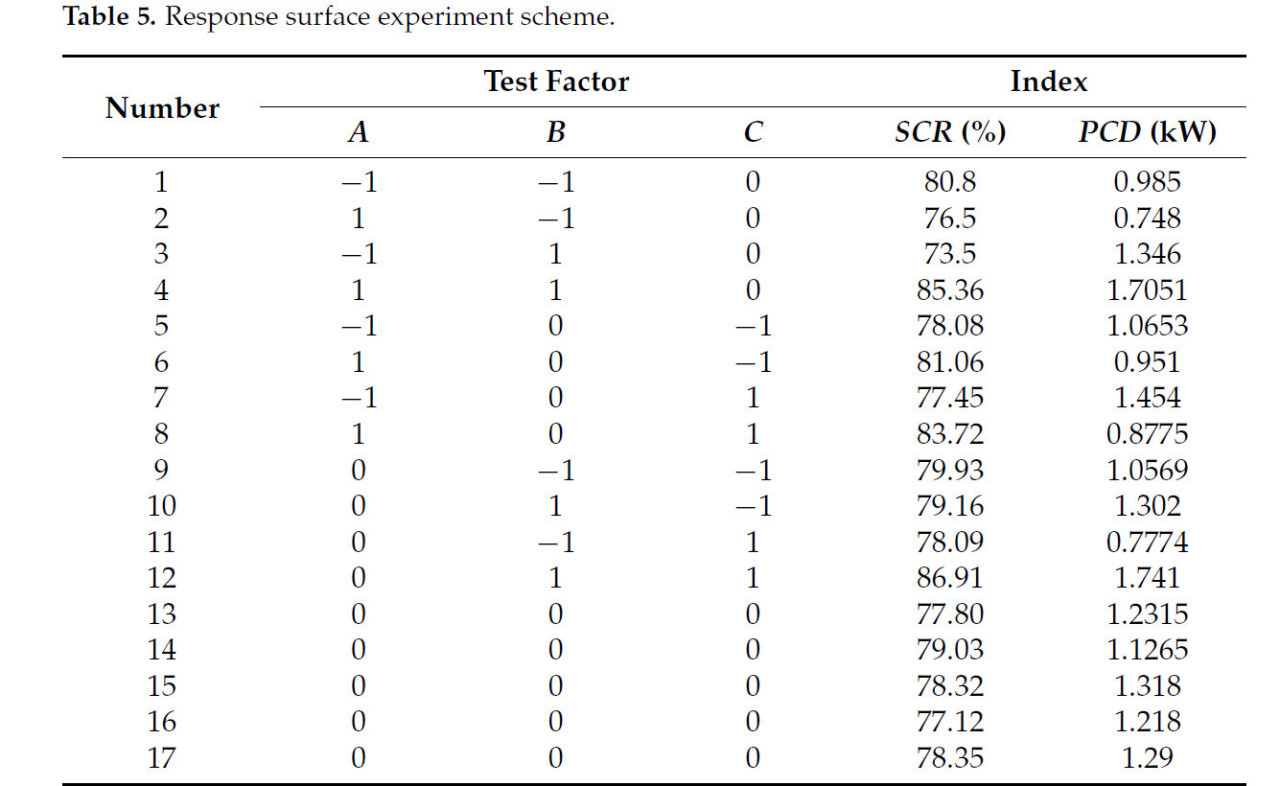
Испытания методом поверхности отклика были проведены на рабочих параметрах с использованием программного обеспечения Design-Expert 12, состоящие из 17 тестовых групп. Модель устройства в формате «igs» была импортирована в программное обеспечение EDEM 2022, где рабочие параметры для компонентов обработки соломы были настроены, как изложено в Таблице 5. Дополнительно, вращение соломоочистного диска было установлено на активное вращение, заменяя пассивное вращение, чтобы обеспечить совместимость с рабочей скоростью. На основе анализа процесса работы испытания методом поверхности отклика были выполнены с использованием коэффициента удаления соломы (SCR) и энергопотребления соломорезательного диска в качестве оценочных метрик. SCR рассчитывался с использованием уравнения (17):
где m1 представляет вес оставшейся соломы (кг), а m0 обозначает начальный вес соломы (кг).
Таблица 5. Схема эксперимента с поверхностью отклика.
Крутящий момент, действующий на соломорезательный диск при контакте с частицами во время процесса моделирования, измерялся, и энергопотребление соломорезательного диска (PCD) рассчитывалось с использованием уравнения (18):
где T - крутящий момент соломорезательного диска (Н·м), а n - скорость вращения соломорезательного диска (об/мин).
3. Результаты и обсуждение
3.1. Анализ результатов
3.1.1. Дисперсионный анализ
Экспериментальный план и результаты представлены в Таблице 5, где факторы A, B и C соответствуют рабочей скорости, скорости вращения и межосевому расстоянию установки соответственно. Дисперсионный анализ (ANOVA) был проведен на результатах моделирования для оценки статистической значимости (p < 0,05).
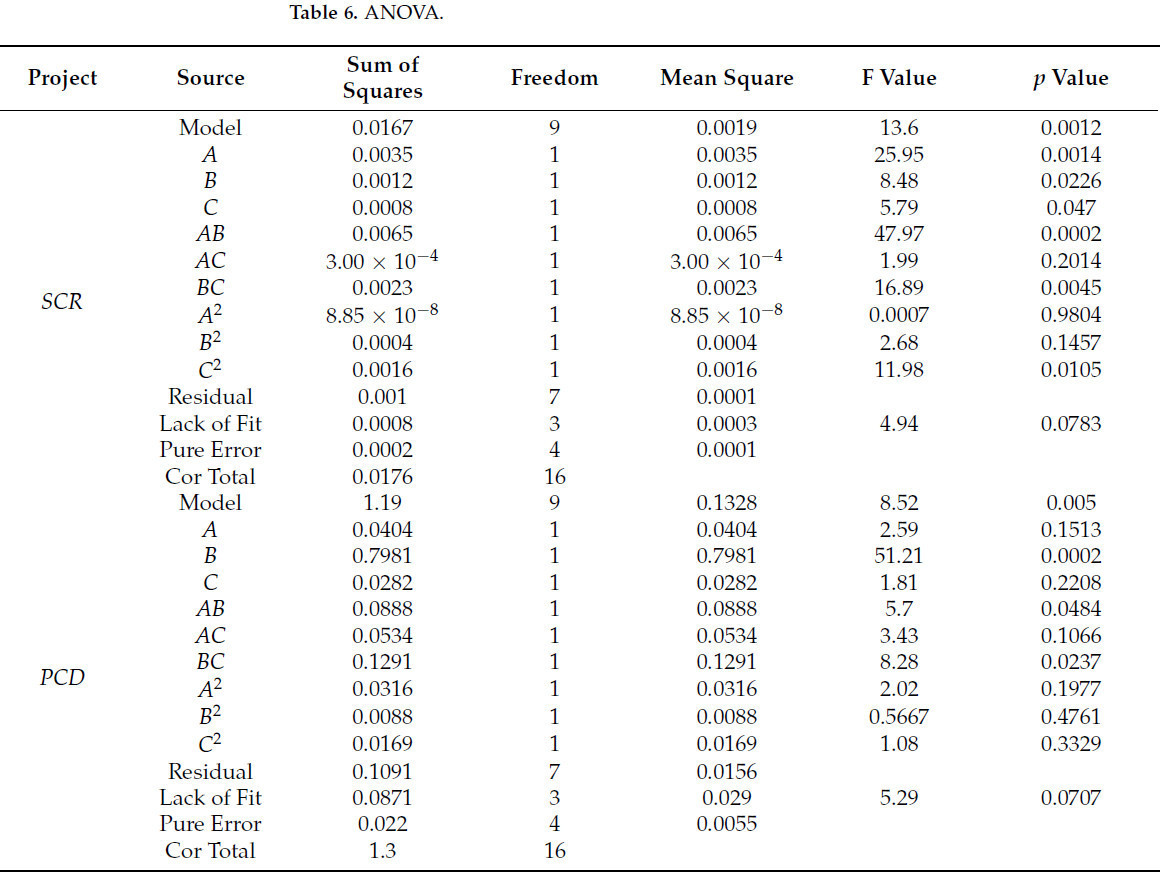
Результаты ANOVA для SCR представлены в Таблице 6, демонстрируя общий значительный эффект (p < 0,01). Рабочая скорость, скорость вращения и межосевое расстояние установки каждый оказывают значительное влияние на SCR. Дополнительно, эффекты взаимодействия AB и BC, а также квадратичный член C2 являются значимыми. Другие члены взаимодействия и квадратичные члены не оказывают значительного влияния на значения отклика. Факторы, влияющие на SCR, ранжированы в порядке важности следующим образом: A > B > C. После удаления незначимых факторов регрессионное уравнение, описывающее влияние каждого фактора на коэффициент удаления соломы, показано в уравнении (19):
Таблица 6. ANOVA.
Был проведен тест на отсутствие соответствия по дисперсии, выявивший незначимость (p > 0,05). Это указывает, что результаты испытаний надежны и что регрессионное уравнение обеспечивает отличное соответствие. Коэффициент детерминации (R2) равен 0,9459, который снижается до 0,9098 после удаления незначимых факторов. Это предполагает, что модель учитывает более 90% дисперсии в результатах, делая ее пригодной для прогностических целей.
ANOVA для PCD представлен в Таблице 6, с общими экспериментальными результатами, являющимися значимыми (p < 0,01). Эффект скорости вращения на PCD был весьма значительным. Дополнительно, эффекты взаимодействия факторов AB и BC на энергопотребление были значимыми, в то время как оставшиеся члены не были. Порядок влияния на значение отклика следующий: B > A > C. После исключения незначимых факторов регрессионное уравнение, описывающее влияние каждого уровня фактора на PCD, предоставлено в уравнении (20):
Тест на отсутствие соответствия был проведен на дисперсии и оказался незначимым (p > 0,05), указывая, что результаты испытаний надежны и что регрессионное уравнение обеспечивает отличное соответствие. Коэффициент детерминации (R2) равен 0,9163. После удаления незначимых факторов R2 снижается до 0,8317, что предполагает, что модель объясняет более 83% дисперсии в результатах, делая ее пригодной для прогностических целей.
3.1.2. Анализ поверхности отклика
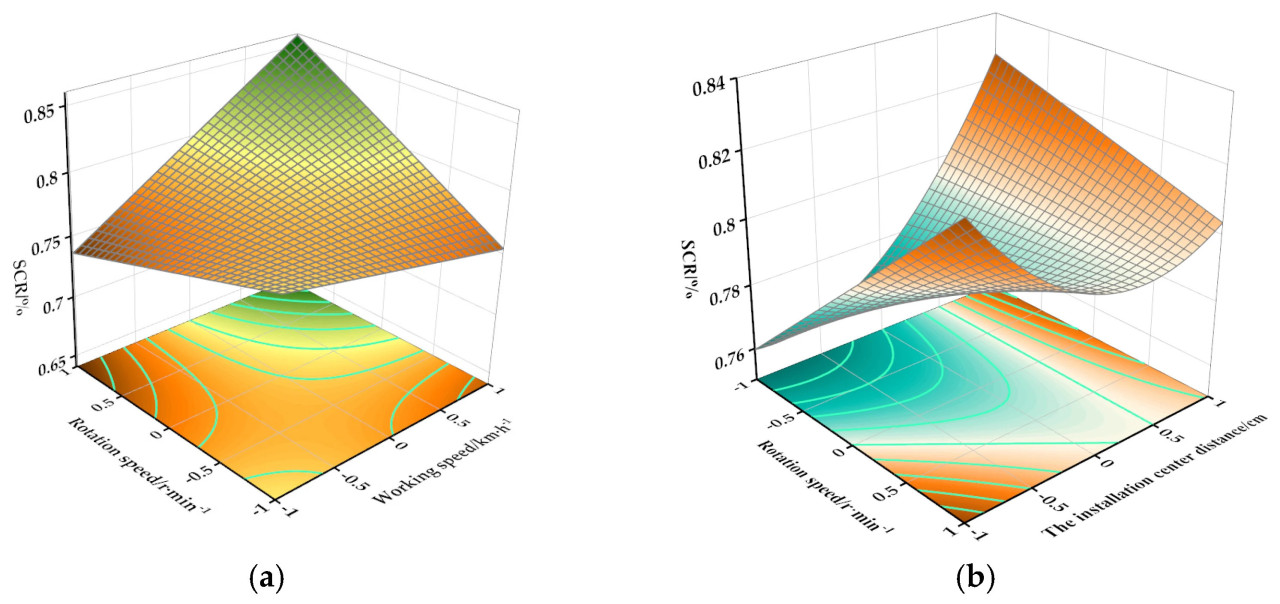
Чтобы исследовать эффекты взаимодействий факторов на экспериментальные показатели, результаты были проанализированы с использованием методологии поверхности отклика в программном обеспечении Design-Expert 12, как иллюстрируется на Рисунках 11 и 12.
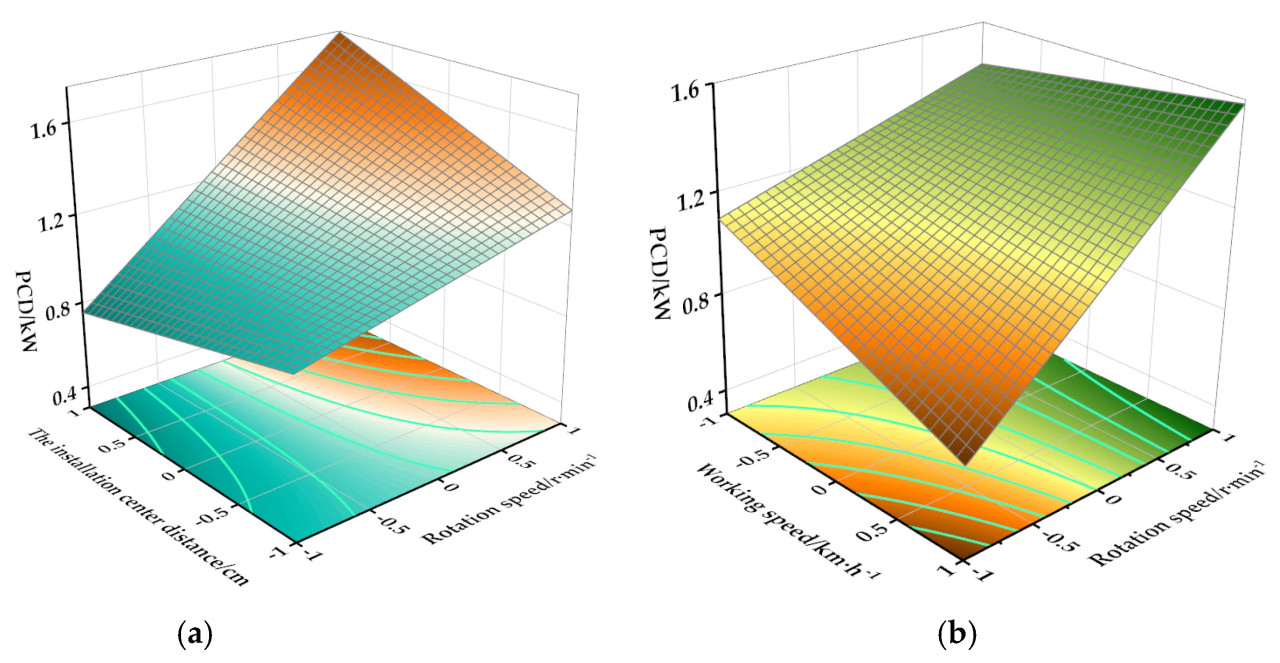
Рисунок 12. Поверхность отклика взаимодействующих факторов, влияющих на PCD. (a) Взаимодействие скорости вращения и межосевого расстояния установки на PCD; (b) взаимодействие скорости вращения и рабочей скорости на PCD.
Как иллюстрируется на Рисунке 11а, когда межосевое расстояние установки фиксировано, а рабочая скорость находится на начальном этапе, SCR уменьшается с увеличением скорости вращения. Однако по мере роста рабочей скорости SCR сначала уменьшается, а затем увеличивается, в конечном итоге демонстрируя общую восходящую тенденцию и значительно улучшая эффективность очистки от соломы. Когда скорость вращения находится на начальном этапе, SCR уменьшается по мере увеличения рабочей скорости. По мере дальнейшего роста скорости вращения SCR показывает явную тенденцию к увеличению из-за усиленной режущей способности для соломы. Дополнительно, как показано на Рисунке 11b, когда рабочая скорость удерживается постоянной, а межосевое расстояние установки находится в исходном состоянии, SCR значительно увеличивается с ростом скорости вращения. Однако по мере увеличения межосевого расстояния установки SCR сначала увеличивается, а затем уменьшается с дальнейшим увеличением скорости вращения. При низких скоростях вращения SCR сначала уменьшается, а затем увеличивается по мере роста межосевого расстояния установки. По мере дальнейшего роста скорости вращения SCR демонстрирует тенденцию сначала к уменьшению, а затем к увеличению с увеличением межосевого расстояния установки, в конечном итоге показывая общую тенденцию к снижению.
Как показано на Рисунке 12а, когда межосевое расстояние установки фиксировано, а рабочая скорость находится в исходном состоянии, PCD увеличивается со скоростью вращения. Однако по мере роста рабочей скорости PCD продолжает увеличиваться со скоростью вращения, в конечном итоге испытывая значительный скачок. При более низких скоростях вращения, как показано на Рисунке 12b, PCD уменьшается по мере увеличения рабочей скорости. По мере дальнейшего увеличения скорости вращения PCD сначала уменьшается с ростом рабочей скорости, прежде чем впоследствии увеличиться. Когда рабочая скорость удерживается постоянной, а межосевое расстояние установки находится в исходном состоянии, PCD увеличивается со скоростью вращения. По мере увеличения межосевого расстояния установки PCD показывает существенное увеличение с более высокими скоростями вращения. При более низких скоростях вращения PCD уменьшается по мере увеличения межосевого расстояния установки. Однако по мере дальнейшего роста скорости вращения PCD сначала уменьшается, а затем увеличивается с дальнейшим увеличением межосевого расстояния установки, в конечном итоге приводя к общему увеличению.
3.1.3. Оптимизация параметров и проверка моделированием
Чтобы получить оптимальную комбинацию параметров для устройства, параметры для SCR и PCD были оптимизированы с использованием функции оптимизации в программном обеспечении Design-Expert 12. Ограничения изложены в уравнении (21).
Целевая функция была оптимизирована, давая окончательную комбинацию параметров: рабочая скорость 14 км/ч, скорость вращения 339,2 об/мин и межосевое расстояние 100 см. При этих условиях прогнозируемый SCR составлял 87,1%, а PCD — 1,219 кВт. Для проверки этих результатов было проведено моделирование, достигнув SCR 85,71% и PCD 1,337 кВт. Ошибки относительно прогнозируемых значений составили 1,59% для SCR и 9,68% для PCD, что указывает на хорошее соответствие между экспериментальными и прогнозируемыми значениями.
3.2. Анализ процесса моделирования
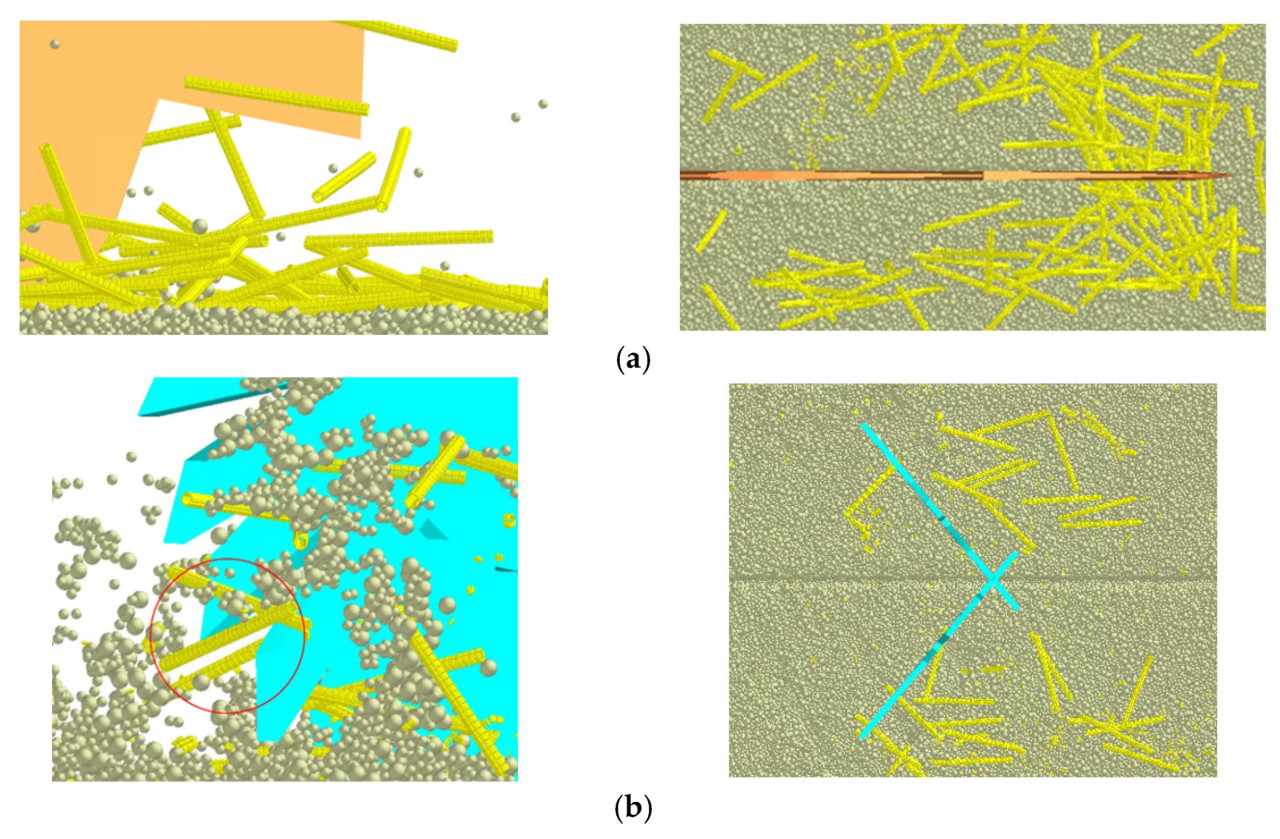
Чтобы дополнительно прояснить взаимодействия между компонентами обработки соломы — соломой и почвой — были проведены моделирования с использованием программного обеспечения EDEM, как иллюстрируется на Рисунке 13. Как показано на Рисунке 13а, соломорезательный диск эффективно режет и рассеивает солому в обе стороны. Во время резки, когда солома контактирует с лезвием, она либо разрезается, либо непосредственно выбрасывается вращением, набирая скорость. После выхода из лезвия солома продолжает свою внешнюю траекторию, образуя узкую очищаемую полосу вдали от положения лезвия, с минимальным количеством соломы, остающейся рядом с лезвием. На Рисунке 13b вращающиеся соломоочистные диски направляют стебли наклонно наружу с обеих сторон, дальнейшим образом расширяя очищенную полосу. Встречное действие соломоочистных дисков создает зону очистки, при этом суженная полоса, создаваемая дисками, повышает эффективность удаления соломы в пределах этой области. Этот результат соответствует анализу в разделе 2.3, иллюстрируя, что метод дискретных элементов эффективно поддерживает оптимизацию устройства.
Рисунок 13. Рабочий процесс. (a) Процесс резки соломы; (b) процесс очистки соломы.
3.3. Полевые испытания
3.3.1. Процесс испытаний
Полевые испытания были проведены для оценки эффективности очистки от соломы и проходимости машины в оптимальных рабочих условиях, как иллюстрируется на Рисунке 14а. Пять тестов были выполнены в пределах рабочей зоны, при этом каждая зона измерения охватывала длину 100 см и ширину одного посевного ряда. Образцы соломы собирались из каждой зоны как до, так и после работы, и их вес записывался, как показано на Рисунке 14b. Проходимость машин орудий оценивалась в соответствии с «Техническими условиями эксплуатации машин для беспахотного посева кукурузы» и «Техническими условиями эксплуатации машин для беспахотного посева», чтобы определить непрерывную и нормальную работу оборудования и оценить уровни забивания во время использования. Испытания состояли из трех операционных проходов по назначенной области измерения 50 м. Проходимость машины считалась удовлетворительной, если не происходило забивания или происходило только незначительное забивание.
Рисунок 14. Полевое испытание. (a) Посевная машина; (b) электронные весы.
3.3.2. Результаты и анализ полевых испытаний
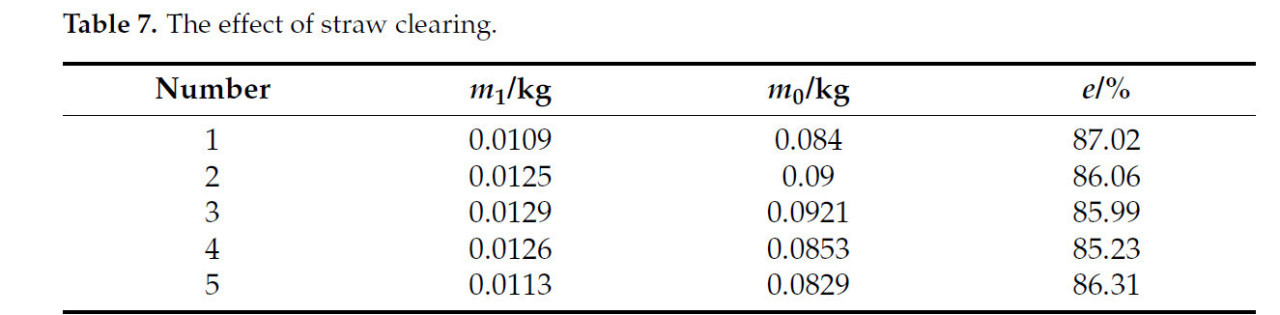
Экспериментальные результаты, полученные после операции, представлены в Таблице 7.
Таблица 7. Эффект очистки соломы.
Анализ указывает на средний коэффициент удаления соломы (SCR) 86,12%. Как иллюстрируется на Рисунке 15, солома между рядами была эффективно очищена, подтверждая прогностическую точность модели взаимодействия солома–почва–орудие. Сеялка продемонстрировала непрерывную и надежную работу во всех трех рабочих процессах. Во время этих процессов солома была эффективно поднята и разбросана за пределы посевных рядов, обеспечивая беспрепятственную работу. Никаких значительных забиваний не наблюдалось по завершении, и машина успешно прошла тест на проходимость.
Рисунок 15. Процесс работы. (a) Процесс резки соломы; (b) рабочие эффекты.
Дополнительно, соломорезательный диск был спроектирован на основе эвольвентной кривой, установка эксцентриситета для простоты изготовления, что может способствовать освобождению соломы после резки. Соломоочистной диск может помочь соломе, обратно засыпаемой после сложного движения, покинуть зону очистки. Они могут быть оптимизированы с использованием методов DEM и планирования эксперимента. Устройство для обработки соломы, интегрированное в сеялку, соответствовало требованиям к семенному ложу для высокоскоростных посевных операций, демонстрируя свою пригодность для эффективной и надежной полевой производительности. Когда количество соломенного покрова неоднородно, более высокий вал орудия может уменьшить запутывание и забивание соломы, а вращение диска помогает разрезать слой соломы и разделить его на две стороны. Поэтому он может адаптироваться к процессам против забивания во многих условиях, но скорость вращения требует дальнейшего изучения.
3.3.3. Обсуждение
Устройство может использоваться в высокоскоростном режиме, функция резки и сгребания ослабляет влияние сложного движения и уменьшает нарушение почвы по сравнению с другими активными устройствами для срезания стерни. Традиционные пассивные диски не обладают достаточной мощностью, чтобы срезать солому в регионе с большим количеством остатков, приводя к слабому рабочему эффекту. Комбинированное устройство для обработки соломы резанием-сгребанием спроектировано путем принятия схемы динамического привода резки соломы, повышая способность обработки соломы в состоянии низкого энергопотребления.
Однако моделирование DEM было реализовано в заданном состоянии почвенных условий и остатков соломы. Дополнительная работа должна учитывать проверку качества посева и эффекта появления всходов после интеграции устройства в посевную систему. Это приблизит устройство к промышленному внедрению и принятию фермерами.
4. Выводы
Чтобы завершить общую структуру комбинированного устройства для обработки соломы резанием-сгребанием, спроектирована режущая кромка соломорезательного диска на основе эвольвентной кривой. Оптимизированы структурные параметры соломоочистного диска. Осуществимость была проверена с помощью теоретических расчетов и анализа процесса резки и очистки соломы. В этом процессе были получены факторы, влияющие на рабочий эффект, что было полезно для дальнейшего улучшения устройства.
Модель уплотненной почвы и модель гибкой соломы были разработаны с использованием модели контакта Edinburgh Elasto-Plastic Adhesion (EEPA) и контактной модели Hertz–Mindlin Bonding V2. Впоследствии была установлена дискретно-элементная модель, интегрирующая взаимодействия между устройством, соломой и почвой. Испытания методом поверхности отклика были проведены на ключевых факторах, влияющих на производительность, включая поступательную скорость, скорость вращения и межосевое расстояние. Дисперсионный анализ (p < 0,05) подтвердил значимость этих факторов. Были разработаны регрессионные модели для SCR и PCD. Анализ поверхности отклика взаимодействий факторов определил оптимальные рабочие параметры машины: поступательная скорость 14 км/ч, скорость вращения 339,2 об/мин и межосевое расстояние установки 100 см.
Моделирование указало на прогнозируемый SCR 87,1% и PCD 1,219 кВт. Проверочное моделирование достигло SCR 85,71% и PCD 1,337 кВт, что привело к ошибкам прогноза 1,59% для SCR и 9,68% для PCD, тем самым демонстрируя точность регрессионной модели. Полевые испытания, проведенные с использованием оптимизированных параметров, достигли SCR 86,12%, указывая на эффективную рабочую производительность. Эти результаты подтверждают эффективность DEM и подхода оптимизации поверхности отклика.
Ссылки
1. Chen, G.L.; Hu, L.; Luo, X.W.; Wang, P.; He, J.; Huang, P.K.; Zhao, R.M.; Feng, D.W.; Tu, T.P. A review of global precision land-leveling technologies and implements: Current status, challenges and future trends. Comput. Electron. Agric. 2024, 220, 108901. [Google Scholar] [CrossRef]
2. Rusu, T. Energy efficiency and soil conservation in conventional, minimum tillage and no-tillage. Int. Soil Water Conserv. Res. 2014, 2, 42–49. [Google Scholar] [CrossRef]
3. Cui, H.X.; Luo, Y.L.; Chen, J.; Jin, M.; Li, Y.; Wang, Z.L. Straw return strategies to improve soil properties and crop productivity in a winter wheat-summer maize cropping system. Eur. J. Agron. 2022, 133, 126436. [Google Scholar] [CrossRef]
4. Wang, Q.J.; Cao, X.P.; Wang, C.; Li, H.W.; He, J.; Lu, C.Y. Research Progress of No/Minimum Tillage Corn Seeding Technology and Machine in Northeast Black Land of China. Trans. Chin. Soc. Agric. Mach. 2021, 52, 1–15. [Google Scholar]
5. He, J.; Li, H.W.; Chen, H.T.; Lu, C.Y.; Wang, Q.J. Research Progress of Conservation Tillage Technology and Machine. Trans. Chin. Soc. Agric. Mach. 2018, 49, 1–19. [Google Scholar]
6. Wang, H.Y.; Chen, H.T.; Ji, W.Y. Design and experiment of cleaning and covering mechanism for no-till seeder in wheat stubble fields. Trans. Chin. Soc. Agric. Eng. 2012, 28, 7–12. [Google Scholar]
7. Wang, Q.J.; Liu, Z.D.; He, J.; Li, H.W.; Li, W.Y.; He, J.H.; Yan, X.L. Design and experiment of chopping-type maize straw returning machine. Trans. Chin. Soc. Agric. Eng. 2018, 34, 10–17. [Google Scholar]
8. Zhao, J.L.; Jia, H.L.; Guo, M.Z.; Jiang, X.M.; Qu, W.J.; Wang, G. Design and experiment of supported roll-cutting anti-blocking mechanism with for no-till planter. Trans. Chin. Soc. Agric. Eng. 2014, 30, 18–28. [Google Scholar]
9. Jiang, J.L.; Gong, L.N.; Wang, D.W.; Wang, G.P. Development and experiment for driving double coulters anti-blockage device of no-till planter. Trans. Chin. Soc. Agric. Eng. 2012, 28, 17–22. [Google Scholar]
10. Zhu, H.B.; Qian, C.; Bai, L.Z.; Zhao, H.R.; Ma, S.A.; Zhan, X.; Li, H. Design and experiments of active anti-blocking device with forward-reverse rotation. Trans. Chin. Soc. Agric. Eng. 2022, 38, 1–11. [Google Scholar]
11. Torotwa, I.; Ding, Q.S.; Makange, N.R.; Liang, L.; He, R.Y. Performance evaluation of a biomimetically designed disc for dense-straw mulched conservation tillage. Soil Tillage Res. 2021, 212, 105068. [Google Scholar] [CrossRef]
12. Guan, C.S.; Fu, J.J.; Xu, L.; Jiang, X.Z.; Wang, S.L.; Cui, Z.C. Study on the reduction of soil adhesion and tillage force of bionic cutter teeth in secondary soil crushing. Biosyst. Eng. 2022, 213, 133–147. [Google Scholar] [CrossRef]
13. Zeng, Z.W.; Chen, Y. Performance evaluation of fluted coulters and rippled discs for vertical tillage. Soil Tillage Res. 2018, 183, 93–99. [Google Scholar] [CrossRef]
14. Godwin, R.J.; ÓDogherty, M.J. Integrated soil tillage force prediction models. J. Terramechanics 2007, 12, 3–14. [Google Scholar] [CrossRef]
15. Matin, M.A.; Fielke, J.M.; Desbiolles, J.M.A. Furrow parameters in rotary strip-tillage: Effect of blade geometry and rotary speed. Biosyst. Eng. 2014, 118, 7–15. [Google Scholar] [CrossRef]
16. Ma, H.Z.; Zhang, P.; Dong, Y.W.; Wang, X.W.; Xia, R.; Li, B. Study on the rigid-discrete coupling effect of scraper conveyor under different chain speed-load conditions. Simul. Model. Pract. Theory 2024, 134, 102943. [Google Scholar] [CrossRef]
17. Horabik, J.; Molenda, M. Parameters and contact models for DEM simulations of agricultural granular materials: A review. Biosyst. Eng. 2016, 147, 206–225. [Google Scholar] [CrossRef]
18. Zeng, Z.W.; Ma, X.; Chen, Y.; Qi, L. Modelling residue incorporation of selected chisel ploughing tools using the discrete element method (DEM). Soil Tillage Res. 2020, 197, 104505. [Google Scholar] [CrossRef]
19. Li, W.X.; Zhang, F.B.; Luo, Z.T.; Zheng, E.L.; Pan, D.C.; Qian, J.; Yao, H.P.; Wang, X.C. Straw movement and flow field in a crushing device based on CFD-DEM coupling with flexible hollow straw model. Biosyst. Eng. 2024, 242, 140–153. [Google Scholar] [CrossRef]
20. Adajar, J.B.; Alfaro, M.; Chen, Y.; Zeng, Z.W. Calibration of discrete element parameters of crop residues and their interfaces with soil. Comput. Electron. Agric. 2021, 188, 106349. [Google Scholar] [CrossRef]
21. Lenaerts, B.; Aertsen, T.; Tijskens, E.; De Ketelaere, B.; Ramon, H.; De Baerdemaeker, J.; Saeys, W. Simulation of grain–straw separation by Discrete Element Modeling with bendable straw particles. Comput. Electron. Agric. 2014, 101, 24–33. [Google Scholar] [CrossRef]
22. Shi, Y.Y.; Jiang, Y.; Wang, X.C.; Thuy, N.T.D.; Yu, H.M. A mechanical model of single wheat straw with failure characteristics based on discrete element method. Biosyst. Eng. 2023, 230, 1–15. [Google Scholar] [CrossRef]
23. Fang, H.M.; Ji, C.Y.; Zhang, Q.Y.; Guo, J. Force analysis of rotary blade based on distinct element method. Trans. Chin. Soc. Agric. Eng. 2016, 32, 54–59. [Google Scholar]
24. Yuan, P.P.; Li, H.W.; Jiang, G.J.; He, J.; Lu, C.Y.; Huang, S.H. Design and Experiment of Straw Cleaning Device for Wide Narrow Maize No-tillage Sowing Strip in Drip Irrigation Area. Trans. Chin. Soc. Agric. Mach. 2021, 52, 43–52. [Google Scholar] [CrossRef]
25. Zhang, S.L.; Jia, X.; Dong, J.X.; Wang, X.Z.; Zhao, H.B.; Chen, X.H.; Zhang, Z.R.; Huang, Y.X.; Shi, J.T. Optimization of operating angles of disc coulters for maize residue management using discrete element method. Comput. Electron. Agric. 2024, 218, 108691. [Google Scholar] [CrossRef]
26. Wu, P.; Chen, Y. Discrete element modelling of the effect of disc angle and tilt angle on residue incorporation resulting from a concave disc. Comput. Electron. Agric. 2024, 224, 109222. [Google Scholar] [CrossRef]
27. Li, X.; Zhang, Y.P.; He, H.J.; Wang, B.; Zhou, H.; Geng, D.Y.; Zhang, Y.Z. Design and Experiment of Row Cleaner with Staggered Disc Teeth for No-Till Planter. Agriculture 2023, 13, 1373. [Google Scholar] [CrossRef]
28. Yao, W.Y.; Zhao, D.B.; Miao, H.Q.; Cui, P.D.; Wei, M.J.; Diao, P.S. Design and Experiment of Oblique Anti-blocking Device for No-tillage Planter with Shallow Plowing Stubble Clearing. Trans. Chin. Soc. Agric. Mach. 2022, 53, 42–52. [Google Scholar] [CrossRef]
29. Huang, Y.X.; Gao, P.Y.; Zhang, Q.K.; Shen, H.; Zhu, R.X.; Shi, J.T. Design and Experiment of Grass-Soil Separation Device with Combination of Stubble Cutting and Grass Guiding Used for No-till Planter. Trans. Chin. Soc. Agric. Mach. 2020, 51, 67–78. [Google Scholar] [CrossRef]
30. Singh, S.; Tripathi, A.; Singh, A.K. Effect of Furrow Opener Design, Furrow Depth, Operating Speed on Soil Characteristics, Draft and Germination of Sugarcane. Sugar Tech. 2017, 19, 476–484. [Google Scholar] [CrossRef]
31. Shi, Y.Y.; Luo, W.W.; Hu, Z.C.; Wu, F.; Gu, F.W.; Chen, Y.Q. Design and Test of Equipment for Straw Crushing with Strip-laying and Seed-belt Classification with Cleaning under Full Straw Mulching. Trans. Chin. Soc. Agric. Mach. 2019, 50, 58–67. [Google Scholar] [CrossRef]
32. Shi, Y.P.; Zhai, C.Y.; Zhu, R.X.; Yan, X.L.; Ge, S.Q.; Li, C.X.; Shi, Y. Design and operating performance of a trapezoidal combination cutterhead. J. Agric. Mech. Res. 2015, 37, 182–187. [Google Scholar] [CrossRef]
33. Quan, L.Z.; Tong, J.; Zeng, B.G.; Chen, D.H. Optimization design of sliding cutting edge curve of corn rootstalk cutting tool. Trans. Chin. Soc. Agric. Eng. 2011, 27, 13–17. [Google Scholar] [CrossRef]
34. Ma, H.L.; Gao, H.W.; Wei, S.Y. Experimental study on the power mathematic model of the oblique driven tooth-disc. Trans. Chin. Soc. Agric. Eng. 2007, 23, 150–153. [Google Scholar]
35. Bai, X.H.; Lin, J.; Lv, C.Y.; Hu, Y.Q. Analysis and experiment on working performance of disc coulter for no-tillage seeder. Trans. Chin. Soc. Agric. Eng. 2014, 30, 1–9. [Google Scholar] [CrossRef]
36. Wang, H.Y.; Chen, H.T.; Ji, W.Y. Anti-blocking Mechanism of Type 2BMFJ-3 No-till Precision Planter for Wheat Stubble Fields. Trans. Chin. Soc. Agric. Mach. 2013, 44, 64–70. [Google Scholar] [CrossRef]
37. Yao, W.Y.; Diao, P.S.; Zhang, Y.P.; Chen, M.Z.; Li, X.R.; Wang, B. Effect of Wheat and Maize Planting Modes on Mechanized Operation in Double Cropping Areas. J. Agric. Mech. Res. 2021, 43, 255–262. [Google Scholar] [CrossRef]
38. Thakur, S.C.; Morrissey, J.P.; Sun, J.; Chen, J.F.; Ooi, J.Y. Micromechanical analysis of cohesive granular materials using the discrete element method with an adhesive elasto-plastic contact model. Granul. Matter 2014, 16, 383–400. [Google Scholar] [CrossRef]
39. Zhao, J.W.; Yu, J.Q.; Sun, K.; Wang, Y.; Liang, L.S.; Sun, Y.C.; Zhou, L.; Yu, Y.J. A discrete element method model and experimental verification for wheat root systems. Biosyst. Eng. 2024, 244, 146–165. [Google Scholar] [CrossRef]
40. Li, S.C.; Diao, P.S.; Zhao, Y.L.; Miao, H.Q.; Li, X.H.; Zhao, H.D. Calibration of discrete element parameter of soil in high-speed tillage. INMATEH Agric. Eng. 2023, 71, 248–258. [Google Scholar] [CrossRef]
41. Wang, X.L.; Zhong, X.K.; Geng, Y.L.; Wei, Z.C.; Hu, H.; Geng, D.Y.; Zhang, X.C. Construction and parameter calibration of the nonlinear elastoplastic discrete element model for no-tillage soil compaction. Trans. Chin. Soc. Agric. Eng. 2021, 37, 100–107. [Google Scholar] [CrossRef]
42. Xie, F.P.; Wu, Z.Y.; Wang, X.S.; Liu, D.W.; Wu, B.; Zhang, Z.Z. Calibration of discrete element parameters of soils based on unconfined compressive strength test. Trans. Chin. Soc. Agric. Eng. 2020, 36, 39–47. [Google Scholar]
43. Li, S.C.; Diao, P.S.; Miao, H.Q.; Zhao, Y.L.; Li, X.H.; Zhao, H.D. Modeling the fracture process of wheat straw using a discrete element approach. Powder Technol. 2024, 439, 119726. [Google Scholar] [CrossRef]
Li S, Diao P, Li X, Zhao Y, Zhao H. Design and Optimization for Straw Treatment Device Using Discrete Element Method (DEM). Agriculture. 2025; 15(2):152. https://doi.org/10.3390/agriculture15020152
Перевод статьи «Design and Optimization for Straw Treatment Device Using Discrete Element Method (DEM)» авторов Li S, Diao P, Li X, Zhao Y, Zhao H., оригинал доступен по ссылке. Лицензия: CC BY. Изменения: переведено на русский язык
Фото: freepik
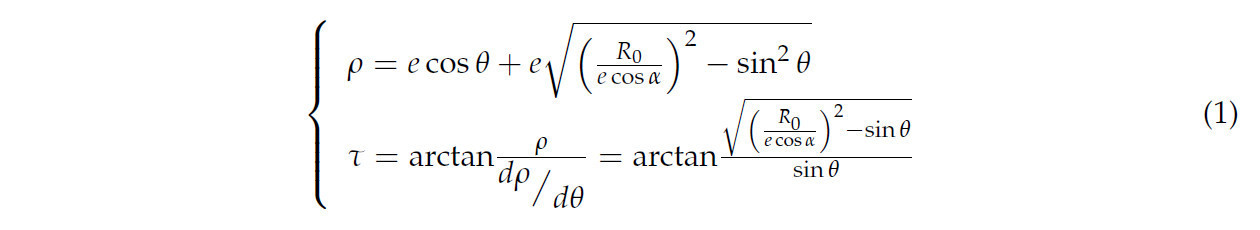
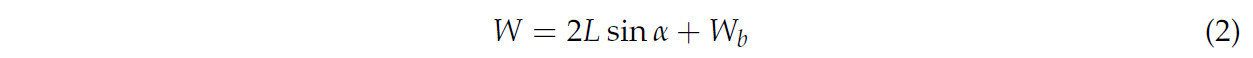
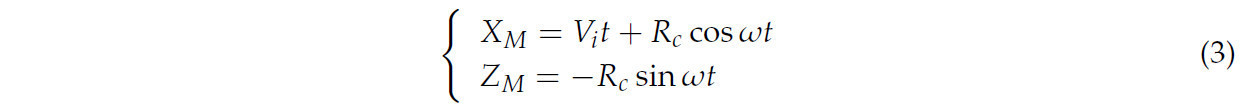
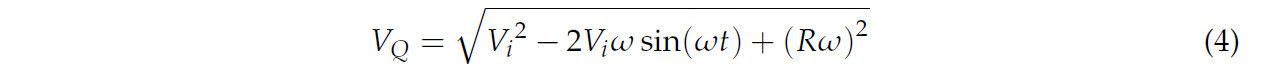
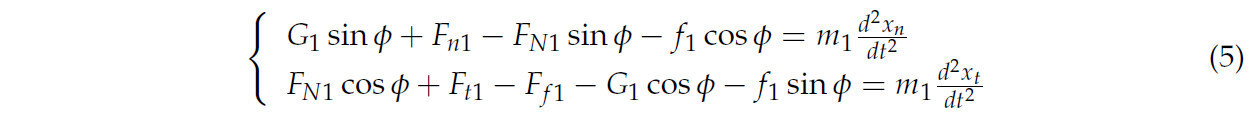
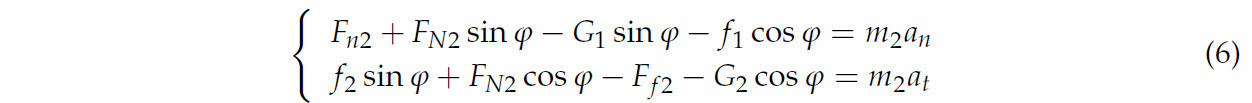
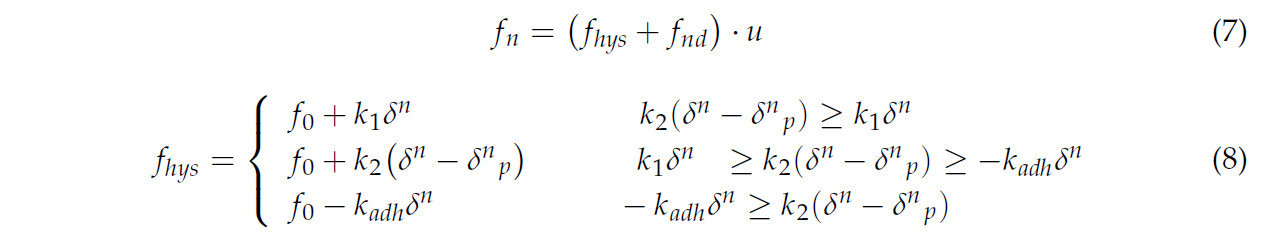
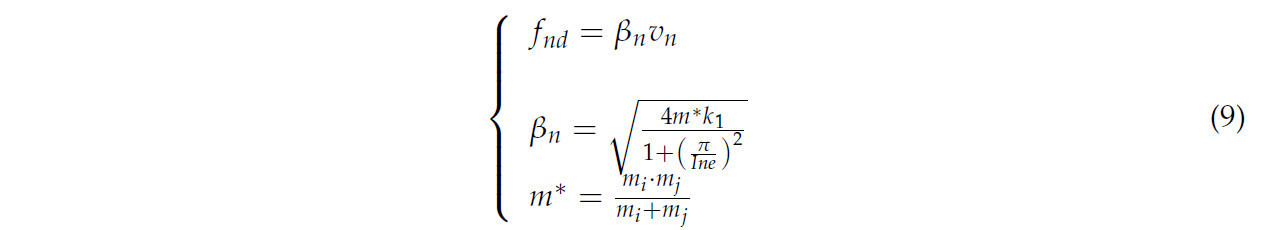
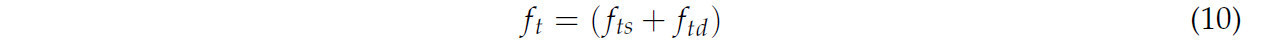
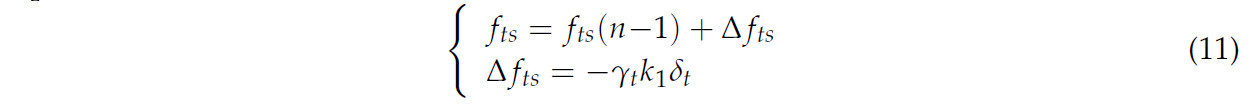
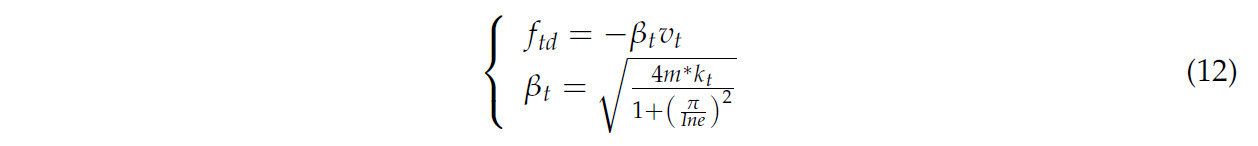
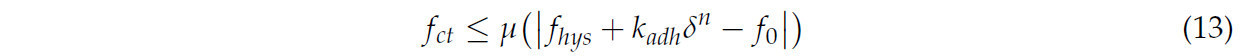

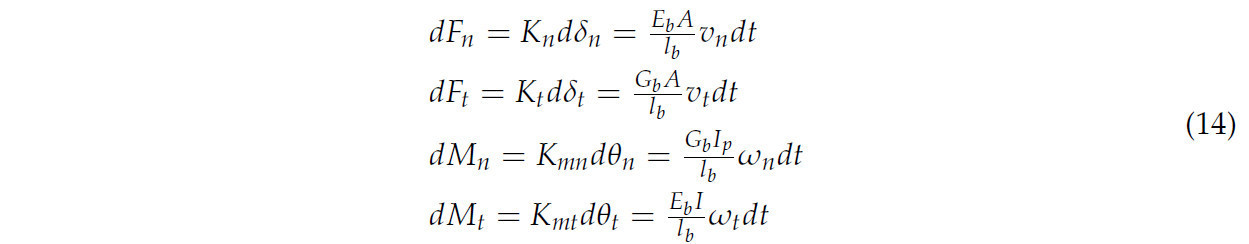
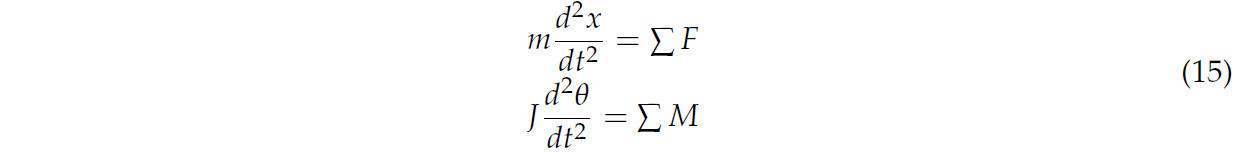
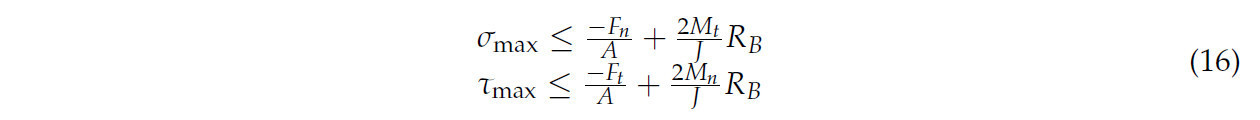


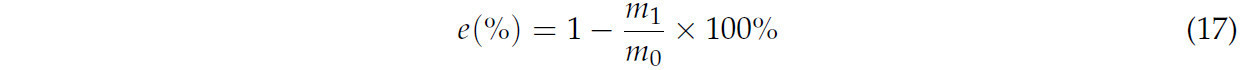
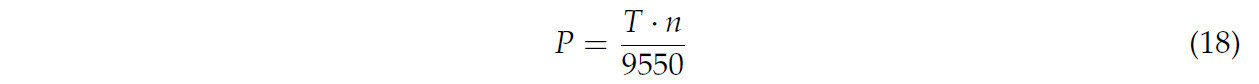
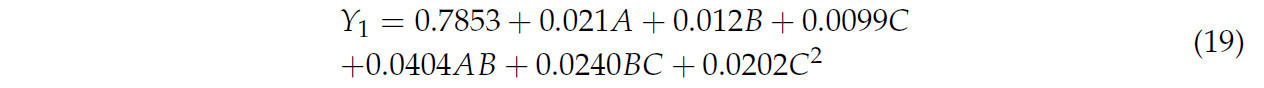
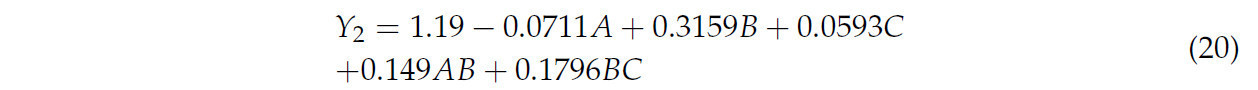
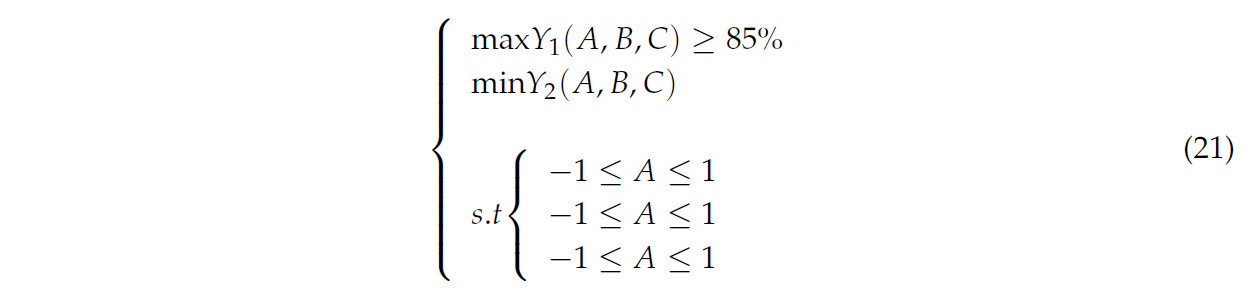
































































































Комментарии (0)