Дефицит воды угрожает урожаю. Как его преодолеть? Модель прогнозирования для сельского хозяйства
Цзянханьская равнина (JHP) является ключевым сельскохозяйственным регионом Китая, где эффективное использование водных ресурсов в сельском хозяйстве (AWUE) имеет жизненно важное значение для устойчивого управления водными ресурсами, продовольственной безопасности, экологической устойчивости и экономического роста. В данном исследовании представлена новая модель прогнозирования AWUE для JHP, сочетающая нейронную сеть BP с алгоритмом поиска воробьев (SSA) и улучшенным алгоритмом смешивания Tent (Tent-SSA-BPNN). Эта гибридная модель преодолевает ограничения традиционных методов, повышая точность и стабильность прогноза AWUE.
Аннотация
Интегрируя исторические данные AWUE и факторы окружающей среды, модель обеспечивает детальное понимание пространственных и временных вариаций AWUE. По сравнению с традиционными нейронными сетями BP и другими методами, модель Tent-SSA-BPNN значительно улучшает точность и стабильность прогнозирования, достигая точности (ACC) 96,218%, среднеквадратичной ошибки (RMSE) 0,952 и коэффициента детерминации (R²) 0,9939, превосходя предыдущие модели. Результаты показывают, что (1) с 2010 по 2022 год средний показатель AWUE на JHP колебался в определенном диапазоне, демонстрируя снижение на 0,69%, с существенными различиями в пространственно-временном распределении по различным городам; (2) точность (ACC) модели прогнозирования Tent-SSA-BPNN составила 96,218%, среднеквадратичная ошибка (RMSE) — 0,952, а значение коэффициента детерминации (R²) — 0,9939. (3) По сравнению с дооптимизационной моделью, значения ACC, RMSE и R² модели Tent-SSA-BPNN значительно улучшились с точки зрения точности и стабильности, что явно указывает на эффективность оптимизации. (4) Результаты прогнозирования показывают, что доля водопотребления в сельском хозяйстве оказывает существенное влияние на AWUE. Эти результаты предоставляют практическую информацию для оптимизации распределения водных ресурсов, особенно в регионах с дефицитом воды, и направляют политиков в улучшении стратегий управления водными ресурсами в сельском хозяйстве, способствуя устойчивому развитию сельского хозяйства.
1. Введение
На Цзянханьской равнине (JHP) ежегодная нехватка водных ресурсов в последние годы привела к снижению урожайности сельскохозяйственных культур до 20%, что наглядно показывает настоятельную необходимость улучшения эффективности использования водных ресурсов в сельском хозяйстве (AWUE). Водные ресурсы, являясь критически важным фактором производства сельскохозяйственных культур, необходимы для устойчивых продовольственных систем. Их эффективное использование не только жизненно важно для повышения производительности сельского хозяйства, но и соответствует глобальным целям устойчивого развития, в частности тем, которые изложены в Целях устойчивого развития (SDG) Организации Объединенных Наций, таких как SDG 2 (Ликвидация голода) и SDG 6 (Чистая вода и санитария) [1]. Эффективное управление водными ресурсами имеет ключевое значение для решения насущных глобальных проблем, таких как продовольственная безопасность, адаптация к изменению климата и устойчивость сельского хозяйства. Однако такие регионы, как JHP, со своими специфическими климатическими и гидрологическими характеристиками, представляют особые проблемы по сравнению с более умеренными или засушливыми зонами. В то время как засушливые регионы сосредоточены на сохранении воды и эффективных методах орошения, а умеренные регионы сталкиваются с умеренной изменчивостью количества осадков, JHP сталкивается с двойной проблемой управления как нехваткой воды в засушливые периоды, так и избытком воды во время сильных дождей, что усложняет разработку устойчивых сельскохозяйственных практик. Эта динамика требует более тонких и адаптируемых стратегий управления водными ресурсами, что делает JHP идеальным объектом для изучения регионов со схожей гидрологической изменчивостью. С учетом прогнозируемого роста мирового населения до более чем 9 миллиардов к 2050 году спрос на водные ресурсы возрастает, в частности в засушливых и полузасушливых регионах, где нехватка воды представляет собой важнейшее ограничение для производительности сельского хозяйства [2]. Эта проблема дальнейшим образом усугубляется изменением климата, которое усиливает частоту и суровость водного стресса, дополнительно подчеркивая необходимость эффективного использования воды в сельском хозяйстве. В частности, Китай, как крупнейшая развивающаяся страна в мире, использует более 60% своих общих водных ресурсов для сельского хозяйства, сталкиваясь с проблемами нехватки воды и неравномерного распределения [3]. JHP, ключевой зернопроизводящий регион в центральном Китае, сталкивается с особыми проблемами управления водными ресурсами в сельском хозяйстве, которые отличают его от других регионов мира. Уязвимость территории к частым стихийным бедствиям, таким как засухи и наводнения, в сочетании со значительными пространственными и временными вариациями в доступности воды усугубляет сложность управления сельскохозяйственными водными ресурсами. В отличие от более умеренных регионов, где доступность воды относительно стабильна, JHP расположена в полувлажной климатической зоне с экстремальными колебаниями водоснабжения, что делает ее более подверженной нехватке воды в засушливые периоды и избытку воды в сезон дождей. Эта уникальная гидрологическая изменчивость в сочетании с быстрой урбанизацией и растущим спросом на воду усиливает необходимость эффективного использования воды и целенаправленных стратегий управления. Следовательно, оптимизация управления водными ресурсами в JHP не только решает локальные сельскохозяйственные и экономические проблемы, но и дает информацию, применимую к другим регионам, сталкивающимся с аналогичными проблемами водного стресса во всем мире. Учитывая критическую важность воды для сельскохозяйственного производства в регионе, уникальные проблемы управления водными ресурсами в JHP — отмеченные колебаниями водоснабжения и растущим спросом — подчеркивают настоятельную необходимость целенаправленных исследований AWUE. Решение этих проблем через эффективное использование воды жизненно важно не только для обеспечения продовольственной безопасности и стабильного производства сельскохозяйственных культур на JHP, но и служит моделью для других полувлажных и вододефицитных регионов мира. Следовательно, оценка и прогнозирование AWUE на JHP имеют как теоретическую, так и практическую ценность для руководства научным управлением и оптимизацией региональных водных ресурсов, а также дают представление об устойчивом использовании водных ресурсов в аналогичных регионах по всему миру.
AWUE — это показатель урожайности сельскохозяйственных культур или экономической ценности, которая может быть произведена на единицу воды в производстве сельскохозяйственных культур [4]. Проведение оценки AWUE способствует разработке и внедрению эффективных стратегий управления водными ресурсами, оптимизируя использование сельскохозяйственных водных ресурсов и повышая производительность сельскохозяйственного производства [5]. Недавние исследования AWUE в основном опирались на показатели общей факторной эффективности, используя модели анализа эффективности, такие как анализ оболочки данных (DEA) [6,7,8], анализ стохастической границы (SFA) [9,10,11] и модели Super-Efficiency SBM (SE-SBM) [12]. Например, Mu и др. использовали модель SE-DEA для измерения уровней AWUE в муниципалитетах Северо-Западного региона [7]; Riera и Bruemmer применили модель SFA для оценки уровней AWUE в бассейне реки Кришна [13]; а Zhi и др. использовали ненаправленную функцию расстояния для оценки уровней AWUE в городской агломерации Бохайского региона [14]. Однако эти модели имеют присущие им ограничения: DEA не учитывает случайные ошибки и чувствительна к выбору входных и выходных данных [15], тогда как SFA требует больших наборов данных и предполагает постоянную техническую эффективность, что может быть неприменимо во всех условиях [16]. Модель SE-SBM, также известная как мера на основе нерационального использования (slacks-based measure) со сверхэффективностью, представляет собой непараметрический метод, используемый для оценки эффективности принимающих решения единиц (DMU), особенно при наличии нежелательных выходных данных. Модель SE-SBM, которая учитывает как желаемые выходные данные (например, урожайность сельскохозяйственных культур), так и нежелательные выходные данные (например, выбросы углерода), предлагает более комплексную основу для оценки AWUE, охватывая как экономические, так и экологические аспекты использования воды в сельском хозяйстве [17]. Более того, она может быть адаптирована к различным структурам и масштабам данных, что делает ее универсальным инструментом для оценки AWUE в различных регионах. Следовательно, в данной статье оценивается AWUE и анализируются ее временные и пространственные характеристики путем построения системы индексов оценки AWUE и выбора модели SE-SBM для научной оценки.
Проведение прогнозов AWUE и создание научной прогнозной модели может предоставить теоретическую поддержку для достижения устойчивого использования водных ресурсов [18]. В настоящее время большинство прогнозов, связанных с эффективностью использования воды (WUE), сосредоточены на эффективности роста растений [19], эффективности использования воды [20] и несущей способности водных ресурсов [21], при этом несколько исследований посвящено AWUE. Учитывая ограничения традиционных методов прогнозирования в водохозяйственных системах, в данной статье разработана новая прогнозная модель для AWUE в JHP, сочетающая сильные стороны модели SE-SBM для оценки AWUE с нейронной сетью BP (BPNN), оптимизированной с помощью алгоритма поиска воробьев (SSA). Модель BPNN, которая обозначает нейронную сеть с обратным распространением ошибки, представляет собой многослойную нейронную сеть прямого распространения, обучаемую с помощью алгоритма обратного распространения ошибки. Также вводится метод хаотического отображения Тента (Tent chaotic mapping). Хаотическое отображение Тента — это тип хаотического отображения, которое проявляет сложное апериодическое поведение через простое уравнение и чрезвычайно чувствительно к начальным условиям, что делает его потенциально полезным в таких областях, как безопасность и эффективная передача большой мощности [22]. SSA — это новый алгоритм оптимизации роевого интеллекта, вдохновленный поведением воробьев при поиске пищи и защите от хищников. Он моделирует биологические групповые характеристики поведения воробьев при поиске пищи и защите от хищников, направлен на решение глобальной проблемы оптимизации с высокой точностью и эффективностью [23]. Этот интегрированный подход устраняет недостатки традиционных моделей, повышая точность и стабильность прогнозирования в сложных нелинейных системах. В настоящее время для прогнозирования водных ресурсов в основном используются традиционные модели [24,25], включая модели серого прогнозирования [26,27] и модели регрессионного анализа. Традиционные прогнозные модели часто не обладают гибкостью при решении сложностей и динамики реального мира. Хотя традиционные прогнозные модели могут давать лучшие результаты в определенных условиях, их точность (ACC) часто не достигает удовлетворительного уровня при столкновении со сложностями реального мира [28,29]. В сложных нелинейных хаотических системах, таких как водохозяйственные системы, традиционные модели с возможностями линейной аппроксимации демонстрируют ограниченную объяснительную способность, что приводит к неоптимальной подгонке модели и снижению достоверности и ACC в прогнозировании выбросов углерода [30]. Чтобы устранить ограничения традиционных методов прогнозирования, исследователи начали применять модели интеллектуальных алгоритмов, в частности модели нейронных сетей (NN), для прогнозирования водохозяйственных систем. Нейронные сети могут автоматически обучаться извлекать признаки из исходных данных, тем самым сводя к минимуму необходимость ручного конструирования признаков. Способность нейронных сетей улавливать и моделировать сложные нелинейные зависимости имеет критическое значение в AWUE, поскольку факторы, влияющие на эффективность, обычно нелинейны и многомерны [31]. В настоящее время многие исследователи проводили исследования прогнозирования с помощью NN в сельском хозяйстве [32], промышленности [33] и энергетике [34], демонстрируя, что прогнозы моделей NN часто превосходят традиционные линейные модели. Однако не было исследований, использующих NN для комплексного прогнозирования AWUE. Возможные причины включают склонность модели NN сходиться к локальным оптимумам, что делает обеспечение точности и стабильности результатов прогнозирования в сложных водохозяйственных системах сложной задачей [35]. Дополнительно, модель NN требует значительного количества образцов для предварительного обучения, тогда как учет водных ресурсов обычно охватывает годы с меньшим количеством образцов данных, что приводит к присущим ограничениям в размере выборки и снижению достоверности результатов прогнозирования [36]. Применяя оптимизированную модель BPNN, данное исследование направлено на значительное улучшение точности и надежности прогнозов AWUE, предлагая ценную информацию для регионального управления водными ресурсами и разработки политики. Сначала SE-SBM измеряет AWUE на Цзянханьской равнине, затем строится модель NN на основе результатов учета и соответствующих переменных прогнозирования AWUE. Затем модель NN оптимизируется с помощью SSA, завершаясь использованием оптимизированной NN для прогнозирования AWUE.
Оставшаяся часть статьи организована следующим образом. Разделы 2.1 и 2.2 описывают объекты исследования и область исследования. Разделы 2.3–2.6 описывают процессы моделирования для метода SE-SBM, хаотического отображения Тента, BPNN, k-кратной перекрестной проверки, SSA и Tent-SSA-BPNN. В разделе 3 подробно измеряется AWUE JHP, и проводится пространственно-временной анализ с помощью метода естественных разрывов (NBM), стандартного эллипса отклонения (SDE), индекса Морана (MI) и модели центра тяжести (CGM). Затем прогнозная модель подвергается анализу корреляции переменных, настройке и обучению параметров NN, сравнению результатов прогнозирования, перекрестной проверке NN и оценке производительности. Наконец, проверенная модель Tent-SSA-BPNN используется для прогнозирования AWUE Цзянханьской равнины. Разделы 4 и 5 предоставляют обсуждение результатов и краткое резюме. Технологическая дорожная карта этого исследования представлена на рисунке 1.
Рисунок 1. Схема исследовательской структуры.
2. Материалы и методы
2.1. Область исследования
JHP — это значительный географический регион в Китае, расположенный в среднем течении реки Янцзы и охватывающий южно-центральную часть провинции Хубэй, которая включает такие районы, как Цзинчжоу, Сяньтао, Цяньцзян и Тяньмэнь. Этот регион известен своей плодородной землей и обильными водными ресурсами и служит одной из ключевых баз производства продовольствия в Китае [37]. Географические особенности JHP включают низкий, плоский рельеф; густую сеть рек; многочисленные озера; и обильные водные системы, что создает благоприятные условия для развития сельского хозяйства [38,39]. Данное исследование сосредоточено на восьми городских административных единицах уровня города, а именно: Ухань, Ичан, Цзинмэнь, Сяогань, Цзинчжоу, Сяньтао, Цяньцзян и Тяньмэнь (Рисунок 2).
Рисунок 2. Область исследования.
2.2. Источники данных
Данные, представленные в этой статье, в основном получены из восьми городов JHP за период 2008–2022 годов, и данные исследования в основном происходят из Китайского статистического ежегодника, Китайского статистического ежегодника водных ресурсов, Китайского сельского статистического ежегодника, Китайского статистического ежегодника по окружающей среде, Китайской базы данных учета углерода, данных Национального статистического бюро, Статистического ежегодника восьми городов JHP и Бюллетеня водных ресурсов за период 2008–2021 годов. Период 2008–2022 годов был выбран из-за наличия последовательных и всеобъемлющих данных в этот период времени, что позволяет анализировать недавние тенденции и изменения в AWUE. Дополнительно, этот период охватывает значительные изменения политики и климатические события, которые могли повлиять на управление водными ресурсами и AWUE на Цзянханьской равнине, тем самым предоставляя релевантный контекст для исследования. Хотя эти источники разнообразны и авторитетны, важно признать потенциальные ограничения. Статистика, публикуемая правительством, может быть подвержена ошибкам отчетности или несогласованностям из-за различных методологий сбора данных в разные годы и районы. Кроме того, использование линейной интерполяции и методов линейного тренда для оценки отсутствующих данных может внести неопределенности, потенциально влияя на надежность результатов. Чтобы смягчить эти проблемы, в исследовании используются методы проверки данных и анализа чувствительности для оценки устойчивости результатов к проблемам качества данных. Данные за некоторые годы остаются неопубликованными из-за правительственных ограничений, а данные по некоторым показателям отсутствуют. Отсутствующие данные были оценены и интерполированы с помощью линейной интерполяции и методов линейного тренда.
2.3. Создание системы показателей для оценки эффективности использования воды в сельском хозяйстве
В данном исследовании создана система оценки AWUE в JHP. Данные, используемые в этом исследовании, были собраны из официальных сельскохозяйственных отчетов и региональной статистики за период 2008–2022 годов. Набор данных охватывает различные регионы JHP, включая как городские, так и сельские районы, и включает данные на уровне провинций. Пространственное разрешение данных основано на административных границах, причем для оценки AWUE используются годовые данные. Данные были предварительно обработаны для удаления выбросов и отсутствующих значений, обеспечивая их надежность для анализа. Шаги очистки данных включали удаление экстремальных выбросов на основе пороговых значений сельскохозяйственного производства и использования воды и импутацию отсутствующих значений с помощью методов интерполяции. В предыдущих исследованиях [40,41,42] была разработана следующая система индексов оценки вход-выход для AWUE, как показано в таблице 1.
Таблица 1. Выбранные показатели для оценки AWUE.
В качестве входных данных были выбраны следующие показатели: площадь основных сельскохозяйственных угодий как показатель земельных затрат, сельскохозяйственное водопотребление и экологическое водопотребление как показатели водных ресурсов, сельскохозяйственная рабочая сила как показатель трудовых затрат, общая мощность сельскохозяйственной техники на конец года как показатель технического прогресса и количество применяемых сельскохозяйственных материалов как показатель капитальных затрат. Ожидаемым выходным показателем является валовая стоимость сельскохозяйственной производства (GVA), которая комплексно отражает использование водных ресурсов в процессе производства сельскохозяйственных культур и тесно связана с экономическими результатами сельского хозяйства. Переменные, выбранные для этого исследования, были основаны на ключевых показателях AWUE, включая площадь сельскохозяйственных угодий, сельскохозяйственное водопотребление и сельскохозяйственную рабочую силу. Набор данных включает годовые данные с 2010 по 2022 год, причем каждая выборка представляет конкретный год для данного региона в пределах JHP. Всего было рассмотрено 13 региональных единиц, причем для каждого региона за годы было собрано несколько выборок, чтобы позволить проводить межгодовые сравнения. Желаемым выходным показателем является общая стоимость сельскохозяйственной производства, которая комплексно отражает использование водных ресурсов в сельскохозяйственном производстве и тесно связана с экономическими результатами сельского хозяйства, тем самым значительно указывая на экономические выгоды от использования сельскохозяйственных водных ресурсов. Нежелательным выходным показателем являются общие выбросы углерода в сельском хозяйстве, определяемые как сумма выбросов углекислого газа, образующихся в процессе сельскохозяйственного производства [43]. Использование общих сельскохозяйственных выбросов углерода в качестве нежелательного выходного показателя улучшает понимание и повышение эффективности сельскохозяйственных водных ресурсов, а также отражает экологические эффекты и воздействие на окружающую среду использования водных ресурсов. Этот подход поддерживает цели устойчивого сельскохозяйственного развития и защиты окружающей среды. В данной статье используется формула выбросов углерода в сельском хозяйстве, применявшаяся в предыдущих исследованиях [44,45]. Формула оценки выбросов углерода следующая:
где представляет общие выбросы углерода от сельского хозяйства, обозначает выбросы углерода из различных источников углерода, указывает количество каждого источника углерода, и относится к коэффициенту выбросов углерода для каждого источника углерода. Выявленные источники углерода включают удобрения, пестициды, сельскохозяйственную пленку, дизельное топливо, орошение и вспашку. Коэффициенты выбросов углерода в сельском хозяйстве были получены путем количественного определения и стандартизации различных источников выбросов углерода в сельскохозяйственной деятельности со значениями 0,8956, 4,9341, 5,18, 0,5927, 20,476 кг/га и 312,6 кг/км² соответственно.
2.4. Модель суперэффективности на основе нерационального использования (SE-SBM)
Модель суперэффективности на основе нерационального использования (SE-SBM) — это непараметрический метод оценки эффективности принимающих решение единиц (DMU), учитывающий нежелательные выходные данные [46]. Модель SE-SBM является надежным инструментом для оценки эффективности; интегрируя концепцию сверхэффективности, она может более точно различать различия в эффективности между DMU, тем самым предоставляя уточненную основу для принятия решений [47]. Модель SE-SBM была реализована с помощью Python 3.7 с библиотекой pyDEA для анализа эффективности. Модель запускалась на компьютере с процессором Intel i7 и 16 ГБ оперативной памяти. Модель SE-SBM выражается следующим образом:
Где 𝜑кт представляет собой показатель AWUE k -го DMU в t -м периоде. Если 𝜑кт<1, то подразделение, принимающее решения, считается неэффективным; если 𝜑кт≥1 означает, что устройство считается эффективным. Большее значение 𝜑кт<1 указывает на более высокую эффективность. Здесь, хik, ydpk, yu𝑞𝑘, и 𝜆j обозначают соответственно i-й входной сигнал, p-й желаемый выходной сигнал, q-й нежелаемый выходной сигнал и j-й коэффициент линейной комбинации k-го объекта принятия решений.
2.5. Модель Tent-SSA-BP
Модель Tent-SSA-BP интегрирует три различных метода: хаотическое отображение Тента, SSA и нейронную сеть с обратным распространением ошибки (BPNN). Модель была разработана в две ключевые фазы. В первой фазе хаотическое отображение Тента использовалось для инициализации популяции для SSA из-за его способности повышать разнообразие поиска и избегать локальных оптимумов. Хаотическое отображение Тента — это форма хаотической системы, которая проявляет чувствительную зависимость от начальных условий, что делает ее высокоэффективной для задач глобальной оптимизации, где критически важно избегать локальных минимумов. Предыдущие исследования показали, что хаотические системы, такие как отображение Тента, способны предоставлять более разнообразные и равномерно распределенные начальные популяции, что может улучшить скорость сходимости и общую производительность алгоритмов оптимизации [48]. Более того, хаотическая природа отображения Тента особенно подходит для сложных нелинейных проблем, таких как прогнозирование AWUE, где традиционные методы инициализации могут не эффективно исследовать пространство решений [49]. Вторая фаза включала оптимизацию BPNN с помощью SSA, где веса и смещения сети корректировались итеративно на основе результатов поиска SSA. Производительность BPNN оценивалась с помощью обучающего набора данных с 2010 по 2020 год, а тестирование модели проводилось с данными за 2021–2022 годы. Эта модель оптимизирует веса и смещения BPNN путем введения хаотического отображения Тента, тогда как динамика популяции SSA дальнейшим образом улучшает оптимизацию параметров сети. Синтезируя сильные стороны этих трех методологий, модель направлена на повышение производительности BPNN в задачах регрессионного прогнозирования. Вычисления для оптимизации и прогнозирования с помощью модели Tent-SSA-BPNN были выполнены в MATLAB R2020a с пользовательскими скриптами, разработанными для обучения и оценки модели. Процесс обучения выполнялся на системе с GPU NVIDIA GTX 1080 для ускорения обучения нейронной сети.
2.5.1. BPNN (Нейронная сеть с обратным распространением ошибки)
BPNN — это модель нейронной сети (NN), которая обучается с помощью алгоритма обратного распространения ошибки [50]. Модель отображает входные данные на выходные данные через связи и вычисления между несколькими слоями нейронов, настраивая веса и смещения во время обучения с помощью алгоритма обратного распространения ошибки, чтобы минимизировать ошибку между прогнозируемыми и фактическими выходными данными [51].
2.5.2. Выбор переменных
Выбор переменных для прогнозирования эффективности AWUE был основан на нескольких критериях. Во-первых, переменные-предикторы должны быть репрезентативными для ключевых факторов, влияющих на эффективность использования воды в сельском хозяйстве в JHP. Выбранные переменные включают водные ресурсы на душу населения (WRPCs), долю поверхностного водоснабжения (SCWS) и долю сельскохозяйственного водопотребления (SAWC). Эти переменные были выбраны потому, что они непосредственно отражают доступность водных ресурсов и распределение воды между сельскохозяйственным и другими видами использования, что является решающим фактором AWUE в регионе. Дополнительно, эти показатели легко доступны из надежных государственных источников данных, что повышает достоверность и точность модели. Корреляция между этими переменными и AWUE была подтверждена в предыдущих исследованиях, которые продемонстрировали их важность в объяснении вариаций эффективности использования воды в сельском хозяйстве [52]. Более того, количество переменных-предикторов должно быть ограничено, поскольку размер выборки для эффективности AWUE относительно мал, и чрезмерное количество переменных может привести к недообучению или переобучению модели. Следовательно, в данной статье предлагается использование трех показателей: водных ресурсов на душу населения (WRPCs), доли поверхностного водоснабжения (SCWS) и доли сельскохозяйственного водопотребления (SAWC) в качестве переменных-предикторов для построения BPNN. Чтобы проверить обоснованность выбора водных ресурсов на душу населения JHP, SCWS относительно общего водоснабжения и SAWC относительно общего водопотребления в качестве входных переменных, необходимо проанализировать корреляцию между этими входными переменными и выходными переменными. Метод коэффициента корреляции Спирмена служит непараметрической мерой корреляции, оценивая связь между рангами двух переменных, а не фактическими значениями переменных [53,54]. Этот метод особенно применим, когда данные не соответствуют нормальному распределению или когда данные иерархичны. Коэффициент корреляции Спирмена рассчитывается следующим образом:
где R представляет коэффициент корреляции Спирмена, D обозначает разницу в ранге между каждой парой данных, и n указывает общее количество образцов. Значения R варьируются от −1 до 1, где R = 1 указывает на идеальную положительную корреляцию, R = −1 означает идеальную отрицательную корреляцию, и R = 0 означает отсутствие корреляции.
Чтобы смягчить эффекты мультиколлинеарности между переменными, необходимо проанализировать корреляцию между входными переменными [55]. Метод фактора инфляции дисперсии (VIF) используется для измерения степени ковариации между переменными и рассчитывается следующим образом [56,57]:
где VIF представляет фактор инфляции дисперсии, x1 обозначает переменную 1, x2 обозначает переменную 2, x3 обозначает переменную 3, и R2 указывает коэффициент детерминации.
2.5.3. Выбор оценочных показателей
Оценка прогностической эффективности нейронных сетей (NN) обычно включает несколько метрик, которые предоставляют комплексный обзор производительности модели [58]. Оценочные метрики, выбранные в данной статье, включают точность (ACC), среднеквадратичную ошибку (RMSE) и коэффициент детерминации (R2). ACC измеряет точность прогнозов модели классификации, указывая долю образцов, правильно классифицированных моделью [59]. RMSE количественно определяет прогностическую точность модели регрессии, вычисляя квадратный корень из среднего значения квадратов разностей между прогнозируемыми и фактическими значениями модели [60]. Коэффициент детерминации (R2) оценивает качество подгонки модели регрессии, указывая, насколько хорошо модель объясняет изменчивость данных [61]. Формулы для трех показателей представлены ниже:
где n представляет размер выборки набора данных, y_i обозначает истинное значение i-го образца, и (y_i ) ̂ указывает прогнозируемое значение i-го образца.
2.6. Методы оптимизации нейронной сети BP
2.6.1. K-Кратная перекрестная проверка (KFCV)
Учитывая ограниченный размер выборки для прогнозирования AWUE, необходимо увеличить выборки обучающего и тестового наборов, разделяя набор данных с помощью k-кратной перекрестной проверки (KFCV) [62]. KFCV — это статистическая методика, используемая для оценки и сравнения производительности моделей машинного обучения. Эта методика делит набор данных на K равных по размеру подмножеств, каждое из которых по очереди служит тестовым набором, а остальные K − 1 подмножеств составляют обучающий набор. Этот процесс повторяется K раз, причем на каждой итерации выбирается различное подмножество в качестве тестового набора [63]. В конечном счете, результаты K оценок усредняются для получения оценки производительности модели. KFCV является надежной методикой оценки модели, которая дает более точные и надежные прогнозные модели для AWUE за счет обширного обучения и проверки.
2.6.2. Традиционный SSA
Традиционные нейронные сети с обратным распространением ошибки (BPNN) сталкиваются с такими проблемами, как локальная оптимизация, исчезающие или взрывающиеся градиенты, длительное время обучения и проблемы в выборе структуры [64]. SSA — это техника оптимизации группового интеллекта, которая имитирует поведение воробьев при поиске пищи и защите от хищников. Основной принцип SSA заключается в использовании взаимодействий и обмена информацией между индивидами в группе для повышения эффективности поиска и идентификации глобального оптимального решения. Традиционный SSA определяется следующим образом:
Шаг 1: Инициализация. Случайным образом генерируются позиции стаи воробьев, каждая из которых представляет потенциальное решение.
Шаг 2: Оценка приспособленности. Значение приспособленности для каждого воробья рассчитывается, обычно на основе целевой функции.
Шаг 3: Обновление лидера (производителя). Лидер обновляет свою позицию согласно следующей формуле:
где X_worst представляет текущую наихудшую позицию, X_P обозначает позицию лидера, A — случайная матрица, A^+ — псевдообратная матрица для A, и L указывает фактор обучения.
Шаг 4: Обновление последователей (присоединяющихся). Последователи корректируют свои позиции на основе местоположения лидера.
где X_best представляет текущую глобальную оптимальную позицию и где β обозначает параметр управления шагом.
Шаг 5: Обновление (Воробей, который воспринимает опасность). Когда воробьи обнаруживают потенциальную угрозу, они принимают стратегию избегания, и формула для обновления их позиции следующая:
где k представляет случайное число, f_i обозначает текущее значение приспособленности воробья, f_w указывает наихудшее значение приспособленности, и ε — малая константа, введенная, чтобы избежать деления на ноль.
Шаг 6: Итерация. Повторяйте шаги 2–5 до тех пор, пока не будут выполнены условия остановки, такие как достижение максимального количества итераций или достижение удовлетворительного качества решения.
Шаг 7: Вывод оптимального решения. После работы алгоритма идентифицируется оптимальное решение.
2.6.3. Оптимизация SSA
Для повышения разнообразия и однородности инициализированной популяции для инициализации популяции используется хаотическое отображение Тента [65]. Интеграция хаотического отображения Тента в алгоритм разреженного поиска (SSA) может значительно улучшить разнообразие и поисковую способность алгоритма, в частности в избегании локальных оптимумов и повышении эффективности глобального поиска [66]. Чтобы дальнейшим образом повысить глобальную точность оптимизации (ACC) алгоритма, в позиции индивидов с различными уровнями приспособленности вводятся возмущения: для индивидов с более высокой приспособленностью применяется гауссовская вариация [67] для корректировки позиции; для индивидов с более низкой приспособленностью используется возмущение Тента [66] для корректировки позиции.
Хаотическое отображение Тента, которое было успешно применено в задачах оптимизации [68], формулируется следующим образом:
где r — параметр хаоса, который обычно принимает значения от 2 до 4, x_n представляет текущее значение итерации, и x_n принимает значения от 0 до 1.
Гауссовская вариация рассчитывается как:
X_new — это новый индивид после мутации. X_old — исходный индивид, и N(μ,σ^2) — нормально распределенное случайное значение со средним μ и дисперсией σ^2. Среднее и дисперсия эквивалентны таковым у исходного индивида.
Для решения проблем SSA, хаотическое отображение Тента, гауссовская вариация и возмущение Тента последовательно вводятся для улучшения, что приводит к конкретным шагам реализации улучшенного Tent-SSA. Конкретные шаги включают настройку параметров, инициализацию, разделение популяции, обновление позиций, перерасчет, возмущение позиций и вывод информации. На основе вышеупомянутой стратегии улучшенного SSA традиционная BPNN оптимизируется для повышения ее сходимости и глобальной поисковой способности, тем самым улучшая ACC и стабильность прогнозирования AWUE. Общий поток оптимизированной модели BPNN (Tent-SSA-BPNN), интегрирующей улучшенный SSA, иллюстрируется на рисунке 3.
Рисунок 3. Блок-схема Tent-SSA-BPNN.
3. Результаты
3.1. Пространственно-временной анализ AWUE в JHP
3.1.1. Изменения во временном измерении AWUE в JHP
В этом исследовании модель SE-SBM использовалась для построения глобальной границы эффективности, и значения AWUE JHP с 2010 по 2021 год были рассчитаны с помощью программного обеспечения MATLAB 2022. Для анализа были выбраны семь репрезентативных лет: значения эффективности и их средние значения по JHP за 2010, 2012, 2014, 2016, 2018, 2020 и 2022 годы (Рисунок 4).
Рисунок 4. Временные тенденции изменения AWUE в JHP, 2010–2022 гг.
Рисунок 4 показывает временные тенденции изменения AWUE в JHP с 2010 по 2022 год. Среднее значение AWUE колебалось в определенном диапазоне, с уменьшением на 0,69% за период исследования. Город Ичан показал самое высокое среднее значение AWUE, равное 1,394, что указывает на более эффективное использование сельскохозяйственной воды, тогда как город Тяньмэнь показал самое низкое среднее значение AWUE, равное 0,464, что предполагает возможности для улучшения использования водных ресурсов. Как важнейший рисоводческий регион Китая, AWUE в JHP имеет значительные последствия для демонстрации и руководства. Результаты, полученные с помощью модели SE-SBM, указывают на то, что AWUE в JHP демонстрировала общую колеблющуюся тенденцию в течение периода исследования, без четкого монотонного увеличения или уменьшения. Увеличение AWUE требует баланса между различными факторами. Например, технологические достижения могут повысить эффективность использования воды; однако они часто требуют увеличения инвестиций в ресурсы и капитал. Следовательно, AWUE может демонстрировать колеблющиеся тенденции из-за компромиссов между различными факторами.
3.1.2. Пространственные измерения AWUE в JHP
Пространственное распределение AWUE в JHP по методу NBM
Чтобы интуитивно проанализировать изменения в пространственном распределении AWUE в городах, результаты были визуализированы с помощью метода естественных разрывов [69] в ArcGIS 10.4, как показано на рисунке 5. Используя NBM вместе с предыдущими исследованиями [70,71], AWUE классифицируется на пять категорий: I (Класс оптимальной эффективности), II (Класс высокой эффективности), III (Класс средней эффективности), IV (Класс низкой эффективности) и V (Класс крайне низкой эффективности).
Рисунок 5. Пространственная дифференциация AWUE в JHP.
Среди городов город Ичан демонстрировал относительно высокую эффективность использования водных ресурсов в течение периода исследования, тогда как город Тяньмэнь и среднее значение были ниже. Пространственные закономерности AWUE в таких городах, как Ухань, Ичан и Сяогань, стабильно улучшались из года в год, отражая эффективные методы управления водными ресурсами. Напротив, города Цзинмэнь и Цзинчжоу показали более колеблющиеся тенденции, на которые могут влиять региональные факторы, такие как изменения в сельскохозяйственных практиках или климатических условиях. Город Ичан стабильно поддерживал относительно высокую эффективность использования водных ресурсов в течение всего периода исследования и занимал первое место в большинстве лет. В период с 2018 по 2021 год Ухань продемонстрировал более высокую AWUE и внедрил более эффективные меры управления водными ресурсами, включая распределение воды, квоты использования, мониторинг и стратегии управления, чтобы обеспечить эффективное использование сельскохозяйственной воды [72]. В городе Ичан AWUE постепенно увеличивалась в последние годы, что отражает улучшения в практике управления водными ресурсами. Однако снижение, наблюдавшееся в 2021 году, подчеркивает важность последовательных методов управления сельским хозяйством, поскольку изменения в методах орошения или земледелия могут влиять на эффективность использования воды [73]. Средние значения для Цзинмэня и Сяогана остаются относительно стабильными, но снизились в 2021 году, возможно, из-за необычных климатических событий, таких как уменьшение количества осадков, приводящее к засухе в некоторых районах, или повышенные температуры наводнения [74]. AWUE в Цзинчжоу и Сяньтао показала значительные колебания, которые могут быть связаны с изменениями в структуре сельского хозяйства и моделях возделывания. Эти корректировки, такие как сдвиги в типах культур и методах земледелия, оказывают прямое влияние на эффективность использования сельскохозяйственной воды в этих регионах. В 2018 году город Цзинчжоу реализовал план «Возрождение сельских районов», что привело к изменениям в структуре посевов, включая сокращение площадей, отведенных под зерновые, масличные культуры и хлопок, наряду с увеличением площадей, предназначенных для бахчевых культур, фруктов и овощей. Одновременно город Цзинчжоу продвигал возделывание регенеративного риса и интегрированную модель рисоводства, и к 2020 году ожидается дальнейшее расширение площади, предназначенной для модели земледелия «совместное выращивание креветок и риса». Аналогично, город Сяньтао корректирует свою сельскохозяйственную структуру и модели посадки, продвигая сельскохозяйственную индустриализацию и увеличивая площади, отведенные под овощные сооружения, интегрированное земледелие и аквакультуру [75,76]. Средние значения для города Цяньцзян и города Тяньмэнь также колебались в течение лет, но общая тенденция оставалась относительно стабильной. Однако город Цяньцзян значительно увеличился в 2021 году, при этом технологические достижения и улучшенное управление, вероятно, сыграли ключевую роль [77].
Анализ пространственной дифференциации AWUE в JHP с помощью метода SDE
Используя результаты измерения AWUE в JHP с 2010 по 2022 год, это исследование исследует пространственное распределение AWUE путем применения метода SDE [78]. SDE визуализируют характеристики пространственного распределения данных путем расчета среднего центра, стандартного отклонения и угла поворота набора данных для генерации эллипса [79]. В этом исследовании используются координаты широты и долготы восьми городов на уровне префектуры в JHP, используя AWUE каждого города в качестве весов. Модель SDE вычисляет координаты центра тяжести, стандартные отклонения длинной и короткой полуосей и угол поворота, чтобы тщательно проанализировать направление пространственного распределения AWUE, его динамические характеристики и степень дисперсии в JHP. Координаты центра SDE для каждого года в JHP были рассчитаны с помощью программного обеспечения ArcGIS 10.4, и параметры были сведены в сводную таблицу (Рисунок 6).
Рисунок 6. Анализ данных SDE AWUE в JHP.
Используя шесть точек данных, представленных на рисунке 6, этот анализ исследует характеристики распространения, ориентации и формы эллиптической разности. Анализируя характеристики распространения, площадь эллипса с 2010 по 2022 год сначала увеличивалась, а затем уменьшалась, увеличившись с 238,85 млн квадратных километров в 2010 году до пика в 264,33 млн квадратных километров в 2012 году, прежде чем постепенно снизиться до 261,15 млн квадратных километров в 2022 году. Это изменение предполагает, что AWUE в JHP демонстрировала тенденцию к агломерации и росту в первые годы, но начала оптимизироваться с 2012 года, что отражает снижение степени агломерации. С точки зрения направленных характеристик, угол поворота центральной точки уменьшился с 81,51° в 2010 году до 80,66° в 2022 году, указывая на слабую тенденцию вращения против часовой стрелки; таким образом, направление AWUE в JHP остается относительно стабильным, в основном ориентированным вдоль оси «северо-восток–юго-запад». Что касается характеристик формы, как иллюстрируется на рисунке 7, эллипс демонстрирует более выраженное расширение в направлении X, тогда как изменение в направлении Y относительно минимально. Небольшое изменение угла поворота предполагает небольшое изменение направленной тенденции, указывая на то, что форма эллипсоида становится более сбалансированной и «округлой», отражая ослабление направленной тенденции.
Рисунок 7. Тенденции SDE и CGM для AWUE в JHP.
Метод центроидной геометрии (CGM) используется для анализа характеристик пространственного распределения в региональной экономике путем вычисления средневзвешенного положения экономической деятельности по субрегионам, тем самым определяя центроид этой деятельности [80,81]. Эта модель эффективно отражает тенденции пространственной концентрации и изменения в распределении экономической деятельности, служа надежным инструментом для исследований регионального экономического развития, планирования и разработки политики. Это исследование направлено на изучение характеристик пространственного центра AWUE в JHP с 2010–2021 гг. с помощью экономического CGM и анализ траектории центра тяжести, чтобы понять эволюционные тенденции и разрывы в развитии в пространственном расположении AWUE.
Используя ArcGIS 10.4, был построен центр тяжести AWUE в JHP с 2010 по 2022 год, что показало, что центр тяжести постоянно оставался в городе Тяньмэнь. Траектория миграции указывает на то, что AWUE демонстрировала циклические и нестабильные изменения в течение последних нескольких лет, наряду с заметными разрывами в развитии, с общей тенденцией движения на юго-восток. Конкретная траектория миграции следующая: Северо-Западный Китай (2010–2012) → Восточный Китай (2012–2014) → Северо-Западный Китай (2014–2016) → Юго-Западный Китай (2016–2020) → Юго-Восточный Китай (2020–2022).
Анализ пространственной корреляции на основе подхода индекса Морана (MI)
В этом исследовании использовался MI [82] для оценки как глобальной, так и локальной пространственной корреляции AWUE в JHP. Был рассчитан глобальный MI AWUE в JHP, и результаты представлены в таблице 2. Что касается изменений в значениях глобального MI, значения для JHP демонстрировали волатильность с 2010 по 2021 год. Значение MI −0,091 в 2010 году указывает на небольшую отрицательную пространственную корреляцию, тогда как значения за 2012, 2016 и 2021 годы составляют 0,439, 0,601 и 0,117 соответственно, отражая положительные пространственные корреляции в эти годы и обозначая районы с высокой AWUE. С точки зрения тенденций временных рядов, значения MI для JHP демонстрируют значительную волатильность. Например, более высокие положительные значения в 2012 и 2016 годах означают сильную пространственную агрегацию, тогда как отрицательное значение в 2020 году означает пространственную дисперсию. Z-значения 2,011 и 2,123 для 2012 и 2016 годов соответственно достигли значимости, указывая, что пространственная агрегация была статистически значимой в эти годы. Напротив, Z-значения для других лет были ниже, что предполагает, что пространственная агрегация не была значительной. p-значения 0,050 для 2012 года и 0,029 для 2016 года были ниже или близки к традиционному уровню значимости 0,05, что дальнейшим образом подтверждает вывод о том, что пространственная агрегация была значительной. Более высокие p-значения в другие годы отражали более слабую статистическую значимость. Пространственная корреляция в JHP демонстрировала динамическую тенденцию, что позволяет предположить, что пространственное распределение и взаимодействие AWUE могли находиться под влиянием различных факторов в разные годы.
Таблица 2. Анализ глобального MI AWUE в JHP.
Локальный MI дает представление о локальных характеристиках пространственных данных, связанных с AWUE в JHP, предоставляя основу для дальнейшего пространственного анализа и принятия решений. Используя платформу Geoda, были созданы диаграммы рассеяния индекса Морана для AWUE в JHP за 2012 и 2016 годы (Рисунок 8). Анализ рисунка 8 показывает, что диаграмма рассеяния Морана для AWUE в JHP в основном распределена в первом и третьем квадрантах, демонстрируя характеристики кластеризации среди регионов с аналогичными уровнями AWUE. Это предполагает, что определенные районы JHP эффективно управляют и используют сельскохозяйственные водные ресурсы, что приводит к регионам с эффективным использованием воды. Точки рассеяния в третьем квадранте в основном сгруппированы вокруг регионов, которые эффективно используют сельскохозяйственные водные ресурсы, указывая на пространственную корреляцию между этими районами, что, вероятно, связано с аналогичным распределением ресурсов, мерами политики или структурами сельскохозяйственного производства. Хотя ограниченное количество точек рассеяния находится во втором квадранте, это может указывать на районы с неэффективной AWUE, которые требуют дальнейшего управления и улучшения.
Рисунок 8. Диаграмма рассеяния Морана AWUE в JHP.
Квадранты, соответствующие каждой провинции, нанесены на диаграмму рассеяния MI за 2012 и 2022 годы, представленную в таблице 3. Города классифицируются в различные квадранты на основе их пространственной релевантности. В 2012 году Ухань находился в первом квадранте (высокий-высокий), в то время как Цзинчжоу, Цзинмэнь и Ичан занимали второй квадрант (низкий-высокий); Сяньтао, Цяньцзян и Тяньмэнь были помещены в третий квадрант (низкий-низкий), а Сяогань был найден в четвертом квадранте (высокий-низкий). К 2016 году Ухань и Цзинчжоу продолжали занимать первый квадрант; однако Цзинмэнь, Сяогань, Ичан и Ухань перешли во второй квадрант, тогда как Тяньмэнь, Цяньцзян и Сяньтао остались в третьем квадранте. Это распределение указывает на то, что обратная агломерация стала преобладающим фактором, наряду со значительными пространственными различиями.
Таблица 3. Квадрантная таблица городов на уровне префектуры в JHP.
3.2. Прогнозный анализ AWUE в JHP с помощью Tent-SSA-BPNN
3.2.1. Корреляционный анализ
В этом исследовании были выбраны три показателя в качестве переменных-предикторов: водные ресурсы на душу населения (WRPC), доля поверхностного водоснабжения (SCWS) и доля сельскохозяйственного водопользования (SAWC). Чтобы проверить рациональность выбора водных ресурсов на душу населения, SCWS в общем водоснабжении и SCWS в общем водопользовании в качестве входных переменных, необходимо проанализировать корреляцию между этими входными переменными и выходными переменными. Метод коэффициента корреляции Спирмена использовался для расчета корреляции между тремя показателями и AWUE; результаты представлены в таблице 4. Таблица 4 указывает на то, что AWUE в JHP коррелирует с SCWS. Коэффициенты корреляции 0,822 и 0,903 для SCWS и SAWC соответственно значительны на уровне 1%, указывая на сильную корреляцию между AWUE в JHP и как SCWS, так и SAWC. Таким образом, SCWS и SAWC в качестве входных переменных эффективно отражают изменения эффективности AWUE в JHP. Коэффициент корреляции между AWUE и WRPC в JHP составляет 0,473, тогда как коэффициент корреляции между AWUE и WRPC составляет 0,402, указывая на умеренную корреляцию [83]. Хотя WRPC демонстрирует значительную корреляцию, учитывая ограниченное количество выбранных переменных и его потенциальное влияние на состояние водных ресурсов в реальной производственной деятельности, эта переменная сохраняется в качестве входной переменной.
Таблица 4. Таблица корреляционного анализа.
Метод фактора инфляции дисперсии (VIF) использовался для расчета факторов инфляции дисперсии (VIF) для WRPC, SCWS и SAWC в JHP; результаты представлены в таблице 5. Факторы инфляции дисперсии для трех показателей меньше 10, что указывает на слабую корреляцию между входными переменными и предполагает, что эффект мультиколлинеарности можно не учитывать [84]. Следовательно, эти три показателя могут служить независимыми переменными для прогнозирования AWUE в JHP, что делает модель прогнозирования NN, построенную с WRPC, SCWS и SAWC, перспективным подходом.
Таблица 5. Анализ фактора инфляции дисперсии переменных.
3.2.2. Настройка параметров модели и обучение
Набор данных был случайным образом разделен на пять взаимоисключающих подмножеств, каждое из которых содержало размеры выборки 2, 2, 3, 3 и 3, всего 13 образцов. На каждой итерации различное подмножество назначается в качестве тестового набора, а остальные четыре подмножества служат обучающим набором; этот процесс повторяется пять раз. Входные переменные включают WRPC, SCWS и SAWC, тогда как выходная переменная — AWUE в JHP; все данные нормализуются перед анализом. Функция new используется для установки BPNN; функции активации для скрытого слоя и выходного слоя — это функции Tansig и Purelin соответственно, и алгоритм обучения использует функцию trail, которая интегрирует метод градиентного спуска с методом Гаусса-Ньютона. Учитывая небольшой размер выборки, NN настроена с одним скрытым слоем, и количество нейронов в этом слое определяется путем перебора эмпирического интервала [85,86], где n1 представляет количество входных переменных, и n2 обозначает количество выходных переменных. В сочетании с предыдущими исследованиями максимальное количество эпох обучения для NN установлено на 100, со скоростью обучения 0,01. Дополнительно, размер особи популяции воробьев в SSA установлен на 100, количество итераций установлено на 20, доля открывателей составляет 60%, доля бдительных составляет 20%, а порог предупреждения равен 0,6. Обучение и прогнозирование проводятся после завершения настройки модели в соответствии с вышеупомянутыми параметрами.
3.2.3. Результаты прогнозирования обучения модели
Процесс итерационной сходимости ошибки модели Tent-SSA-BPNN иллюстрируется на рисунке 9. Анализ показывает, что в течение 1-й по 6-ю итерации скорость сходимости ошибки быстрая; с 6-й по 14-ю итерации эта скорость замедляется и приближается к стабильности, потому что модель попадает в локальное оптимальное решение, что приводит к снижению производительности сходимости. С 14-й по 19-ю итерации ошибка уменьшается быстро, и после 20 итераций она стабилизируется и больше не изменяется, что указывает на то, что модель достигла глобального оптимального решения. В целом, модель Tent-SSA-BPNN быстро завершает процесс итерационной сходимости ошибки, указывая на ее сильную производительность сходимости. Более того, модель Tent-SSA-BPNN эффективно выходит из локальных оптимальных решений, подчеркивая ее надежную способность глобальной поисковой оптимизации.
Рисунок 9. График сходимости итераций RSME.
Результаты прогнозирования и относительные ошибки модели Tent-SSA-BPNN для AWUE в JHP представлены в таблице 6, которая указывает, что максимальная относительная ошибка между прогнозируемыми и фактическими значениями составляет 1,808%, тогда как минимальная относительная ошибка составляет 0,362%, и средняя относительная ошибка составляет 0,996%. Ошибка прогнозирования модели Tent-SSA-BPNN для AWUE в JHP значительно меньше 5%, что указывает на то, что модель имеет высокую точность прогнозирования. Рисунок 10 показывает график подгонки прогноза модели. Точечные диаграммы прогнозируемых и фактических значений тесно сгруппированы вокруг линии тренда, с коэффициентом корреляции 0,98851, указывая на сильную корреляцию между прогнозируемыми и фактическими значениями и высокую степень подгонки модели.
Рисунок 10. Степень подгонки прогноза.
Таблица 6. Факторы инфляции дисперсии.
3.2.4. Перекрестная проверка NN
Из-за присущих ограничений прогнозирования AWUE, вытекающих из небольшого размера выборки, результаты индивидуальных прогнозов могут быть случайными и неубедительными. Чтобы повысить достоверность результатов прогнозирования AWUE, используется 5-кратная перекрестная проверка (FFCV) для оценки показателей модели Tent-SSA-BPNN. Каждая точка данных в наборе данных используется как в качестве обучающих, так и в качестве тестовых данных для нескольких проверок, компенсируя ограничения, вызванные небольшим размером выборки при прогнозировании сельскохозяйственных выбросов углерода. Результаты FFCV представлены в таблице 7. Оценка FFCV модели tent-SSA-BPNN для AWUE в JHP дала точность (ACC) 96,218% и среднеквадратичную ошибку (RMSE) 0,952, что указывает на то, что расхождения между прогнозируемыми значениями и фактическими значениями, полученными моделью в различных обучающих и тестовых наборах, минимальны, подтверждая прогностическую способность модели для AWUE. Значение R², полученное из FFCV модели, составляет 0,9939, указывая на сильную корреляцию между прогнозируемыми и фактическими значениями. Эти результаты предполагают, что модель обладает отличной способностью подгонки в различных обучающих и тестовых наборах, подтверждая, что модель Tent-SSA-BPNN является надежным и стабильным предиктором AWUE.
Таблица 7. Результаты FFCV.
3.2.5. Сравнение производительности моделей
Чтобы дальнейшим образом подтвердить прогностическую эффективность модели Tent-SSA-BPNN, результаты нескольких запусков Tent-SSA-BPNN сравнивались с результатами модели BPNN, модели нейронной сети SSA (SSA-BPNN) и другого широко используемого алгоритма оптимизации, нейронной сети алгоритма серого волка (GWO-BPNN) [87], на наборе данных AWUE в JHP. Точность (ACC), среднеквадратичная ошибка (RMSE) и значения R² для каждой модели после пяти запусков представлены на рисунке 11.
Рисунок 11. Сравнение прогностической производительности четырех моделей.
Анализ рисунка 11 показывает, что диапазон колебаний точности (ACC), среднеквадратичной ошибки (RMSE) и R2 для BPNN относительно велик, что указывает на значительную нестабильность в результатах прогнозирования BPNN для AWUE. Надежность BPNN неадекватна. Напротив, стабильность ACC, RMSE и R2 для NN, оптимизированных одиночными алгоритмами SSA или GWO, значительно выше, чем у BPNN, подчеркивая необходимость алгоритмической оптимизации для BPNN. По сравнению с вышеупомянутыми моделями, производительность модели Tent-SSA-BPNN дальнейшим образом улучшилась, достигнув ACC 95% или выше, RMSE 1,2 или ниже и значения R2 0,99 или выше, значительно превосходя NN, оптимизированные одиночными алгоритмами. Это демонстрирует, что глобальная поисковая способность и точность оптимизации модели Tent-SSA-BPNN были значительно улучшены, позволяя ей точно идентифицировать глобальное оптимальное решение целевой функции, тем самым улучшая эффект оптимизации SSA на производительность NN. Модель Tent-SSA-BPNN характеризуется сильной стабильностью, точностью (ACC) и надежностью, значительно повышая достоверность прогнозирования AWUE и демонстрируя отличную способность в прогнозировании выбросов углерода.
3.2.6. Прогнозирование AWUE в JHP
После проверки модели Tent-SSA-BPNN была спрогнозирована AWUE в JHP, тем самым предоставляя теоретическую основу для формулирования разумной политики AWUE. Тенденции WRPC, SCWS и SAWC прогнозируются на следующие пять лет. Анализируя тенденции этих трех показателей с 2010 по 2022 год, среднегодовые темпы изменения для WRPC, SCWS и SAWC составили 15,57%, 19,57% и 8,55% соответственно. Используя средние темпы изменения, будущие значения для трех показателей были установлены при двух сценариях: непрерывное увеличение и непрерывное уменьшение. Это дает восемь комбинаций трех показателей. Модель Tent-SSA-BPNN использовалась для прогнозирования этих восьми сценариев, с выводами, иллюстрированными на рисунке 12.
Рисунок 12. Прогноз тенденций AWUE в JHP.
Восемь предустановленных сценариев визуально представлены, где «+» указывает на увеличивающийся фактор, «−» указывает на уменьшающийся фактор, и три различных символа обозначают WRPC, SCWS и SAWC. Как иллюстрируется на рисунке 12, когда значения трех показателей — WRPC, SCWS и SAWC — непрерывно увеличиваются или уменьшаются (т.е. «+ + +“ и «− − −»), значение AWUE увеличивается или уменьшается соответственно. Когда SAWC вместе с двумя другими показателями непрерывно увеличивается или уменьшается (т.е. «+ + +» и «− − −»), AWUE соответственно отражает эти изменения. В частности, когда присутствуют «+ + +» и «− − −», AWUE будет демонстрировать тенденцию к увеличению или уменьшению, указывая на положительную корреляцию между значениями трех показателей и AWUE. Сравнивая «+ + +» с «- + +», «+ − +» и «+ + −» и анализируя сценарии, в которых один показатель уменьшается, а другие увеличиваются, очевидно, что когда SAWC непрерывно уменьшается, AWUE имеет тенденцию к уменьшению; когда SCWS непрерывно уменьшается, AWUE остается стабильной; и когда WRPC непрерывно уменьшается, AWUE сначала увеличивается, прежде чем стабилизироваться. Это предполагает, что SAWC положительно влияет на значение AWUE в JHP. Эти результаты указывают на то, что SAWC оказывает наиболее значительное влияние на AWUE, тогда как WRPC оказывает наименьшее влияние на AWUE в JHP. Сравнивая «− − −» с «+ − −» и «− + −» с «− − +», анализируется непрерывное увеличение одного показателя при постоянстве двух других показателей. Когда WRPC непрерывно увеличивается, значение AWUE имеет тенденцию стабилизироваться; когда SAWC непрерывно увеличивается, AWUE сначала стабилизируется, а затем увеличивается; и когда SCWS непрерывно увеличивается, AWUE имеет тенденцию к уменьшению. Этот вывод усиливает вывод о том, что SAWC значительно влияет на AWUE в JHP. Результаты «+ − +» и «+ − −», а также «− +» и «− +», обобщены в следующей таблице, которая сравнивает «+ − +» с «+ − −», «− +» с «+ + −» и «+ + −» с «+ − −». Анализируя различия между сценариями, в которых два показателя снижаются, по сравнению со сценариями, где один показатель снижается, очевидно, что общее значение AWUE уменьшается более значительно, когда два показателя снижаются. Более того, до тех пор, пока SAWC снижалась, общее значение AWUE демонстрировало нисходящую тенденцию. Сравнивая «+ + +» с «− + +», «+ − −» с «+ + +» и «+ − −» с «− − +», чтобы проанализировать эффекты WRPC и SCWS на значения AWUE, когда SCWS увеличивается и WRPC уменьшается, значение AWUE больше, чем когда WRPC увеличивается и SCWS уменьшается, указывая на то, что SCWS оказывает более значительное влияние на AWUE, чем WRPC, что согласуется с выводами, сделанными в предыдущем разделе.
В заключение, степень влияния трех показателей на AWUE в JHP ранжируется следующим образом: SAWC > SCWS > WRPC, причем SAWC оказывает наиболее значительное влияние. Это подчеркивает важность оптимизации управления сельскохозяйственными водными ресурсами, повышения эффективности орошения и минимизации потерь воды. Эффективное управление сельскохозяйственными водными ресурсами не только улучшает сельскохозяйственную производительность, но и положительно влияет на общее устойчивое использование водных ресурсов.
4. Обсуждение
Это исследование было направлено на оценку и прогнозирование AWUE в JHP, решая ключевые исследовательские вопросы, связанные с пространственными и временными вариациями AWUE и производительностью прогностических моделей. Модель SE-SBM использовалась для расчетов AWUE, тогда как улучшенная модель Tent-SSA-BPNN использовалась для прогнозирования тенденций AWUE. Наши результаты предоставляют представление о пространственных диспропорциях в AWUE в разных городах и демонстрируют эффективность модели Tent-SSA-BPNN в повышении точности прогнозирования. Результаты показали небольшую нисходящую тенденцию в AWUE по JHP, со заметными пространственными и временными вариациями, наблюдаемыми среди городов. Эти тенденции предполагают, что в то время как некоторые регионы добиваются прогресса в оптимизации использования воды, другие испытывают стагнацию или спад. Диспропорция между такими городами, как Ухань, и меньшими городами, такими как Цяньцзян, подчеркивает необходимость регионально-специфических стратегий в управлении водными ресурсами и сельскохозяйственных практиках. Оценочные метрики модели прогнозирования Tent-SSA-BPNN превосходят таковые у модели оптимизации одиночным алгоритмом, демонстрируя надежную прогностическую производительность. Анализ прогнозирует, что SAWC оказывает большее влияние на AWUE в JHP, чем WRPC и SCWS.
С теоретической точки зрения, большинство предыдущих исследований было сосредоточено на прогнозировании результатов с помощью традиционных моделей или построения обычных BPNN [88]. Улучшенная модель Tent-SSA-BPNN превосходит традиционные модели благодаря своей уникальной интеграции глобальной оптимизации от SSA и возможностей нелинейного прогнозирования от BPNN. Модель избегает локальных оптимумов, повышая точность прогнозирования. Более того, хаотическое отображение Тента увеличивает разнообразие начальной популяции, предотвращая раннюю сходимость к субоптимальным решениям, что является общей проблемой традиционных методов. Это приводит к более надежным и достоверным прогнозам тенденций AWUE. Улучшенная модель Tent-SSA-BPNN в этом исследовании превосходит традиционные модели благодаря своей способности комбинировать глобальную поисковую способность SSA с захватом нелинейности нейронной сети с обратным распространением ошибки (BPNN). SSA оптимизирует веса и смещения BPNN более эффективно, избегая локальных оптимумов, тем самым улучшая точность прогнозирования. Дополнительно, хаотическое отображение Тента улучшает способность SSA исследовать пространство решений за счет увеличения разнообразия начальной популяции, что дальнейшим образом способствует надежности модели. Более того, сравнение нескольких запусков с моделями BPNN, SSA-BPNN и GWO-BPNN указывает на то, что традиционная BPNN решила свои предыдущие недостатки относительно стабильности. Все оценочные метрики превосходят таковые у моделей, оптимизированных одиночными алгоритмами, демонстрируя, что улучшенный SSA значительно улучшает глобальную поисковую способность и точность оптимизации нейронных сетей, приводя к заметным улучшениям в их производительности. Это подтверждает, что модель Tent-SSA-BPNN демонстрирует сильную стабильность, точность и надежность в качестве прогностической модели для сельскохозяйственных водных ресурсов. Это исследование решает пробел в прогнозировании AWUE и предлагает новые идеи для связанных исследований в этой области. Предыдущие исследования, такие как исследования Wang и др. (2024) и Zhang и др. (2023), сильно полагались на такие методы, как DEA и SFA, для анализа эффективности [89,90]. Хотя эти подходы полезны, они борются с нелинейными отношениями и многомерными наборами данных, ограничивая их прогностическую силу. Напротив, модель Tent-SSA-BPNN, интегрируя алгоритм глобальной оптимизации (SSA) и нелинейную нейронную сеть (BPNN), эффективно решает эти проблемы, предлагая более точный и адаптируемый инструмент для анализа AWUE. Это исследование основывается на предыдущих работах и улучшает их, интегрируя эти передовые методы. Напротив, улучшенная модель Tent-SSA-BPNN, используемая в этом исследовании, успешно преодолевает эти ограничения, интегрируя алгоритм глобального поиска и модель нелинейного прогнозирования, предлагая более точный и надежный инструмент для анализа AWUE. Эти результаты согласуются с последними исследованиями по оптимизации прогностических моделей для AWUE, но они расширяют предыдущую работу, демонстрируя практическую применимость модели Tent-SSA-BPNN в реальных условиях [41]. С практической точки зрения, улучшение AWUE в JHP имеет значительные последствия для управления водными ресурсами и сельскохозяйственной политики. Оптимизируя распределение водных ресурсов, модель Tent-SSA-BPNN может информировать политические решения, направленные на повышение эффективности использования воды в различных регионах. Модель Tent-SSA-BPNN предлагает политикам ключевые идеи для улучшения стратегий распределения водных ресурсов. Эта модель может эффективно определять районы в пределах JHP, где внедрение передовых технологий орошения, таких как капельные или спринклерные системы, даст наиболее значительное сокращение потерь воды. Более того, прогностические возможности модели позволяют политикам стратегически расставлять приоритеты мер по сохранению воды в регионах, сталкивающихся с самым высоким риском нехватки воды, тем самым способствуя более целенаправленному и эффективному распределению ресурсов. Для сельскохозяйственных практиков прогностическая способность модели может помочь в принятии обоснованных решений о выборе культур, методах орошения и распределении ресурсов, в конечном счете улучшая производительность при одновременном снижении потребления воды. Эти результаты подчеркивают роль оптимизации AWUE в обеспечении устойчивого развития сельского хозяйства в вододефицитных регионах.
В свете результатов этого исследования, JHP должна предпринять следующие меры для повышения уровней AWUE. Во-первых, усиление управления и оптимального распределения водных ресурсов имеет ключевое значение. Учитывая значительные различия в AWUE среди городов JHP, обсужденные ранее, рациональное распределение и эффективное управление водными ресурсами должны быть обеспечены путем создания и усиления комплексной системы управления водными ресурсами [91]. Во-вторых, сельскохозяйственная структура посевов должна быть скорректирована на основе климатических и почвенных условий JHP для продвижения водосберегающих и эффективных сельскохозяйственных практик [92]. В-третьих, важно продвигать технологии водосберегающего орошения, такие как капельное и спринклерное орошение, которые могут значительно сократить потери воды.
Хотя это исследование направлено на всесторонний анализ учета и прогнозирования AWUE в JHP, оно неизбежно имеет определенные ограничения. Ограничения следующие:
(1) AWUE значительно изменяется со временем, и исследование может быть ограничено скоростью получения самых последних данных. Это ограничение может помешать результатам полностью отражать текущую ситуацию.
(2) AWUE варьируется среди различных регионов и типов культур, и одна модель может адекватно не представлять характеристики всех сельскохозяйственных регионов JHP, что может повлиять на универсальность прогностических результатов.
(3) JHP охватывает обширную территорию, демонстрируя вариации в условиях водных ресурсов и моделях сельскохозяйственного развития в различных регионах. Следовательно, это исследование может не быть в состоянии охватить все регионы всесторонне, что может ограничить сделанные выводы.
В свете этих ограничений будущие исследования должны отдавать приоритет следующему:
(1) Усилить методы сбора данных и их обработки. Разработан эффективный алгоритм для обработки крупномасштабных данных о сельскохозяйственных водных ресурсах, направленный на улучшение скорости обработки и точности при минимизации влияния ошибок данных на результаты исследования.
(2) Это исследование направлено на изучение краткосрочного и долгосрочного воздействия стихийных бедствий, таких как наводнения и засухи, на AWUE и предложение соответствующих стратегий и планов реагирования.
(3) Интегрировать факторы изменения климата, включая осадки и температуру, в модель, чтобы проанализировать их влияние на AWUE и повысить адаптивность прогнозов в будущем.
5. Выводы
В условиях растущей нехватки воды и необходимости устойчивости сельского хозяйства, улучшение AWUE имеет ключевое значение для обеспечения устойчивого управления водными ресурсами и продовольственной безопасности. Это исследование сосредоточено на JHP и AWUE, используя модель SE-SBM для оценки и улучшенную модель Tent-SSA-BPNN для прогнозирования. Новая интеграция хаотического отображения Тента с SSA и BPNN значительно улучшает точность и надежность прогнозов AWUE. Предоставляя более надежный инструмент прогнозирования, это исследование решает ключевые проблемы в управлении водными ресурсами и устойчивости сельского хозяйства в вододефицитных регионах. Результаты указывают на то, что AWUE в JHP показала небольшую нисходящую тенденцию с 2010 по 2022 год, со значительными пространственными и временными диспропорциями по регионам. Использование модели Tent-SSA-BPNN позволило точно смоделировать эти вариации, улучшив понимание того, как экологические и сельскохозяйственные факторы взаимодействуют, формируя эффективность использования воды. Модель Tent-SSA-BPNN достигла впечатляющей точности прогнозирования 96,218% (ACC) и RMSE 0,952, превзойдя традиционные модели и подтвердив свою надежную производительность в прогнозировании AWUE. Результаты представлены ниже.
(1) С 2010 по 2022 год AWUE в JHP демонстрировала небольшую нисходящую тенденцию. Значения AWUE в JHP ранжируются от самого высокого до самого низкого следующим образом: Ичан > Сяогань > Цзинмэнь > Ухань > Цзинчжоу > Цяньцзян > Сяньтао > Тяньмэнь.
(2) В этом разделе обсуждаются характеристики пространственного распределения и динамические тенденции изменения AWUE в JHP. Общая тенденция указывает на то, что центр тяжести AWUE мигрировал на восток и юг. SDE указывает, что AWUE в JHP первоначально демонстрировала рост агломерации; однако с 2012 года она начала оптимизироваться, что привело к снижению степени агломерации. Направление распределения оставалось относительно стабильным, преимущественно вдоль оси «северо-восток–юго-запад». Распределение имеет более равномерную эллиптическую форму. MI иллюстрирует динамическую тенденцию пространственной корреляции в JHP, с высокими положительными значениями в 2012 и 2016 годах, означающими сильную пространственную агрегацию, тогда как отрицательные значения в 2020 году предполагают пространственную дисперсию.
(3) WRPC, SCWS и SAWC были выбраны в качестве прогностических переменных для прогнозирования AWUE JHP. FFCV использовалась для оценки результатов прогнозирования. Результаты указали, что ACC и RMSE, прогнозируемые моделью Tent-SSA-BPNN, составили 96,218% и 0,952 соответственно. Значение R2 составило 0,9939, демонстрируя высокую точность и подгонку результатов прогнозирования модели.
(4) Результаты нескольких оценок модели Tent-SSA-BPNN, наряду с моделями BPNN, SSA-BPNN и GWO-BPNN, были сравнены. Результаты указывают на то, что ACC модели Tent-SSA-BPNN остается стабильной на уровне примерно 96%, тогда как RMSE остается ниже 1,2. Значение R2 постоянно превышает 0,99, решая недостатки стабильности традиционной BPNN. Все оценочные метрики превосходят таковые у моделей оптимизации одиночным алгоритмом, демонстрируя, что улучшенный SSA значительно улучшает глобальную поисковую способность и точность оптимизации BPNN, таким образом положительно влияя на оптимизацию производительности нейронных сетей. Модель Tent-SSA-BPNN служит моделью прогнозирования сельскохозяйственных выбросов углерода, характеризующейся сильной стабильностью, точностью и надежностью.
(5) Интегрируя WRPC, SCWS и SAWC, модель Tent-SSA-BPNN использовалась для прогнозирования AWUE JHP на следующие пять лет. Результаты указали на то, что три показателя положительно коррелировали с AWUE, с их влиянием, ранжированным следующим образом, от наибольшего к наименьшему: SAWC > SCWS > WRPC. Более того, SAWC имеет доминирующее влияние на AWUE, указывая на то, что управление SAWC может эффективно регулировать AWUE.
(6) Модель Tent-SSA-BPNN представляет собой значительный прогресс в прогнозировании AWUE за счет интеграции хаотического отображения Тента и SSA с BPNN. По сравнению с традиционными методами, это нововведение позволяет проводить более точные прогнозы и обеспечивает надежную производительность. Ее потенциальные применения выходят за пределы JHP, предлагая ценную информацию для устойчивого сельского хозяйства в вододефицитных регионах по всему миру. Модель также может быть адаптирована для прогнозирования AWUE в других отраслях, способствуя более широким стратегиям управления водными ресурсами.
(7) Результаты этого исследования подчеркивают критическую важность для политиков и сельскохозяйственных заинтересованных сторон интегрировать эти идеи в свои стратегии управления водными ресурсами и сельскохозяйственные методологии. Модель Tent-SSA-BPNN представляет надежную основу, которая улучшает возможности прогнозирования AWUE и оптимизирует распределение воды, тем самым предлагая масштабируемый подход к решению проблем нехватки воды и содействию устойчивому сельскохозяйственному развитию. Более того, исследователи должны продолжать совершенствовать и тестировать модель Tent-SSA-BPNN в разных регионах и контекстах, продвигая ее применимость и внося вклад в глобальные усилия по обеспечению устойчивости воды и продовольственной безопасности.
Ссылки
1. Chowdhury, S.; Al-Zahrani, M. Characterizing Water Resources and Trends of Sector Wise Water Consumptions in Saudi Arabia. J. King Saud Univ.-Eng. Sci. 2015, 27, 68–82. [Google Scholar] [CrossRef]
2. Zehtabiyan-Rezaie, N.; Alvandifar, N.; Saffaraval, F.; Makkiabadi, M.; Rahmati, N.; Saffar-Avval, M. A Solar-Powered Solution for Water Shortage Problem in Arid and Semi-Arid Regions in Coastal Countries. Sustain. Energy Technol. Assess. 2019, 35, 1–11. [Google Scholar] [CrossRef]
3. Feng, X.; Fu, B.; Piao, S.; Wang, S.; Ciais, P.; Zeng, Z.; Lü, Y.; Zeng, Y.; Li, Y.; Jiang, X.; et al. Revegetation in China’s Loess Plateau Is Approaching Sustainable Water Resource Limits. Nat. Clim. Chang. 2016, 6, 1019–1022. [Google Scholar] [CrossRef]
4. Adhikari, R.; Bristow, K.L.; Casey, P.S.; Freischmidt, G.; Hornbuckle, J.W.; Adhikari, B. Preformed and Sprayable Polymeric Mulch Film to Improve Agricultural Water Use Efficiency. Agric. Water Manag. 2016, 169, 1–13. [Google Scholar] [CrossRef]
5. Keenan, T.F.; Hollinger, D.Y.; Bohrer, G.; Dragoni, D.; Munger, J.W.; Schmid, H.P.; Richardson, A.D. Increase in Forest Water-Use Efficiency as Atmospheric Carbon Dioxide Concentrations Rise. Nature 2013, 499, 324–327. [Google Scholar] [CrossRef]
6. Zhao, G.; Dou, Y. Research on the Utilization Efficiency of Agricultural Water Resources in Tianjin Based on DEA Model. In Proceedings of the 5th Annual International Conference on Social Science and Contemporary Humanity Development (SSCHD 2019), Wuhan, China, 15–16 November 2019; Jang, S.J., Zhu, Z., Eds.; Atlantis Press: Paris, France, 2019; Volume 376, pp. 556–560. [Google Scholar]
7. Mu, L.; Fang, L.; Wang, H.; Chen, L.; Yang, Y.; Qu, X.J.; Wang, C.Y.; Yuan, Y.; Wang, S.B.; Wang, Y.N. Exploring Northwest China’s Agricultural Water-Saving Strategy: Analysis of Water Use Efficiency Based on an SE-DEA Model Conducted in Xi’an, Shaanxi Province. Water Sci. Technol. 2016, 74, 1106–1115. [Google Scholar] [CrossRef]
8. Ren, C.; Li, R.; Guo, P. Two-Stage DEA Analysis of Water Resource Use Efficiency. Sustainability 2017, 9, 52. [Google Scholar] [CrossRef]
9. Yang, S.; Wang, H.; Tong, J.; Ma, J.; Zhang, F.; Wu, S. Technical Efficiency of China’s Agriculture and Output Elasticity of Factors Based on Water Resources Utilization. Water 2020, 12, 2691. [Google Scholar] [CrossRef]
10. Wang, G.; Chen, J.; Zhou, Q.; Chu, X.; Zhou, X. Modelling Analysis of Water-Use Efficiency of Maize in Heihe River Basin. Phys. Chem. Earth 2016, 96, 50–54. [Google Scholar] [CrossRef]
11. Chang, K.-Y.; Riley, W.J.; Keenan, T.F. Hourly Water-Carbon Interactions Modulate Decadal Water-Use Efficiency Trends Inferred from Ecosystem-Scale Measurements. Agric. For. Meteorol. 2022, 326, 109158. [Google Scholar] [CrossRef]
12. Tuoku, L.; Men, B. Evaluation of Water Resource Use Efficiency in Beijing-Tianjin-Hebei Based on Three-Dimensional Water Ecological Footprint. Ecol. Indic. 2023, 154, 110884. [Google Scholar] [CrossRef]
13. Riera, F.S.; Bruemmer, B. Environmental Efficiency of Wine Grape Production in Mendoza, Argentina. Agric. Water Manag. 2022, 262, 107376. [Google Scholar] [CrossRef]
14. Zhi, Y.; Zhang, F.; Wang, H.; Qin, T.; Tong, J.; Wang, T.; Wang, Z.; Kang, J.; Fang, Z. Agricultural Water Use Efficiency: Is There Any Spatial Correlation between Different Regions? Land 2022, 11, 77. [Google Scholar] [CrossRef]
15. Veettil, P.C.; Speelman, S.; van Huylenbroeck, G. Estimating the Impact of Water Pricing on Water Use Efficiency in Semi-Arid Cropping System: An Application of Probabilistically Constrained Nonparametric Efficiency Analysis. Water Resour. Manag. 2013, 27, 55–73. [Google Scholar] [CrossRef]
16. Feng, D.; Ning, S.; Zhang, J.; Zhu, H.; Tang, J.; Sun, X.; Xu, Y. Agricultural Use of Deserted Saline Land through an Optimized Drip Irrigation System with Mild Salinized Water. Agric. Water Manag. 2023, 281, 108261. [Google Scholar] [CrossRef]
17. Mardani, A.; Zavadskas, E.K.; Streimikiene, D.; Jusoh, A.; Khoshnoudi, M. A Comprehensive Review of Data Envelopment Analysis (DEA) Approach in Energy Efficiency. Renew. Sustain. Energy Rev. 2017, 70, 1298–1322. [Google Scholar] [CrossRef]
18. Kuosmanen, T.; Saastamoinen, A.; Sipiläinen, T. What Is the Best Practice for Benchmark Regulation of Electricity Distribution? Comparison of DEA, SFA and StoNED Methods. Energy Policy 2013, 61, 740–750. [Google Scholar] [CrossRef]
19. Zhang, Y.; Xu, X. Study on Regional Carbon Emission Efficiency Based on SE-SBM and Geographic Detector Models. Environ. Dev. Sustain. 2023, 24, 3619–3639. [Google Scholar] [CrossRef]
20. Zhang, D.; Shen, J.; Sun, F. Water Resources Liability Measurement and the Driving Factors of Water Resources Liability Intensity. Water Resour. Manag. 2022, 36, 1553–1569. [Google Scholar] [CrossRef]
21. Meng, L.-S. Compound Synthesis or Growth and Development of Roots/Stomata Regulate Plant Drought Tolerance or Water Use Efficiency/Water Uptake Efficiency. J. Agric. Food Chem. 2018, 66, 3595–3604. [Google Scholar] [CrossRef]
22. Bakhsh, A.; Hussein, F.; Ahmad, N.; Hassan, A.; Farid, H.U. Modeling Deficit Irrigation Effects on Maize to Improve Water Use Efficiency. Pak. J. Agric. Sci. 2012, 49, 365–374. [Google Scholar]
23. Yang, G.; Fan, Z.; Li, D.; Feng, S.; Liu, G.; Li, Q.; Dong, Z. Prediction of Water Resource Carrying Status Based on the “three Red Lines” Water Resource Management Policy in the Coastal Area of Jiangsu Province, China. Water Policy 2022, 24, 1610–1630. [Google Scholar] [CrossRef]
24. Wang, S.; Wang, L. Grey Model and Linear Regression Approaches to Agricultural Water Consumption Forecasting in the Shiyang River Basin. In Proceedings of the 2010 International Conference on Engineering Computation (ICEC 2010), Valencia, Spain, 24–26 October 2010; Yang, P., Ed.; London Science Publishing Ltd.: London, UK, 2010; pp. 39–44. [Google Scholar]
25. Yang, G.; Yang, Y.; Gong, G.; Chen, X. The Coupling and Coordination Characteristics of Agricultural Green Water Resources and Agricultural Economic Development in China. Environ. Dev. Sustain. 2024, 26, 2131–2151. [Google Scholar] [CrossRef]
26. Ju, Z.; Li, D.; Cui, Y.; Sun, D. Optimizing the Water and Nitrogen Management Scheme to Enhance Potato Yield and Water-Nitrogen Use Efficiency. Agronomy 2024, 14, 1651. [Google Scholar] [CrossRef]
27. Traore, A.; Ata-Ul-Karim, S.T.; Duan, A.; Soothar, M.K.; Traore, S.; Zhao, B. Predicting Equivalent Water Thickness in Wheat Using UAV Mounted Multispectral Sensor through Deep Learning Techniques. Remote Sens. 2021, 13, 4476. [Google Scholar] [CrossRef]
28. Boschetti, F.; Grigg, N.J.; Enting, I. Modelling = Conditional Prediction. Ecol. Complex. 2011, 8, 86–91. [Google Scholar] [CrossRef]
29. Hui, P.; Qu, W.; Tang, J.; Chen, J. Traffic Indexes Prediction Based on Grey Prediction Model. In Proceedings of the 2013 Sixth International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 28–29 October 2013; IEEE: New York, NY, USA, 2013; Volume 1, pp. 244–247. [Google Scholar]
30. Liu, D.; Chen, X.; Nakato, T. Resilience Assessment of Water Resources System. Water Resour. Manag. 2012, 26, 3743–3755. [Google Scholar] [CrossRef]
31. Duncan, K.; Komendantskaya, E.; Stewart, R.; Lones, M. Relative Robustness of Quantized Neural Networks Against Adversarial Attacks. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; IEEE: New York, NY, USA, 2020. [Google Scholar]
32. Yang, L.; Zhou, L. A Novel BP Neural Network for Forecasting Agriculture Water Consumption. In Proceedings of the International Conference on Graphic and Image Processing (ICGIP 2011), Cairo, Egypt, 1–3 October 2011; Xie, Y., Zheng, Y., Eds.; Spie-Int Soc Optical Engineering: Bellingham, WA, USA, 2011; Volume 8285, p. 828579. [Google Scholar]
33. Ma, N. Analysis of Industry Convergence Based on Improved Neural Network. Soft Comput. 2022, 26, 7437–7448. [Google Scholar] [CrossRef]
34. Zhu, Y.; Dong, Z.; Cheng, Z.; Huang, X.; Dong, Y.; Zhang, Z. Neural Network Extended State-Observer for Energy System Monitoring. Energy 2023, 263, 125736. [Google Scholar] [CrossRef]
35. Ye, G.; Lin, T. Channel Capacity of Neural Networks. In Proceedings of the Artificial Neural Networks and Machine Learning—ICANN 2021, Bratislava, Slovakia, 14–17 September 2021; Part IV. Farkas, I., Masulli, P., Otte, S., Wermter, S., Eds.; Springer International Publishing Ag: Cham, Switzerland, 2021; Volume 12894, pp. 253–265. [Google Scholar]
36. Watanabe, C.; Hiramatsu, K.; Kashino, K. Modular Representation of Layered Neural Networks. Neural Netw. 2018, 97, 62–73. [Google Scholar] [CrossRef]
37. Tong, L.; Qin, L.; Xie, C.; Liu, H.; Wang, Y.; Guan, C.; Huang, S. Distribution of Antibiotics in Alluvial Sediment near Animal Breeding Areas at the Jianghan Plain, Central China. Chemosphere 2017, 186, 100–107. [Google Scholar] [CrossRef]
38. Hou, J.; Styles, D.; Cao, Y.; Ye, X. The Sustainability of Rice-Crayfish Coculture Systems: A Mini Review of Evidence from Jianghan Plain in China. J. Sci. Food Agric. 2021, 101, 3843–3853. [Google Scholar] [CrossRef] [PubMed]
39. Ren, W.; Zhang, X.; Peng, H. Evaluation of Temporal and Spatial Changes in Ecological Environmental Quality on Jianghan Plain From 1990 to 2021. Front. Environ. Sci. 2022, 10, 884440. [Google Scholar] [CrossRef]
40. Wallace, J.S. Increasing Agricultural Water Use Efficiency to Meet Future Food Production. Agric. Ecosyst. Environ. 2000, 82, 105–119. [Google Scholar] [CrossRef]
41. Wang, F.; Yu, C.; Xiong, L.; Chang, Y. How Can Agricultural Water Use Efficiency Be Promoted in China? A Spatial-Temporal Analysis. Resour. Conserv. Recycl. 2019, 145, 411–418. [Google Scholar] [CrossRef]
42. Xu, H.; Yang, R.; Song, J. Agricultural Water Use Efficiency and Rebound Effect: A Study for China. Int. J. Environ. Res. Public Health 2021, 18, 7151. [Google Scholar] [CrossRef]
43. Zhao, H.; Li, D.; Han, Z.; Wang, H.; Duan, Y. Spatial-Temporal Evolution and Convergence Analysis of Urban Environmental Efficiency in China’s Coastal Areas Based on Undesirable Output. Pol. J. Environ. Stud. 2024, 33, 5485–5495. [Google Scholar] [CrossRef]
44. Guan, N.; Liu, L.; Dong, K.; Xie, M.; Du, Y. Agricultural Mechanization, Large-Scale Operation and Agricultural Carbon Emissions. Cogent Food Agric. 2023, 9, 2238430. [Google Scholar] [CrossRef]
45. Li, S.; Wang, Z. The Effects of Agricultural Technology Progress on Agricultural Carbon Emission and Carbon Sink in China. Agriculture 2023, 13, 793. [Google Scholar] [CrossRef]
46. Ding, X.; Zhang, Z.; Wu, F.; Xu, X. Study on the Evolution of Water Resource Utilization Efficiency in Tibet Autonomous Region and Four Provinces in Tibetan Areas under Double Control Action. Sustainability 2019, 11, 3396. [Google Scholar] [CrossRef]
47. Zheng, H.; Zhang, J.; Zhao, X.; Mu, H. Exploring the Affecting Mechanism between Environmental Regulation and Economic Efficiency: New Evidence from China’s Coastal Areas. Ocean Coast. Manag. 2020, 189, 105148. [Google Scholar] [CrossRef]
48. Fan, J.; Li, Y.; Wang, T. An Improved African Vultures Optimization Algorithm Based on Tent Chaotic Mapping and Time-Varying Mechanism. PLoS ONE 2021, 16, e0260725. [Google Scholar] [CrossRef] [PubMed]
49. Akraam, M.; Rashid, T.; Zafar, S. An Image Encryption Scheme Proposed by Modifying Chaotic Tent Map Using Fuzzy Numbers. Multimed. Tools Appl. 2023, 82, 16861–16879. [Google Scholar] [CrossRef]
50. Lin, Q.; Yang, S.; Yang, R.; Wu, H. Transistor Modeling Based on LM-BPNN and CG-BPNN for the GaAs pHEMT. Int. J. Numer. Model. Electron. Netw. Devices Fields 2024, 37, e3268. [Google Scholar] [CrossRef]
51. Zhou, H.; Yu, K.-M. Quality Prediction in Manufacturing Process Using a PCA-BPNN Model. In Fuzzy Systems and Data Mining II; Sun, S., TallonBallesteros, A.J., Pamucar, D.S., Liu, F., Eds.; Ios Press: Amsterdam, The Netherlands, 2016; Volume 293, pp. 390–396. [Google Scholar]
52. Abd Al-Hameeda, K.A. Spearman’s Correlation Coefficient in Statistical Analysis. Int. J. Nonlinear Anal. Appl. 2022, 13, 3249–3255. [Google Scholar] [CrossRef]
53. Lu, W.; Sarkar, A.; Hou, M.; Liu, W.; Guo, X.; Zhao, K.; Zhao, M. The Impacts of Urbanization to Improve Agriculture Water Use Efficiency—An Empirical Analysis Based on Spatial Perspective of Panel Data of 30 Provinces of China. Land 2022, 11, 80. [Google Scholar] [CrossRef]
54. Song, H.Y.; Park, S. An Analysis of Correlation between Personality and Visiting Place Using Spearman’s Rank Correlation Coefficient. KSII Trans. Internet Inf. Syst. 2020, 14, 1951–1966. [Google Scholar] [CrossRef]
55. Chan, J.Y.-L.; Leow, S.M.H.; Bea, K.T.; Cheng, W.K.; Phoong, S.W.; Hong, Z.-W.; Chen, Y.-L. Mitigating the Multicollinearity Problem and Its Machine Learning Approach: A Review. Mathematics 2022, 10, 1283. [Google Scholar] [CrossRef]
56. Salmeron-Gomez, R.; Garcia-Garcia, C.B.; Garcia-Perez, J. A Redefined Variance Inflation Factor: Overcoming the Limitations of the Variance Inflation Factor. Comput. Econ. 2024, 52, 11–37. [Google Scholar] [CrossRef]
57. Cheng, J.; Sun, J.; Yao, K.; Xu, M.; Cao, Y. A Variable Selection Method Based on Mutual Information and Variance Inflation Factor. Spectrochim. Acta Part A-Mol. Biomol. Spectrosc. 2022, 268, 120652. [Google Scholar] [CrossRef]
58. Wang, L.; Zhu, Y. Neural-Network-Based Nonlinear Model Predictive Control of Multiscale Crystallization Process. Processes 2022, 10, 2374. [Google Scholar] [CrossRef]
59. Moon, Y.S.; Ali, S. Possible Mechanisms for the Equilibrium of ACC and Role of ACC Deaminase-Producing Bacteria. Appl. Microbiol. Biotechnol. 2022, 106, 877–887. [Google Scholar] [CrossRef] [PubMed]
60. Willmott, C.J.; Matsuura, K. Advantages of the Mean Absolute Error (MAE) over the Root Mean Square Error (RMSE) in Assessing Average Model Performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
61. Renaud, O.; Victoria-Feser, M.-P. A Robust Coefficient of Determination for Regression. J. Stat. Plan. Inference 2010, 140, 1852–1862. [Google Scholar] [CrossRef]
62. Yadav, S.; Shukla, S. Analysis of K-Fold Cross-Validation over Hold-Out Validation on Colossal Datasets for Quality Classification. In Proceedings of the 2016 IEEE 6th International Conference on Advanced Computing (IACC), Bhimavaram, India, 27–28 February 2016; pp. 78–83. [Google Scholar]
63. Zhang, X.; Liu, C.-A. Model Averaging Prediction by K-Fold Cross-Validation. J. Econom. 2023, 235, 280–301. [Google Scholar] [CrossRef]
64. Wang, J.; Shi, P.; Jiang, P.; Hu, J.; Qu, S.; Chen, X.; Chen, Y.; Dai, Y.; Xiao, Z. Application of BP Neural Network Algorithm in Traditional Hydrological Model for Flood Forecasting. Water 2017, 9, 48. [Google Scholar] [CrossRef]
65. Răducanu, M.; Cheroiu, D.-G.; Nițu, C.M. A Novel Comparison between Different Composite Chaotic Maps Applied on Sound Encryption. In Proceedings of the 2023 46th International Conference on Telecommunications and Signal Processing (TSP), Prague, Czech Republic, 12–14 July 2023; pp. 225–229. [Google Scholar]
66. Nardo, L.; Nepomuceno, E.; Muñoz, D.; Butusov, D.; Arias-Garcia, J. A Hardware-Efficient Perturbation Method to the Digital Tent Map. Electronics 2023, 12, 1953. [Google Scholar] [CrossRef]
67. Ormerod, J.T.; Wand, M.P. Gaussian Variational Approximate Inference for Generalized Linear Mixed Models. J. Comput. Graph. Stat. 2012, 21, 2–17. [Google Scholar] [CrossRef]
68. Meng, Q.; Pi, H.; Nie, Y.; Ma, J. Research on the Coupling and Coordinated Development of Guangxi’s Tourism Industry, New Urbanization and Environmental Health System in the Post-Epidemic Era. Front. Public Health 2024, 12, 1331765. [Google Scholar] [CrossRef]
69. Burer, S.; Piccialli, V. Three Methods for Robust Grading. Eur. J. Oper. Res. 2019, 272, 364–371. [Google Scholar] [CrossRef]
70. Gan, R.; Zhang, L.; Yang, Y.; Wang, E.; Woodgate, W.; Zhang, Y.; Haverd, V.; Kong, D.; Fischer, T.; Chiew, F.; et al. Estimating Ecosystem Maximum Light Use Efficiency Based on the Water Use Efficiency Principle. Environ. Res. Lett. 2021, 16, 104032. [Google Scholar] [CrossRef]
71. Pan, Z.; Wang, Y.; Zhou, Y.; Wang, Y. Analysis of the Water Use Efficiency Using Super-Efficiency Data Envelopment Analysis. Appl. Water Sci. 2020, 10, 139. [Google Scholar] [CrossRef]
72. Liu, H.; Xia, J.; Zou, L.; Huo, R. Comprehensive Quantitative Evaluation of the Water Resource Carrying Capacity in Wuhan City Based on the “Human–Water–City” Framework: Past, Present and Future. J. Clean. Prod. 2022, 366, 132847. [Google Scholar] [CrossRef]
73. Yang, J.; Wang, X.; Li, X.; Tian, Z.; Zou, G.; Du, L.; Guo, X. Potential Risk Identification of Agricultural Nonpoint Source Pollution: A Case Study of Yichang City, Hubei Province. Sustainability 2023, 15, 16324. [Google Scholar] [CrossRef]
74. Qian, L.; Chen, C.; Chen, X.; Zeng, W.; Gao, Y.; Deng, K. Cotton Flooding and Drought Analysis Regarding Growth Stages in Hubei, China, Using a Daily Agrometeorological Index. Int. J. Agric. Biol. Eng. 2023, 16, 173–183. [Google Scholar] [CrossRef]
75. Pan, F.; Shu, N.; Wan, Q.; Huang, Q.; Wang, L. Identifying the Spatial Structure and Influence Mechanism of Characteristic Protection Villages under the Background of Rural Revitalization: A Case Study of Hubei Province, China. Authorea 2023, 57, 1105–1122. [Google Scholar] [CrossRef]
76. Wang, X.; Peng, W.; Xiong, H. Spatial-Temporal Evolution and Driving Factors of Rural Resilience in the Urban Agglomerations in the Middle Reaches of the Yangtze River, China. Environ. Sci. Pollut. Res. 2024, 31, 25076–25095. [Google Scholar] [CrossRef]
77. Li, X.; Yu, B.; Cui, J.; Zhu, Y. Building a New Framework for Evaluating the Livability of Living Space on the Basis of the Daily Activities of Rural Residents: A Case Study of Jianghan Plain. Int. J. Environ. Res. Public Health 2022, 19, 10615. [Google Scholar] [CrossRef]
78. Huang, J.; Song, L.; Yu, M.; Zhang, C.; Li, S.; Li, Z.; Geng, J.; Zhang, C. Quantitative Spatial Analysis of Thermal Infrared Radiation Temperature Fields by the Standard Deviational Ellipse Method for the Uniaxial Loading of Sandstone. Infrared Phys. Technol. 2022, 123, 104150. [Google Scholar] [CrossRef]
79. Zhao, Y.; Wu, Q.; Wei, P.; Zhao, H.; Zhang, X.; Pang, C. Explore the Mitigation Mechanism of Urban Thermal Environment by Integrating Geographic Detector and Standard Deviation Ellipse (SDE). Remote Sens. 2022, 14, 3411. [Google Scholar] [CrossRef]
80. Balsa-Barreiro, J.; Li, Y.; Morales, A.; Pentland, A. “Sandy” Globalization and the Shifting Centers of Gravity of World’s Human Dynamics: Implications for Sustainability. J. Clean. Prod. 2019, 239, 117923. [Google Scholar] [CrossRef]
81. Felipe, J.; Kumar, U. The Role of Trade Facilitation in Central Asia. East. Eur. Econ. 2012, 50, 5–20. [Google Scholar] [CrossRef]
82. Zhang, C.; Luo, L.; Xu, W.; Ledwith, V. Use of Local Moran’s I and GIS to Identify Pollution Hotspots of Pb in Urban Soils of Galway, Ireland. Sci. Total Environ. 2008, 398, 212–221. [Google Scholar] [CrossRef]
83. Myers, L.; Sirois, M.J. Spearman Correlation Coefficients, Differences Between. In Wiley StatsRef: Statistics Reference Online; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014; ISBN 978-1-118-44511-2. [Google Scholar]
84. O’brien, R.M. A Caution Regarding Rules of Thumb for Variance Inflation Factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
85. Song, S.; Xiong, X.; Wu, X.; Xue, Z. Modeling the SOFC by BP Neural Network Algorithm. Int. J. Hydrogen Energy 2021, 46, 20065–20077. [Google Scholar] [CrossRef]
86. Cui, K.; Jing, X. Research on Prediction Model of Geotechnical Parameters Based on BP Neural Network. Neural Comput. Appl. 2019, 31, 8205–8215. [Google Scholar] [CrossRef]
87. Liang, Q.; Zhang, X.; Liu, X.; Li, Y. Prediction of High-Temperature Flow Stress of HMn64–8–5–1.5 Manganese Brass Alloy Based on Modified Zerilli-Armstrong, Arrhenius and GWO-BPNN Model. Mater. Res. Express 2022, 9, 096506. [Google Scholar] [CrossRef]
88. Ahmed, A.A.; Sayed, S.; Abdoulhalik, A.; Moutari, S.; Oyedele, L. Applications of Machine Learning to Water Resources Management: A Review of Present Status and Future Opportunities. J. Clean. Prod. 2024, 441, 140715. [Google Scholar] [CrossRef]
89. Wang, R.; Duan, Y. Dynamic Comparison on the Technical Efficiency between China’s EPEs and PEs: Two-Dimensional Measurement Based on SFA. J. Clean. Prod. 2023, 406, 136986. [Google Scholar] [CrossRef]
90. Zhang, W.; Wu, X.; Chen, J. Low-Carbon Efficiency Analysis of Rail-Water Multimodal Transport Based on Cross Efficiency Network DEA Approach. Energy 2024, 305, 132348. [Google Scholar] [CrossRef]
91. Wang, X.; Liu, L.; Zhang, S.; Gao, C. Dynamic Simulation and Comprehensive Evaluation of the Water Resources Carrying Capacity in Guangzhou City, China. Ecol. Indic. 2022, 135, 108528. [Google Scholar] [CrossRef]
92. Krishnan, S.R.; Nallakaruppan, M.K.; Chengoden, R.; Koppu, S.; Iyapparaja, M.; Sadhasivam, J.; Sethuraman, S. Smart Water Resource Management Using Artificial Intelligence—A Review. Sustainability 2022, 14, 13384. [Google Scholar] [CrossRef]
Shao T, Xu X, Su Y. Evaluation and Prediction of Agricultural Water Use Efficiency in the Jianghan Plain Based on the Tent-SSA-BPNN Model. Agriculture. 2025; 15(2):140. https://doi.org/10.3390/agriculture15020140
Перевод статьи «Evaluation and Prediction of Agricultural Water Use Efficiency in the Jianghan Plain Based on the Tent-SSA-BPNN Model» авторов Shao T, Xu X, Su Y., оригинал доступен по ссылке. Лицензия: CC BY. Изменения: переведено на русский язык
Фото: Центральнокитайский сельскохозяйственный университет в Ухане — типичный ландшафт Цзянханьскай равнины, преобразованный урбанизацией/wikipedia
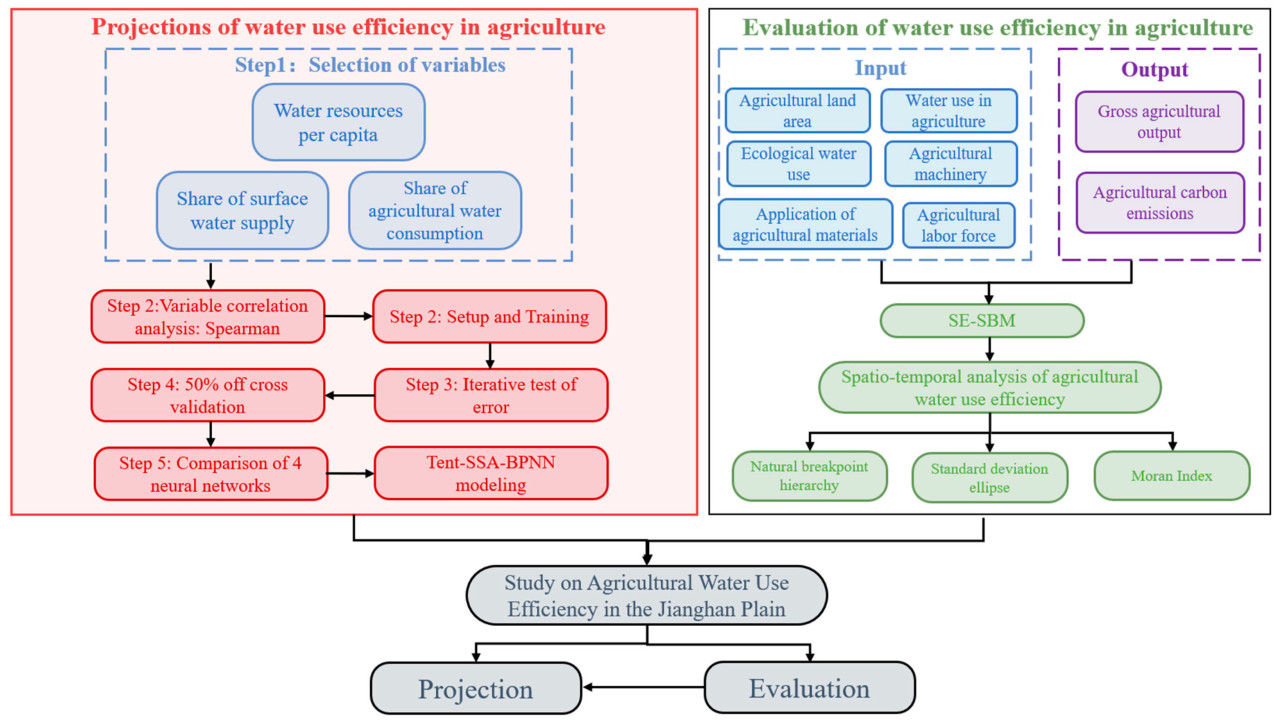
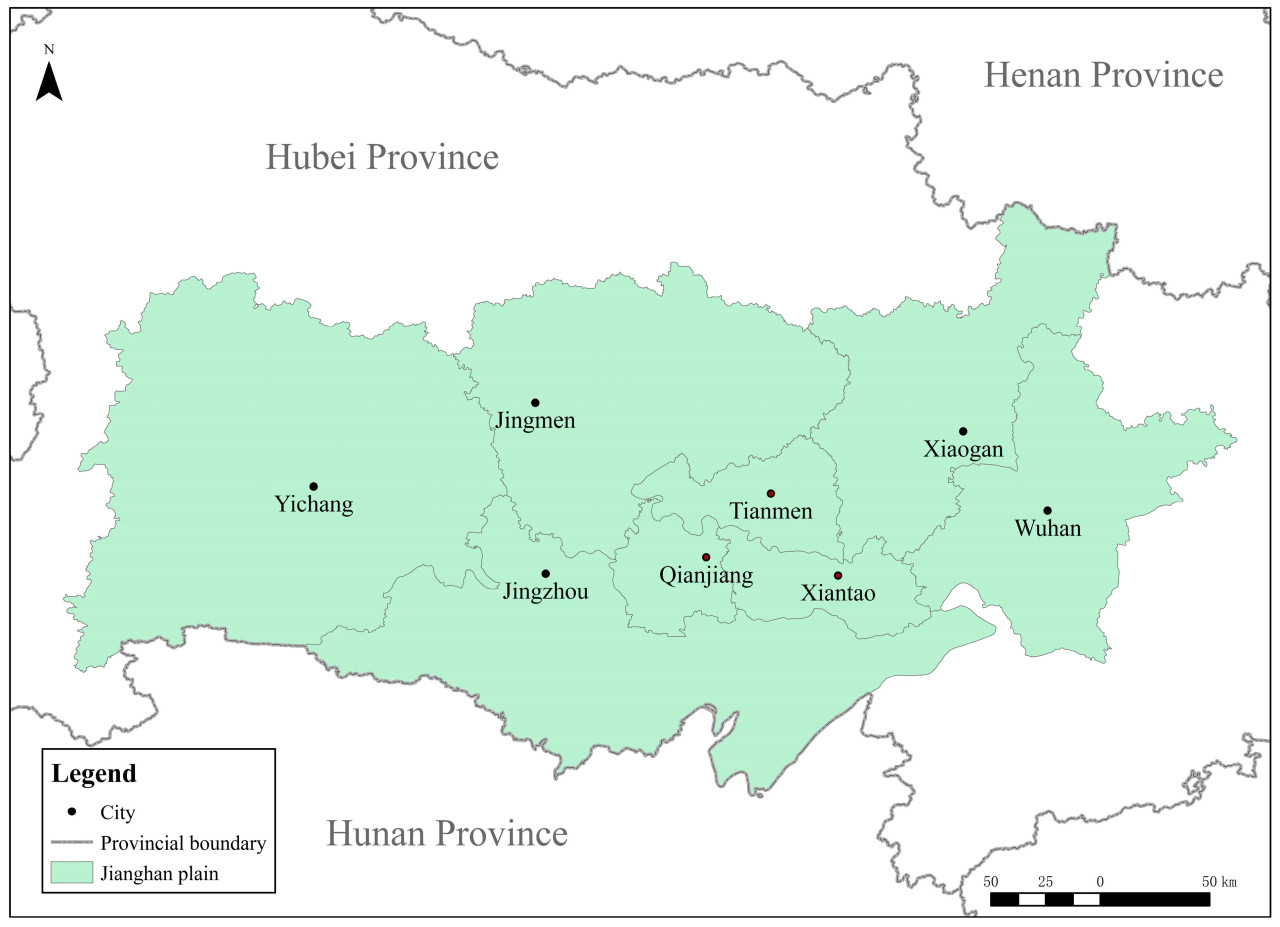
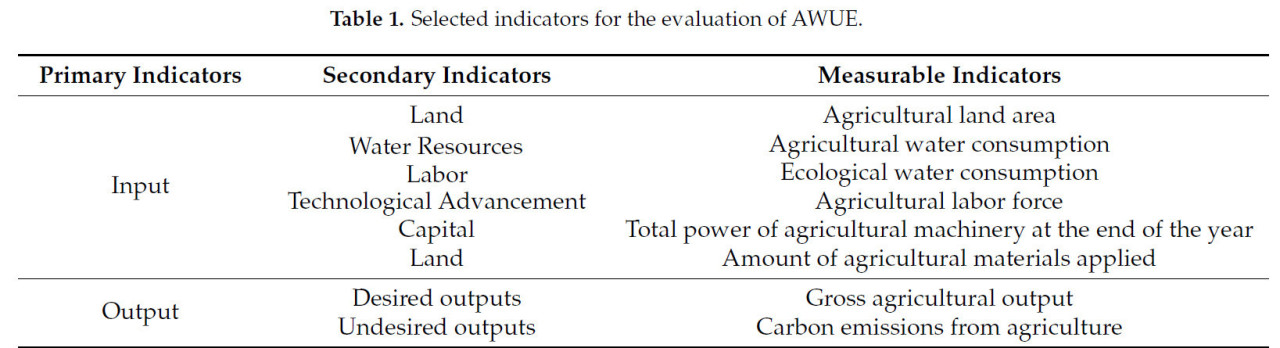
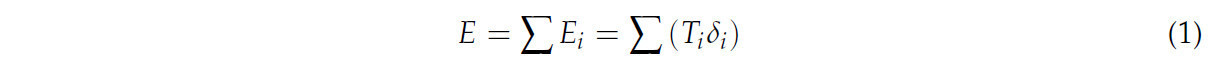
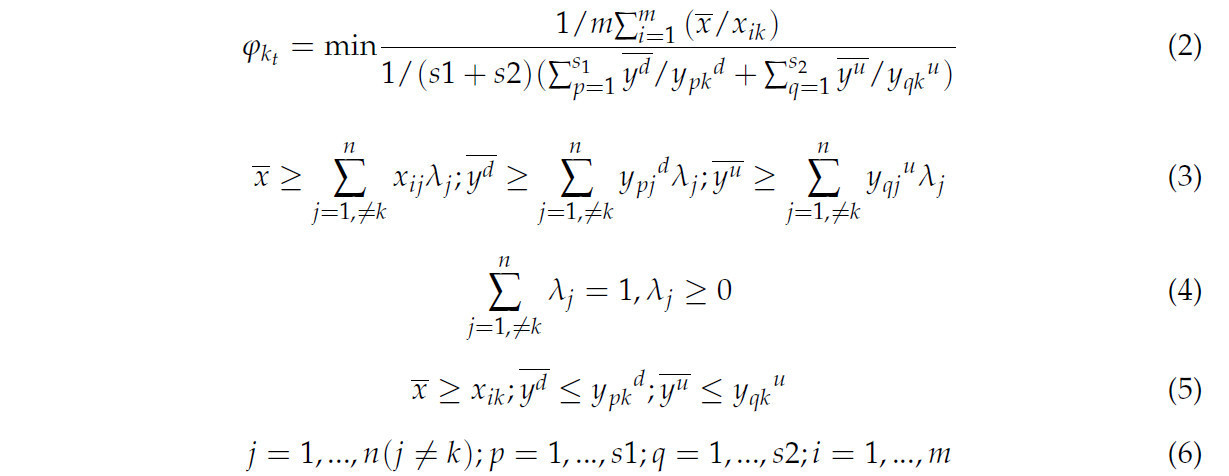
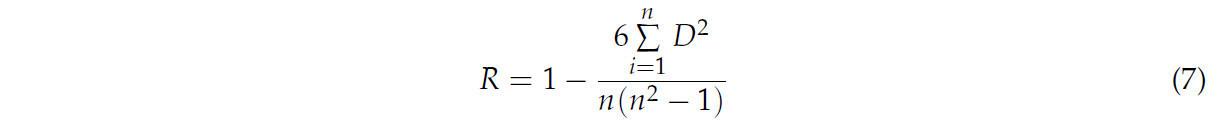
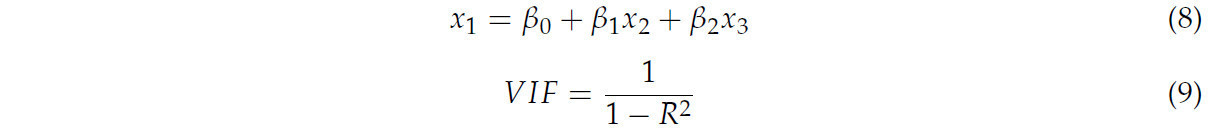
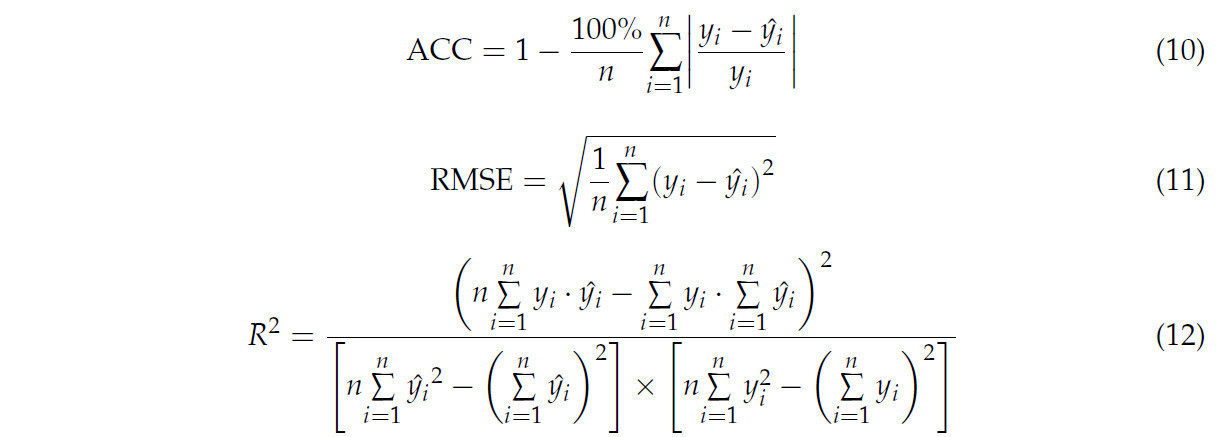
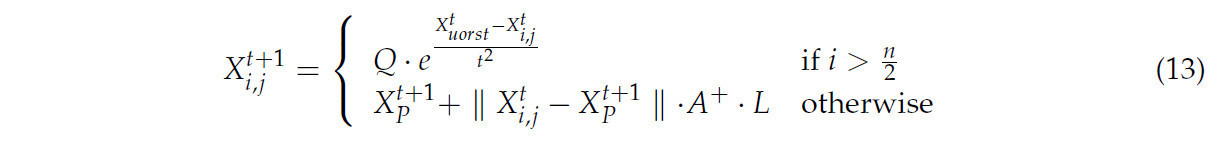
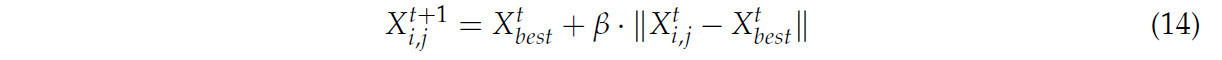
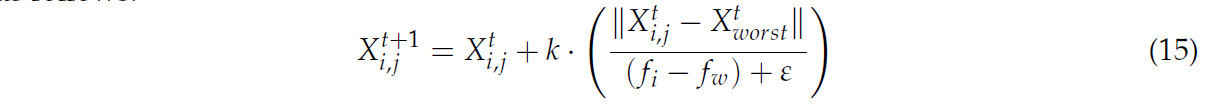
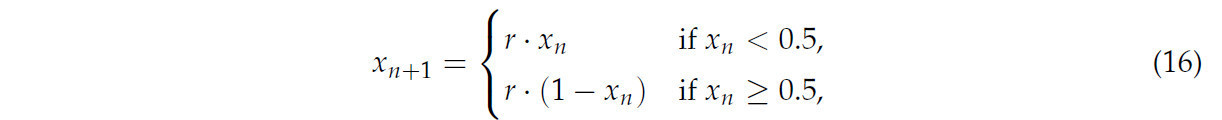
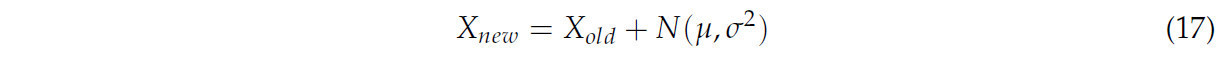
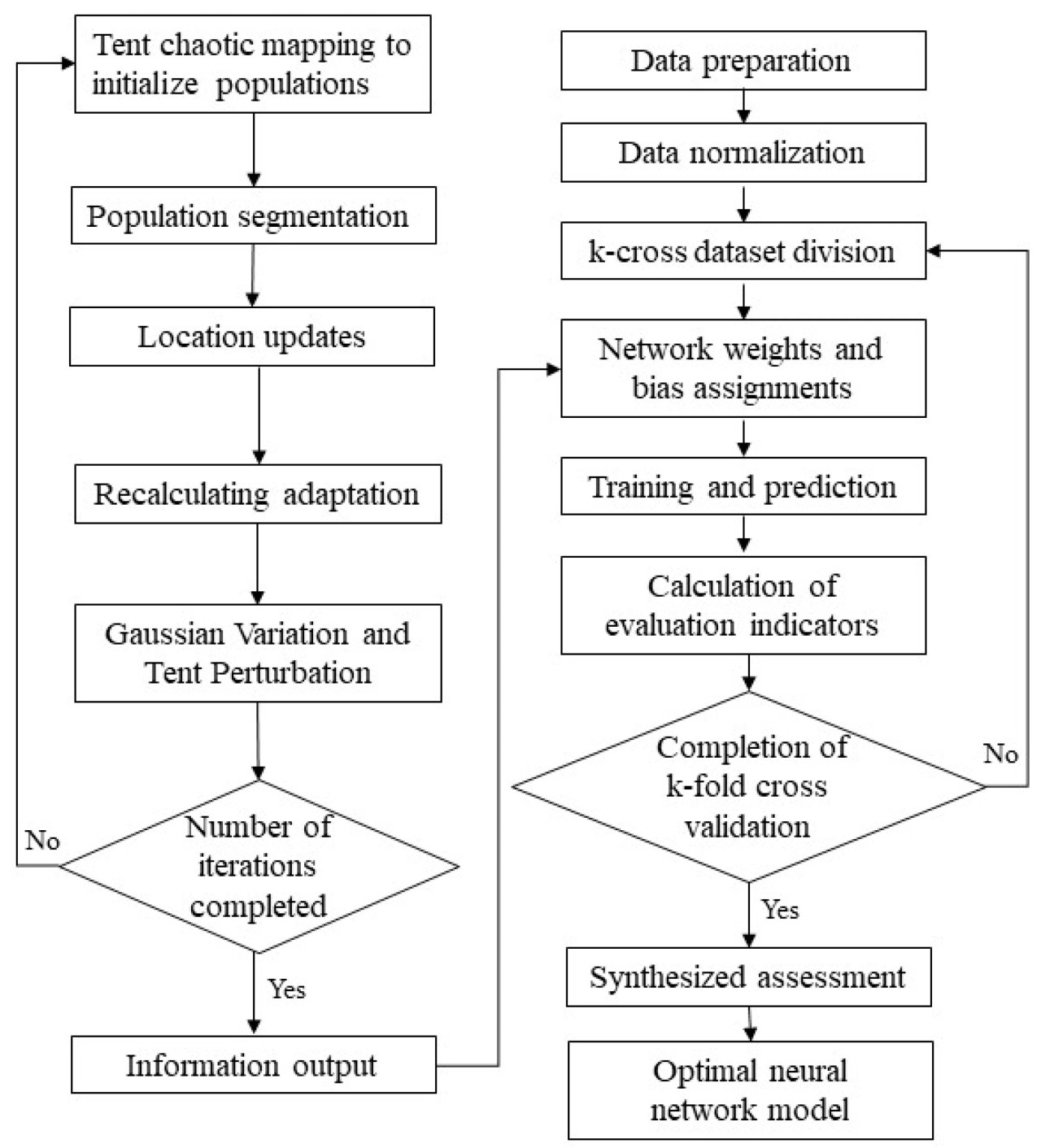
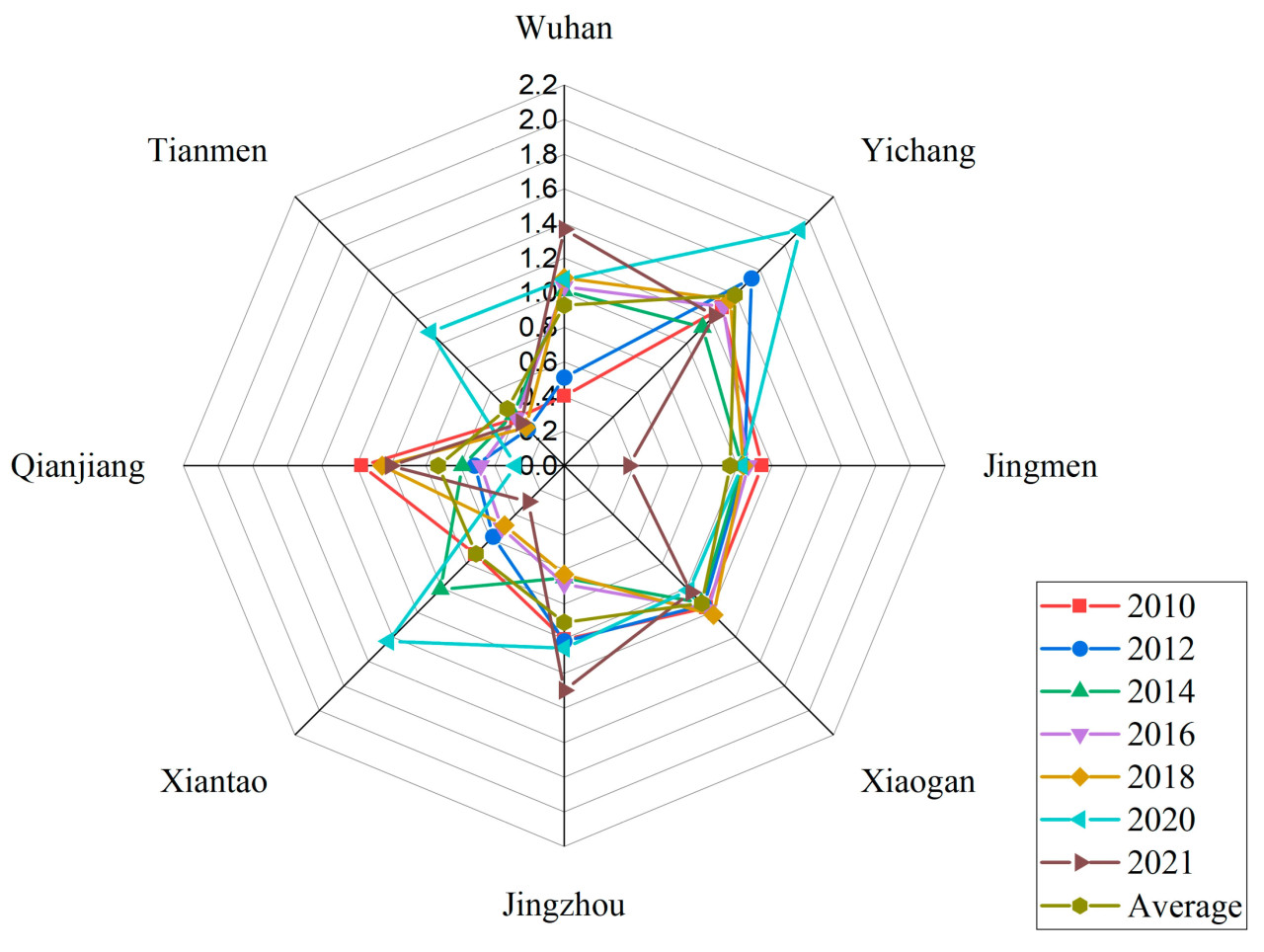
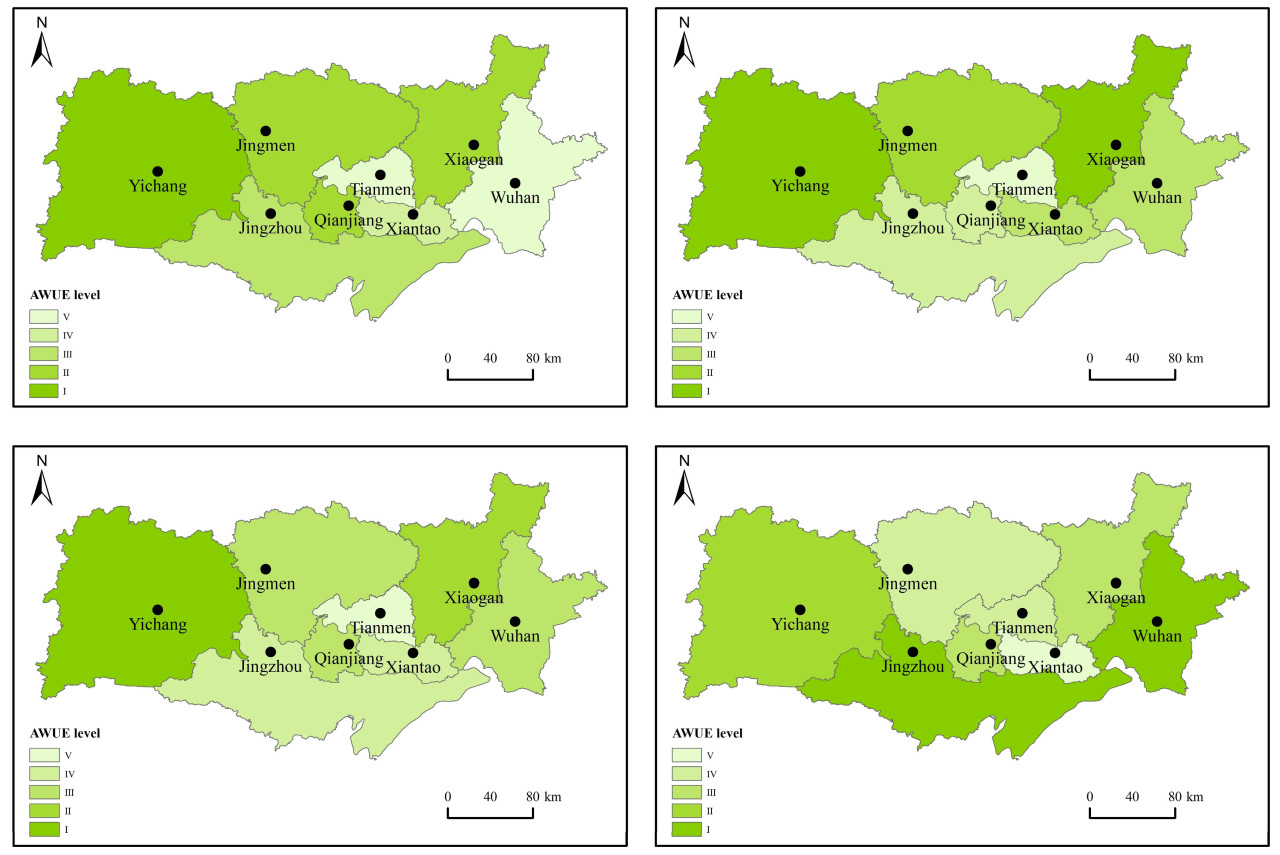
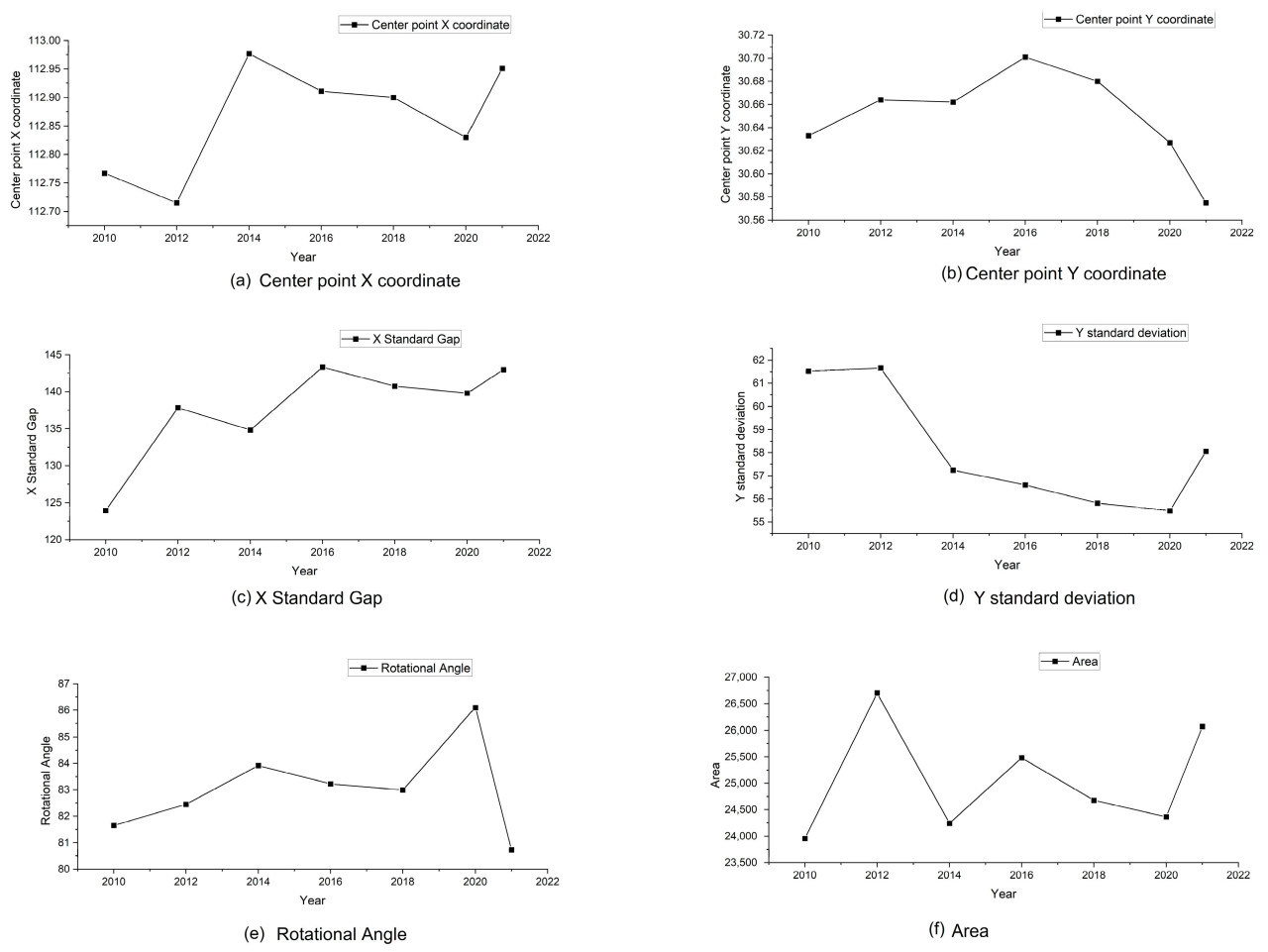
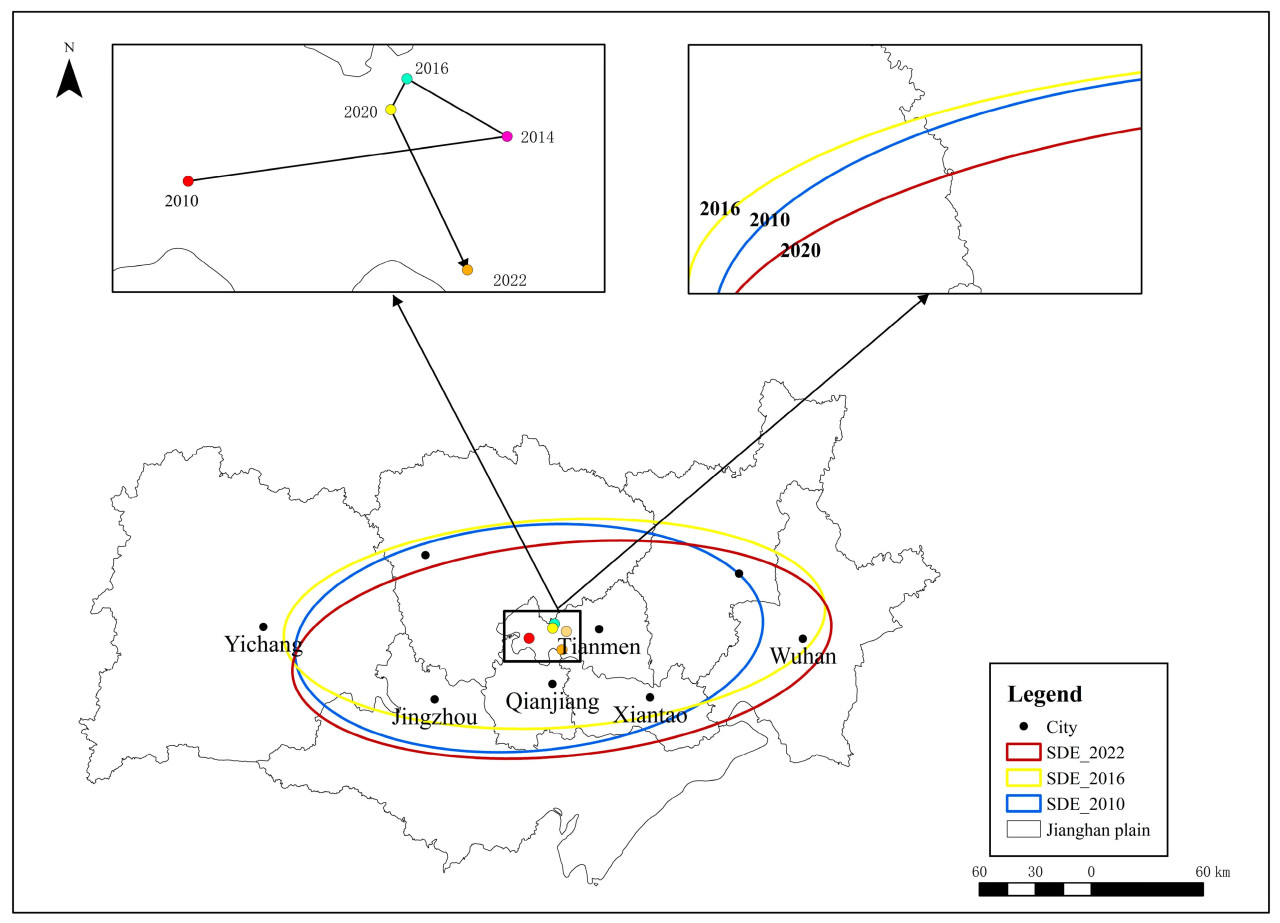

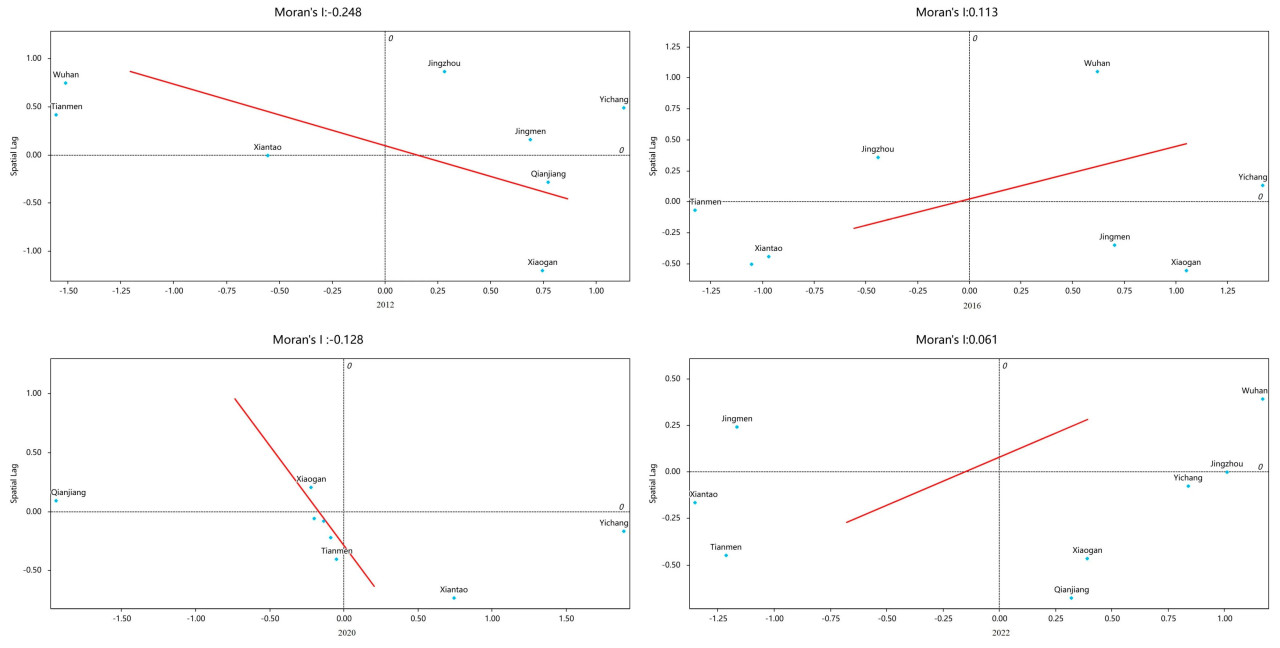



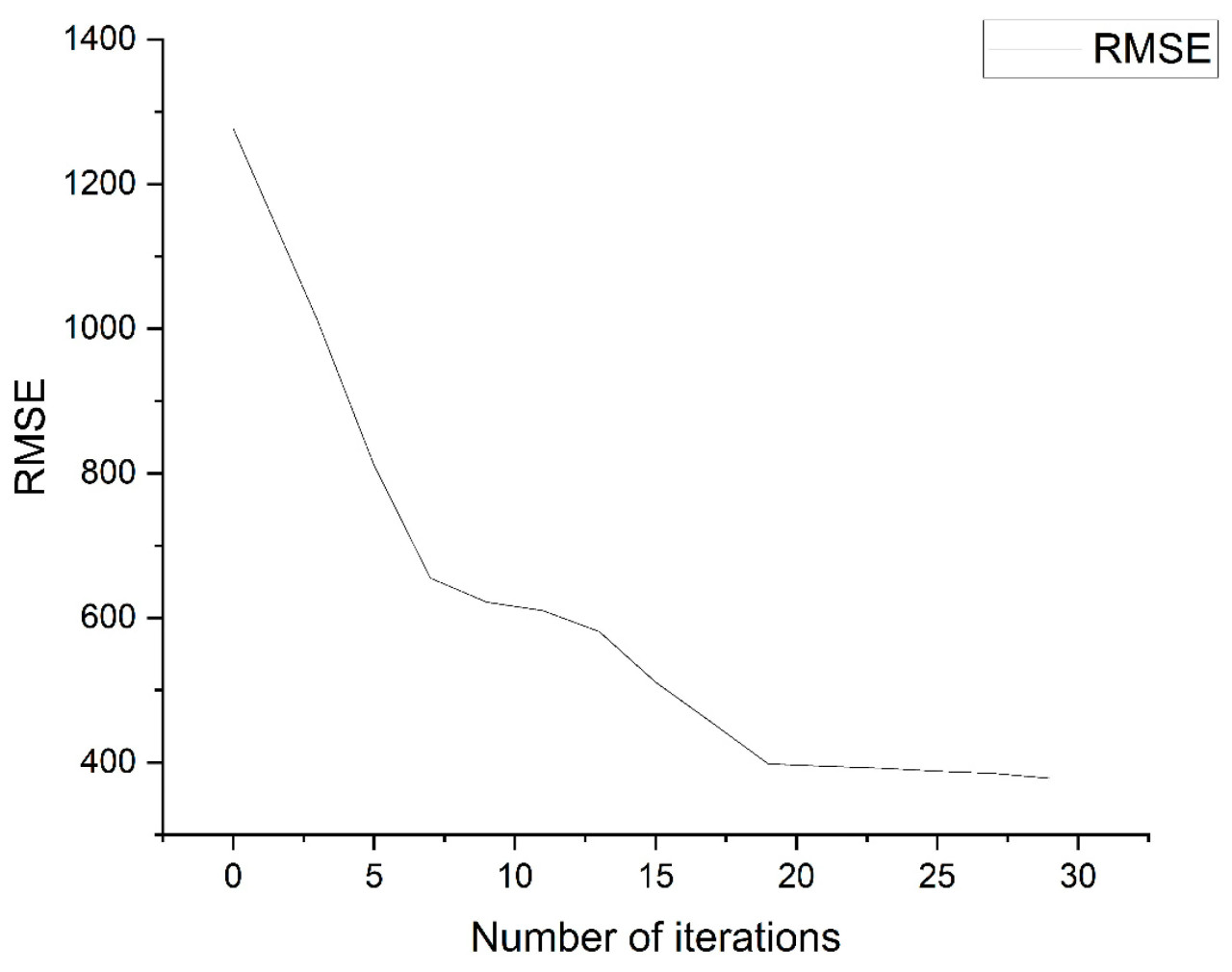
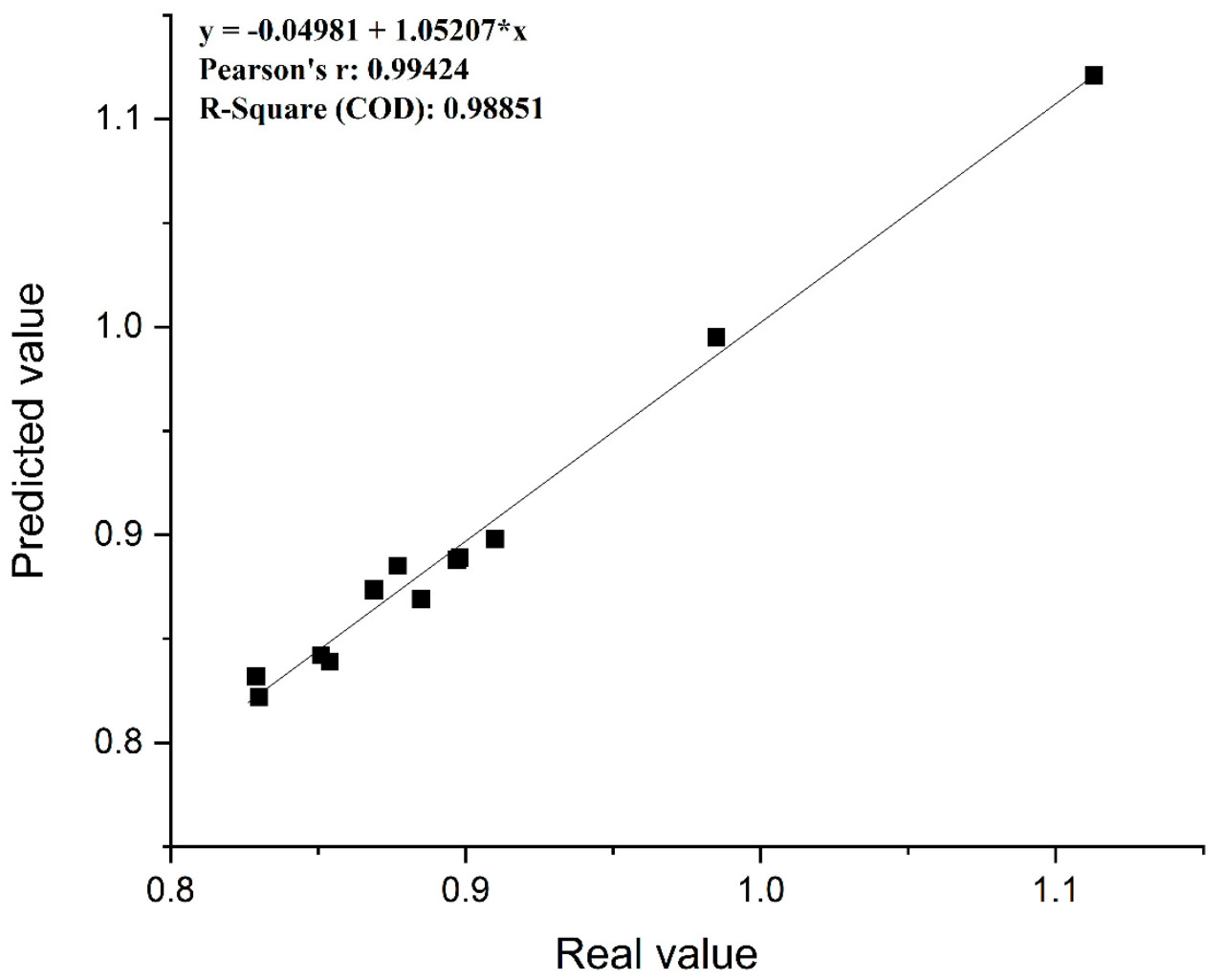
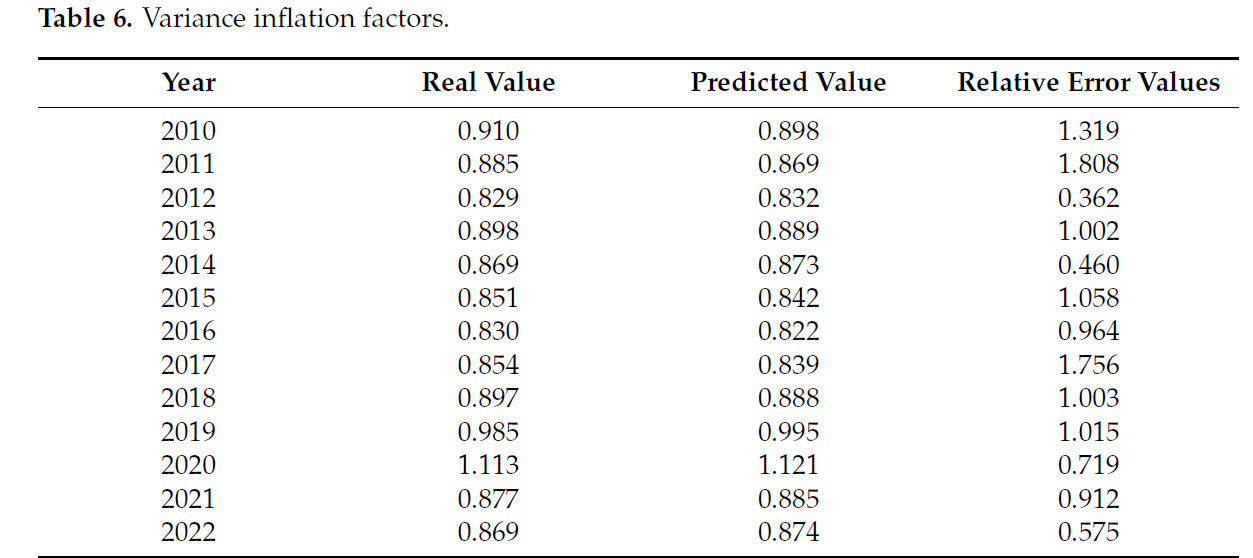
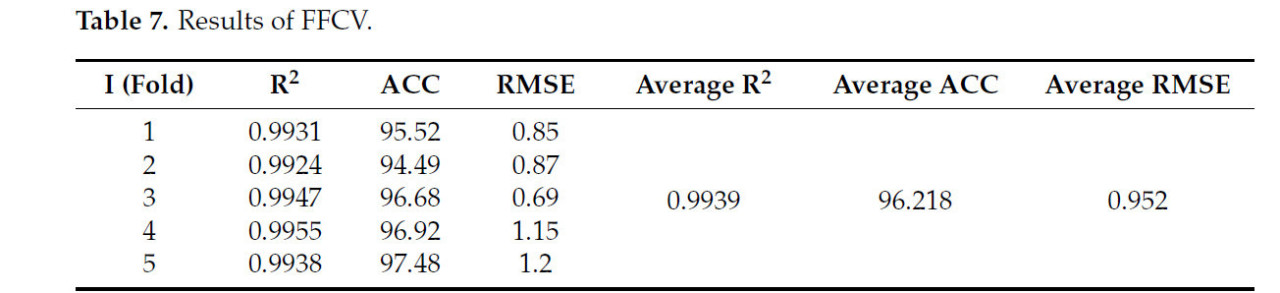
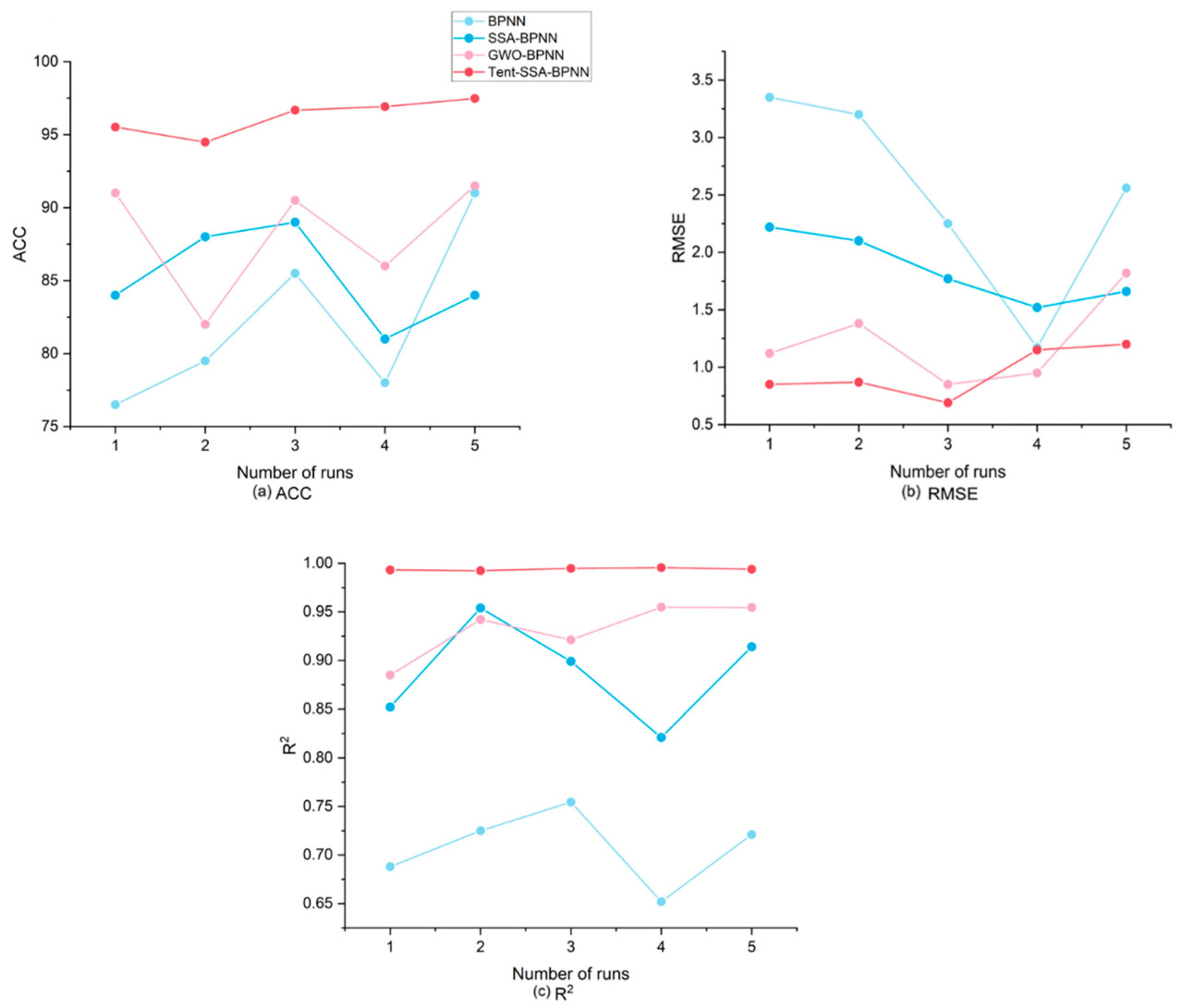
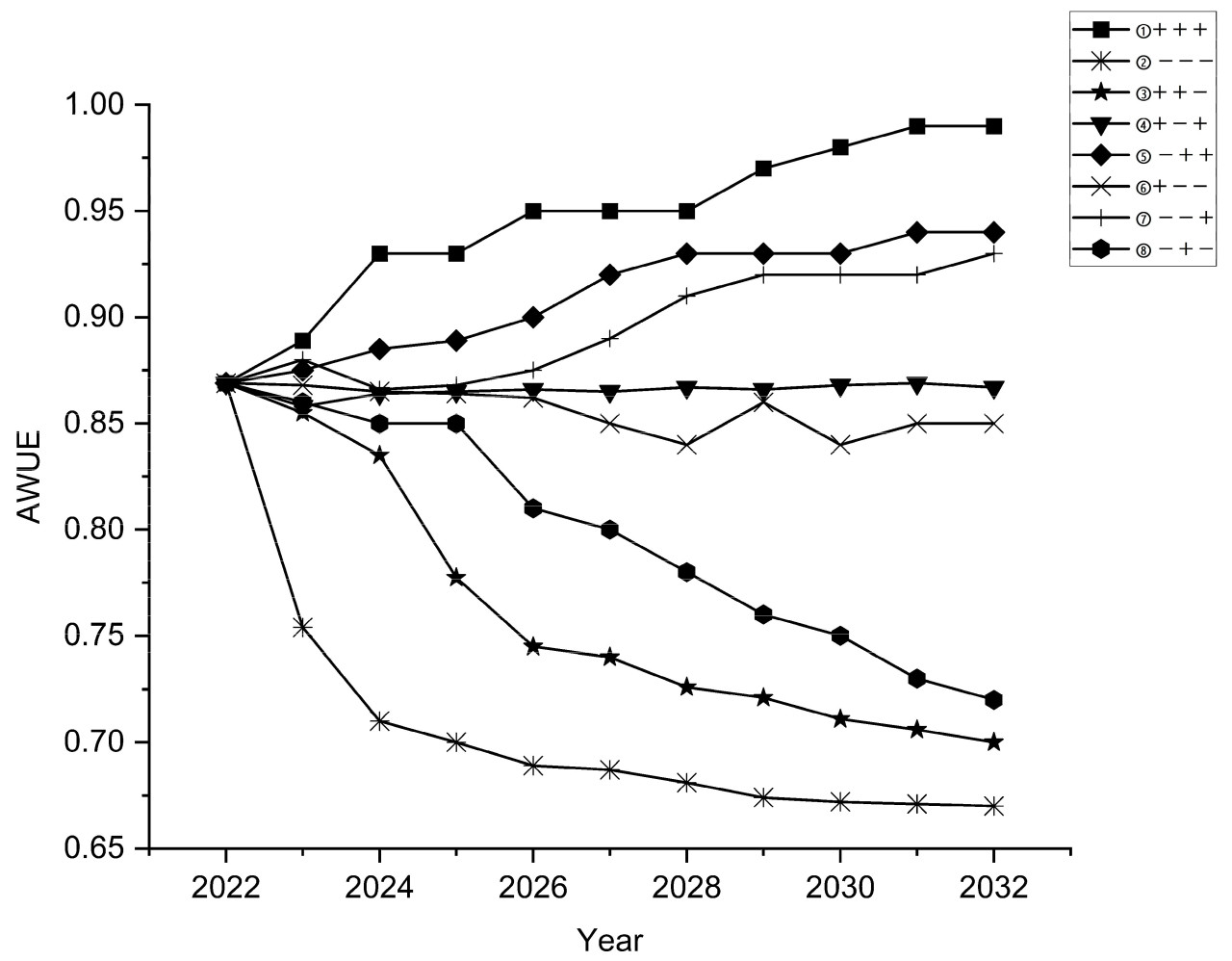






























































































Комментарии (0)