Выгоднее и надежнее: новая система страхования для ферм
Сельскохозяйственное страхование является на сегодняшний день самым популярным инструментом управления рисками в Иране. Несмотря на многолетний опыт, действующая страховая политика Ирана не смогла обеспечить защиту всех производителей в данном секторе. Основной принцип комплексного (общефермерского) страхования заключается в объединении всех страхуемых рисков хозяйства в единый полис и преодолении большинства серьезных недостатков существующих страховых программ. Цель данного исследования — оценить преимущества комплексного страхования (WFI) в провинции Зенджан в Иране.
Аннотация
В исследовании использовались исторические данные на уровне отдельных хозяйств и округов за период с 1982 по 2021 год для оценки функций плотности распределения урожайности и цен, а также для прогнозирования будущих значений. Для расчета ожидаемых компенсаций фермерам, а также гарантированных и смоделированных доходов применялись параметрический и непараметрический подходы. Ставки страховых премий были затем рассчитаны с использованием симуляции PQH и разложения Холецкого и сравнены в трех сценариях: страхование одной, двух и трех культур. Наконец, выгоды для благосостояния фермеров были сравнены в рамках этих трех сценариев со случаем отсутствия страхования.
Результаты показывают, что по сравнению со страхованием урожайности и страхованием отдельных культур, WFI обеспечивает более низкие коэффициенты убыточности. Более того, благосостояние производителей может быть улучшено при страховании хотя бы одной культуры по сравнению с отсутствием страхования. Например, выгоды в виде снижения затрат для производителей при уровне покрытия 75% от страхования пшеницы, ячменя, люцерны, комбинаций пшеница-ячмень, пшеница-люцерна, ячмень-люцерна и пшеница-ячмень-люцерна составляют 8.8, 1.8, 2.9, 1.2, 0.9 и 1.8 соответственно.
Таким образом, мы рекомендуем Иранскому Фонду сельскохозяйственного страхования принять WFI в качестве нового инструмента управления рисками. Данная политика обладает потенциалом для снижения страховых премий и административных издержек при одновременном повышении эквивалентов определенности и выгод для фермеров за счет страхования урожая.
1. Введение
Действующая политика сельскохозяйственного страхования в Иране сталкивается со многими проблемами из-за асимметричной информации. Асимметричная информация приводит к таким проблемам, как неблагоприятный отбор и моральный риск — две глубоко укоренившиеся проблемы в развитии страхования урожая, вызванные скрытой информацией и непредсказуемостью поведения застрахованных фермеров [1]. Моральный риск — это изменение в использовании ресурсов, отклоняющееся от социально оптимального уровня; он возникает, потому что застрахованное лицо может предпринимать действия, влияющие на вероятность убытка, без ведома страховщика. Неблагоприятный отбор происходит, когда из-за асимметричной информации фермеры с более высоким риском убытков с большей вероятностью страхуют свои культуры, чем население в целом [2], что устанавливает среднюю премию всех страховщиков для всех фермеров. Со временем фермеры с низким риском перестанут страховаться, и наоборот, потому что премия высока относительно риска. Хотя эти две проблемы вредят всем страховым рынкам, их воздействие значительно более заметно для сельскохозяйственного сектора, поскольку фермы географически разбросаны, а сбор информации, наблюдение за поведением и диагностика причин становятся более сложными. Дополнительно, снижение уровня покрытия для решения проблемы морального риска уменьшает число людей, покупающих страховку. Из-за этих проблем частное сельскохозяйственное страхование не получило широкого распространения. Высокие административные затраты являются другой проблемой в текущей системе сельскохозяйственного страхования Ирана. Также, хотя спектр услуг, предоставляемых Фондом сельскохозяйственного страхования, расширился в последние годы, он остается далеко ниже установленных целевых показателей. Например, за последние 20 лет застрахованная площадь увеличилась с 2,9 млн до 3,5 млн гектаров для полевых культур и с 92 000 до 690 000 для садоводческой продукции [3]. В то же время количество контрактов с бенефициарами увеличилось с 715 000 до более 1,51 млн, страховые премии выросли с 287 млрд иранских риалов до 1314,3 млрд иранских риалов, а выплаченная фермерам компенсация увеличилась с 484 млрд до 1528,2 млд иранских риалов [3].
В провинции Зенджан внедрение сельскохозяйственного страхования остается низким среди фермеров, с значительными колебаниями в количестве застрахованных фермеров и культур. Пик пришелся на сельскохозяйственный год 2010–2011, после чего последовал постепенный спад. На протяжении последних двух десятилетий фермеры получали больше компенсаций, чем платили страховых премий [3]. Следовательно, коэффициент убыточности в большинстве лет превышал 1, что указывает на неэффективность традиционной системы страхования ферм и необходимость перехода к новым страховым программам. Чтобы устранить пробелы в управлении сельскохозяйственными рисками, были предложены различные политики, включая комплексное (общефермерское) страхование (WFI). Основной исследовательский вопрос заключается в том, можно ли внедрить WFI в сельскохозяйственном секторе провинции Зенджан. В этом исследовании мы сосредоточились на провинции Зенджан как на объекте пилотного исследования, потому что нам были необходимы исторические данные об урожайности культур, особенно на уровне фермы для конкретных фермеров, чтобы оценить функции плотности распределения урожайности и цен. Эти данные были доступны только в этой провинции. WFI представляет особый интерес по нескольким причинам: оно лучше отражает риск на уровне фермы, страхуя от потери валового дохода; оно может более точно оценивать системы органического земледелия с интегрированными программами по нескольким культурам и животноводству; и оно специально нацелено на производителей нескольких, в настоящее время не страхуемых культур [4]. Это исследование было направлено на разработку политики WFI для сельскохозяйственных культур провинции Зенджан и оценку ее влияния на благосостояние фермеров по сравнению с существующими программами. Доход фермеров, зависящий от цен на культуры и урожайности, снижается, когда один фактор падает, а другой остается постоянным. Из-за корреляции между ценами на культуры и урожайностью в регионе, их совместные распределения должны учитываться при оценке риска дохода фермеров. WFI предоставляет более комплексное покрытие, чем другие страховые полисы, за счет решения проблем рисков цен и урожайности, их взаимосвязей и дохода от культур. В этой программе страховщик и страхователь договариваются о случайных переменных, при этом компенсация выплачивается, когда доход падает ниже ожиданий. WFI покрывает несколько культур по более низкой премии, чем программы по одной культуре, страхуя совокупный доход фермы, а не доход от отдельных культур [5]. Zhu и др. [6] сообщают, что премии по WFI на 36% ниже, чем при страховании отдельных культур. Hennessy и др. [7] утверждают, что WFI является более рентабельным, чем другие контракты при том же ожидаемом доходе, причем ставка дисконта увеличивается по мере уменьшения корреляции между продуктами. Kokot и др. [8] также считают, что WFI более подходит, чем страхование отдельных культур, и может быть применено в Сербии.
Комплексное страхование фермы также увеличивает благосостояние производителя больше, чем страхование отдельных культур, потому что оно концентрирует вероятности более тесно вокруг среднего значения. WFI является более эффективной политикой, если фермеры имеют схожий уровень неприятия риска. Затраты на администрирование этого страхования ниже, чем у других полисов. Действительно, комплексное страхование фермы позволяет фермерам, понесшим убытки, получить компенсацию за счет других продуктов. Структурно комплексное страхование фермы аналогично портфельному страхованию, но взаимосвязи и корреляции между продуктами могут не учитываться.
2. Предпосылки и обзор литературы
В последние годы многие аграрные экономисты сосредоточились на новых страховых политиках, включая WFI, и некоторые исследователи оценили благосостояние производителей при таком страховании. Например, Hennessy и др. [7] исследовали финансовые эффекты и эффекты благосостояния этих страховых политик, определив, что комплексное страхование фермы выгодно фермерам с точки зрения расходов и покрытия рисков. Они дополнительно утверждали, что комплексное страхование фермы может предоставлять более высокие уровни покрытия благодаря своему разнообразию, которое смягчает риск и снижает потенциальные проблемы морального риска, связанные со страховыми программами. Meuwissen и др. [9] утверждали, что комплексное страхование фермы более привлекательно, поскольку представляет собой практичный вариант для оптимизации благосостояния фермеров. Berg [10] использовал дисперсию математического ожидания и симуляцию Монте-Карло для оценки влияния на уровне фермы страхования дохода и урожайности, а затем симулировал страховое покрытие. Результаты показали, что у фермеров есть достаточная мотивация для приобретения многорискового страхования, так как оно значительно снижает волатильность дохода и способствует специализации в планировании производства сельскохозяйственных культур. Hart и др. [11] изучали политику комплексного страхования фермы и обнаружили, что для покрытия в 95% или менее справедливые премии для крупного рогатого скота на различных фермах Айовы заметно ниже, чем индивидуальные премии для кукурузы на тех же фермах. Bielza и Garrido [12] оценили потенциал комплексного страхования фермы по сравнению со страхованием отдельных культур для слив, абрикосов и винограда в валенсийском сообществе Испании, заключив, что комплексное страхование фермы было сравнительно более благоприятным. Turvey [5] исследовал влияние страхования дохода всей фермы на выбор портфеля фермы для репрезентативной фермы в Манитобе, Канада, используя модель среднего-дисперсии для минимизации риска и модель среднего-скошенности для максимизации скошенности. Исследование показало, что фермеры значительно изменяют свои сельскохозяйственные стратегии в зависимости от типа предоставляемого страхования. Coble и др. [13] создали практичную программу комплексного страхования фермы, исследуя ее в трех сценариях: отсутствие страхования, комплексное страхование фермы с 90% покрытием и настраиваемая программа комплексного страхования фермы (CAWFI) с ограничениями по охвату и уровню покрытия. Результаты продемонстрировали, что оптимальная программа CAWFI дает сопоставимый эквивалент надежности с альтернативными сценариями. Однако они отметили, что наложение ограничений на охват и уровень покрытия может снизить ее эффективность. Исследователи предложили настраиваемую программу комплексного страхования фермы в качестве альтернативной политики для устранения некоторых известных недостатков существующих конструкций. Chalise и др. [14] разработали модель на основе настраиваемого территориального комплексного страхования фермы (CAWFI) и применили ее к четырем штатам США: Канзас, Северная Дакота, Иллинойс и Миссисипи. Их исследование показало, что ограниченная конструкция CAWFI значительно снижала риск при гораздо более низких затратах по сравнению с FWFI. Marković и Kokot [15] исследовали комплексное страхование дохода фермы, оценивая страхование четырех культур в Сербии: яровой пшеницы, кукурузы, сои и подсолнечника. Программа заявляла о возможности защитить предприятия от природных и климатических рисков и поддержать рыночные риски. Ее премии и административные затраты были низкими, и, в отличие от традиционного сельскохозяйственного страхования, она избегала несостоятельного выбора и моральных рисков. Luckstead и Devadoss [16] использовали кумулятивную теорию перспектив для разработки теоретической модели покрытия ценового риска и культур, сосредоточившись на дополнительных вариантах покрытия для оптимальных решений по покрытию доходов для лиц, не склонных к риску. Они исследовали влияние политик на производителей пшеницы, используя непараметрический подход для оценки двумерных распределений урожайности и цен на пшеницу в округе Митчелл, Канзас. Результаты показали, что фермер был бы готов нести большие убытки из-за более высокого уровня покрытия, но уровень покрытия не может быть увеличен, потому что фермер уже выбрал максимально допустимый уровень покрытия защиты дохода. Следовательно, фермер готов взять на себя больший базисный риск, полагаясь больше на вариант дополнительного покрытия на уровне округа, снижая уровень покрытия для уменьшения средних затрат. Kokot и др. [8] исследовали возможность внедрения комплексного страхования дохода фермы в Сербии. Они отметили, что из-за засухи в исследуемом районе урожайность и ожидаемые доходы снизились, что давало фермерам право на компенсацию в размере 5697 долларов США. Однако фермеры должны были заплатить комиссию за передачу риска в размере 373 долларов США страховой компании. Исследование продемонстрировало, что комплексное страхование дохода фермы может быть применено в таких странах, как Сербия. Biram и др. [17] исследовали роль страхования дохода в смягчении рисков урожайности и цен для кукурузы и сои в четырех регионах Канзаса, США. Они использовали бета-распределение для симуляции урожайности и логнормальное распределение для симуляции цены. Результаты выявили, что для оптимального управления рисками производители должны выбирать свой уровень страхового покрытия, причем идеальное покрытие дохода должно находиться в диапазоне 76–86 процентов покрытия сельскохозяйственного риска. Falsafian и др. [18] определили, что территориальное страхование урожайности культур предоставляет положительные выгоды для благосостояния и может служить практичной альтернативой или дополнением к существующим программам страхования урожая в Иране. Более того, его успех в других странах предполагает, что это может быть подходящей программой управления рисками для развивающихся стран, таких как Иран.
Согласно контексту, комплексное страхование фермы — это новая модель, которая разработана для удовлетворения потребностей диверсифицированных ферм, выращивающих разнообразные продукты и продающих на местные, региональные или специализированные рынки или напрямую. Современное управление рисками в сельском хозяйстве все больше фокусируется на страховании доходов фермы. Цель этой политики — объединить все риски фермы в единый контракт, предлагая множество преимуществ по сравнению с традиционным страхованием. В отличие от традиционного страхования, комплексное страхование фермы не подвержено проблемам морального риска и неблагоприятного отбора. Комплексное страхование фермы предоставляет более эффективное покрытие, чем страхование отдельных продуктов, по единому контракту. Дополнительно, комплексное страхование фермы приносит пользу производителям и улучшает эффективность государственных страховых субсидий. Учитывая недостаток исследований по комплексному страхованию фермы и его эффектам на благосостояние в Иране, существует насущная потребность в современных страховых программах, таких как WFI, в стране. Следовательно, это исследование может предоставить соответствующее руководство по расчету тарифов премий для политиков, одновременно подчеркивая его влияние на благосостояние для стимулирования участия фермеров.
3. Материалы и методы
Модельная структура включает оценку страховых премий для страхования отдельных культур (CSI) и комплексного страхования фермы в зависимости от количества приобретенных страховых полисов и количества застрахованных культур. Если коэффициенты убыточности часто страхуемых фермеров ниже при различных страховых стратегиях в группах и по культурам, то политика комплексного страхования фермы, которая интегрирует все полисы в одну программу, должна быть разумной.
Предположим, что фермер выращивает N культур, и каждая культура i имеет функцию распределения вероятностей урожайности 𝑓𝑖(𝑥𝑖). Bielza и Garrido [12] показали, что актуарно справедливая премия для многорискового страхования отдельных культур для каждой культуры (Pri) будет оценена по уравнению (1).
где 𝐼˜𝑖 — страховая выплата по культуре i; E[.] — оператор математического ожидания; 𝑋¯𝑖 — гарантированная урожайность для культуры i; 𝑥˜𝑖 — стохастическая урожайность; pi — цена культуры, по которой выплачиваются потери урожая, предполагаемая неслучайной; 𝑙˜𝑖 — случайная потеря, имеющая право на компенсацию (которая не всегда соответствует потере фермера); и 𝜆˜𝑖 указывает на вероятность получения компенсации, когда урожайность ниже застрахованного уровня. По сути, функция этой переменной — отразить случай, когда низкая урожайность возникает по причине, которая либо ведет (𝜆˜𝑖 = 1), либо не ведет (𝜆˜𝑖 = 0) к компенсации, как определено страховой политикой. Для полиса WFI справедливая премия будет результатом следующего:
где R — застрахованный доход, специфичный для фермы. Он равен ожидаемому доходу (при разработке сельскохозяйственного страхования доход фермеров приоритетнее прибыли для упрощения расчетов премий и минимизации административных затрат, также повышая практичность страховой программы), который ферма получила бы, если бы все культуры были охвачены полисами страхования отдельных культур, как показано в следующем уравнении:
где Pr специфичен для фермера, потому что для его расчета необходимы структуры посевных площадей, Si. Более того, поскольку функции урожайности культур, как правило, не независимы, численный расчет Pr и Pri также требует корреляций между случайными переменными 𝑙˜𝑖 и 𝑥˜𝑖.
Экономию с точки зрения страховых затрат при том же ожидаемом доходе можно измерить с помощью уравнения (4):
Дополнительно, выигрыши в полезности можно оценить с помощью уравнения (5):
где 𝜋˜ — прибыль фермы при различных страховых полисах; U(π) — функция полезности DARA или CRRA, такая как 𝑈(𝜋)=𝜋1−𝑟1−𝑟; и r — коэффициент относительного неприятия риска. Соответственно, разница эквивалентов определенности также была рассчитана следующим образом:
Отметим, что, согласно всем определениям WFI, разница в ожидаемой прибыли такова:
Поскольку
где Ci — затраты на культуру i. Оба результата равны подразумеваемому застрахованному доходу (R) минус производственные затраты на культуры, потому что премия считалась актуарно справедливой.
Обратим внимание на следующее в уравнении (2): (i) когда потерь нет, конечная урожайность равна 𝑥˜𝑖; (ii) когда есть имеющая право на возмещение потеря (𝜆˜𝑖 = 1), конечная урожайность равна гарантированной урожайности 𝑋¯𝑖; и (iii) когда потеря не имеет права на страховую выплату (𝜆˜𝑖 = 0), урожайность равна 𝑥˜𝑖 (при 𝑥˜𝑖 < 𝑋¯𝑖). Также отметим, что в уравнении (2) переменная 𝜆˜𝑖 применяется только когда 𝑥˜𝑖 < 𝑋¯𝑖.
Как упоминалось ранее, в страховании сельскохозяйственного дохода есть особенно важные факторы: во-первых, страховая сумма, которая отражает ожидаемый доход и определяет условия компенсации, и, во-вторых, страховые премии, которые отражают сумму ожидаемой компенсации и выплачиваются на основе уровня покрытия. Оба этих фактора зависят от распределения урожайностей, и, следовательно, точность их определения зависит от правильного определения распределения урожайности и цены для продукта, а также степени корреляции. Goodwin и Mahul [19] предложили, что для прогнозирования распределения вероятностей дохода фермеров должны быть установлены функции плотности вероятностей для урожайностей и цен продуктов. Поэтому любая процедура расчета тарифов премий связана с измерением риска дохода. В исследовании использовалось совместное распределение вероятностей цен и урожайностей.
3.1. Моделирование распределения урожайности и подходы к прогнозированию
Поскольку WFI предназначено для стабилизации дохода фермеров, необходимо прогнозировать будущие значения урожайностей и цен. Урожайность культур имеет тенденцию увеличиваться со временем из-за технологических достижений, что подразумевает, что процесс генерации данных нестабилен. Следовательно, некорректно сравнивать наблюдаемые урожайности за различные периоды времени. Чтобы решить эту проблему, было предложено много методов для устранения тренда или нормализации данных об урожайности. Согласно Zhu и др. [20], обычно используемым методом является двухэтапный процесс оценки. В этом процессе на первом этапе урожайности прогнозируются с использованием параметрических или непараметрических моделей. На втором этапе урожайности культур детрендируются. В литературе использовались различные регрессионные модели, включая линейные [19,21,22], квадратичные [22,23] и полиномиальные модели [24]. Дополнительно, Deng и др. [25] и Vedenov и др. [26] применяли лог-линейную модель, в то время как Adhikari и др. [22] и Harri и др. [27] применяли методы билинейных сплайнов и узлов. Также Ker [28], Goodwin и Ker [29] и Ker и Goodwin [30] использовали стохастическую модель, такую как авторегрессионная интегрированная скользящая средняя (ARIMA), для прогнозирования урожайностей. Существует два общих подхода к устранению тренда урожайностей. Эти два подхода основаны на предположениях о постоянных и непостоянных ошибках.
Если исследователь предполагает, что величина ошибки не зависит от уровня урожайности, то он добавляет все остатки к базовому году (последнему году периода наблюдений). Однако если считается, что отклонения от тренда пропорциональны уровню урожайности, то можно рассмотреть построение нормализованной урожайности следующим образом:
где ytdet — детрендированная урожайность в году t; yt и ŷt — наблюдаемые и прогнозируемые значения урожайностей соответственно; и ŷT — прогнозируемое значение урожайности в базовом году, которым в данном исследовании является 2021 год. Таким образом, потенциальная проблема гетероскедастичности также будет исправлена. В контексте методы, используемые в моделях распределения урожайности, делятся на три широкие группы: параметрические, полупараметрические и непараметрические методы [21]. После детрендинга и нормализации урожайностей распределение вероятностей урожайности оценивалось с использованием параметрического или непараметрического подхода. Основное преимущество использования параметрического подхода (бета, нормальное, логнормальное, гамма, логистическое и Вейбулла) — простота оценки параметров распределения, но при расчете тарифов для продуктов страхования урожая эти распространенные параметрические распределения часто представляют проблемы, такие как неспособность моделировать бимодальность или многомодальность; поэтому некоторые исследователи предпочитают использование непараметрических методов, которые определяют форму распределения без заданной априорной спецификации. Оценка ядра используется как непараметрический метод для оценки формы условной плотности цен и урожайности и расчета стоимости контракта страхования урожая, который также использовался в этом исследовании [18]. В этом исследовании, в зависимости от природы данных и на основе литературы, использовался второй подход. В этом методе временные ряды урожайностей продукта сопоставляются с переменной тренда (в линейной или логарифмической, или квадратичной форме). Затем среди этих линейных, логарифмических и линейно-логарифмических моделей выбирается подходящая модель на основе критериев соответствия, включая преобразование [31].
3.2. Моделирование распределения цен
В страховании дохода страховая компания защищает держателя полиса от снижения урожайности культур и цен. Таким образом, страхование дохода включает прогнозирование урожайностей и цен на время сбора урожая для построения тарифов премий. Цены на культуры растут со временем, особенно в развивающихся странах. В таких случаях некорректно сравнивать цены в различные периоды. В экономических терминах, остатки подвержены гетероскедастичности. Таким образом, перед моделированием стохастические компоненты ценовых рядов должны быть разделены. В этом исследовании номинальные цены на культуры, полученные фермерами в период 1983–2018 гг., были получены с веб-сайта Министерства сельского хозяйства. Затем ценовые ряды были преобразованы в реальные данные с использованием дефлятора индекса цен производителей (PPI), опубликованного Центральным банком Ирана. Поскольку дефлированные номинальные данные не могут учесть прямое влияние изменений в технологии и структуре рынка, необходимо устранить тренд в данных, чтобы отделить стохастический компонент от ценовых рядов. В этом исследовании ценовые ряды были детрендированы с помощью линейных, квадратичных, полиномиальных и лог-линейных регрессионных моделей, а также моделей авторегрессионной интегрированной скользящей средней (ARIMA). Затем остатки проверялись на нормальность и свойства белого шума. Наконец, было определено наилучшее распределение для каждого ценового ряда.
3.3. Измерение риска дохода
Как упоминалось ранее, риск дохода — это комбинация неопределенностей цены и урожайности. В целом, полисы страхования дохода защищают производителей от низких цен и низкой урожайности культур. Если доход падает ниже гарантированного уровня из-за сочетания низкой урожайности и/или низких цен, застрахованный фермер получает компенсацию, равную разнице между фактическим и гарантированным доходом. Для измерения риска дохода требуется определить вероятность возникновения цены и прибыли. Для достижения этого, на первом этапе, необходимо точно оценить риски цены и урожайности. Однако плотности цен и выпуска часто не независимы [11,32].
3.4. Измерение благосостояния фермеров
В этой статье основная идея оценки влияния комплексного страхования фермы (WFI) состоит в сравнении благосостояния фермеров при альтернативных сценариях. В статье выдвигаются две гипотезы сценариев, включая отсутствие страхования урожая и комплексное страхование фермы (WFI). Процесс достижения этого требует оценки благосостояния фермеров. В экономической теории использование модели ожидаемой полезности является наиболее общим подходом к сравнению рискованных вариантов и изучению рискованного поведения в условиях неопределенности. Поэтому в этой статье была разработана симуляционная модель, основанная на функции ожидаемой полезности, для оценки благосостояния фермеров. Аналогично предыдущим исследованиям [33,34,35,36], в этой статье применялась степенная функция полезности (уравнение (11)) для вычисления полезности фермеров [37].
где θ представляет постоянное относительное неприятие риска (CRRA) и установлено равным 2 для проверки устойчивости анализа. Более того, W0 представляет начальное богатство фермера, а W — чистый доход фермера.
Предполагается, что фермеры стремятся максимизировать ожидаемую полезность своего конечного богатства в условиях неопределенности. Оценка ожидаемой полезности от выбора страхования как инструмента управления рисками зависит от предпочтений риска фермеров и их субъективной оценки рисков, с которыми они сталкиваются. В этом анализе предполагается, что фермеры не склонны к риску и имеют предпочтения риска, соответствующие функции CRRA. Функция CRRA подразумевает, что решение индивида не меняется с точки зрения доли бюджета, или эластичности дохода равны 1. Математически функция полезности, предполагающая CRRA, выглядит следующим образом:
В уравнении (12) W — чистое стохастическое конечное богатство для выбора конкретного страхования, а r — коэффициент относительного неприятия риска (коэффициент Эрроу–Пратта). Конечное богатство (уравнение (13)) включает начальное богатство фермера, страховые премии (за вычетом субсидии), фактический доход и страховые выплаты.
где πi (α) — конечное богатство, BW — начальное богатство, p — цена продукта, y — урожайность продукта, I(α) — полученные страховые выплаты, 𝛾 — страховая премия, а C — производственные затраты.
Начальное богатство и производственные затраты предполагаются постоянными для всех страховых полисов. Чистая страховая премия выплачивается фермером после субсидии, которая различается для каждого страхового полиса и уровня покрытия. Фактический доход является произведением n симуляций цен и урожайностей на момент сбора урожая. Различные варианты управления рисками были исследованы с помощью эквивалента определенности (CE) чистого стохастического конечного богатства (W). Этот анализ использовал модель, согласующуюся с [38,39,40,41,42], используя функцию полезности CRRA. Ожидаемая полезность выглядит следующим образом:
Здесь E представляет оператор математического ожидания, а ω — вероятность соответствующего конечного богатства. r было установлено равным 2 для представления умеренного неприятия риска, что использовалось в нескольких предыдущих исследованиях, таких как [38,39,41,42]. Гарантированный уровень страхования был получен как произведение ожидаемой урожайности, уровня страхового покрытия и ожидаемой полезности для различных уровней покрытия с помощью симуляции Монте-Карло.
В этом исследовании CE рассчитывался из функции ожидаемой полезности, как показано в уравнении (4). CE — это мера ожидаемых выгод, которая рассчитывается с учетом всех затрат и субсидий, связанных с сельскохозяйственным производством, страховыми затратами и начальным богатством фермера. Выгоды будут выше, если фермер выберет страхование с более высоким CE. Результаты выражены как чистая выгода на гектар для более простой интерпретации. Это рассчитывается как разница двух CE, представленных в уравнении (5): CE для страхования с определенным уровнем покрытия и CE0 для отсутствия страхования [43]. Эта разница делится на чистые гектары, чтобы представить результаты в риалах на гектар, как показано в уравнении (15).
Следовательно, ожидаемую компенсацию можно рассчитать с помощью уравнения (16).
где EI — ожидаемая компенсация; LT — гарантированная сумма; а IS — смоделированный доход. Смоделированный доход определяется на основе соответствующих распределений, таких как параметрическое распределение для урожайностей и цен. Другими словами, доход отдельного фермера моделируется в соответствии с распределением вероятностей. Для этого смоделированная индивидуальная урожайность умножается на смоделированные цены. Следовательно, чистый доход можно рассчитать согласно уравнению (17).
где R больше 1 и является коэффициентом относительного неприятия риска, а πi — гарантированный доход на гектар. Гарантированный уровень страхования — это произведение ожидаемой урожайности и уровня покрытия. Предполагая, что фермер выбирает уровень страхового покрытия для максимизации своей ожидаемой полезности, проблема принятия решения фермером задается следующим образом:
Максимизированные ожидаемые полезности в уравнении (18) преобразуются в связанные эквиваленты определенности для каждого случая с использованием уравнения (19):
В этом исследовании эквивалент определенности оценивался для диапазона уровней покрытия при различных сценариях. Затем благосостояние фермера рассчитывалось на основе разницы между эквивалентом определенности на гектар для каждого случая и случаями без страхования [22].
3.5. Место исследования и данные
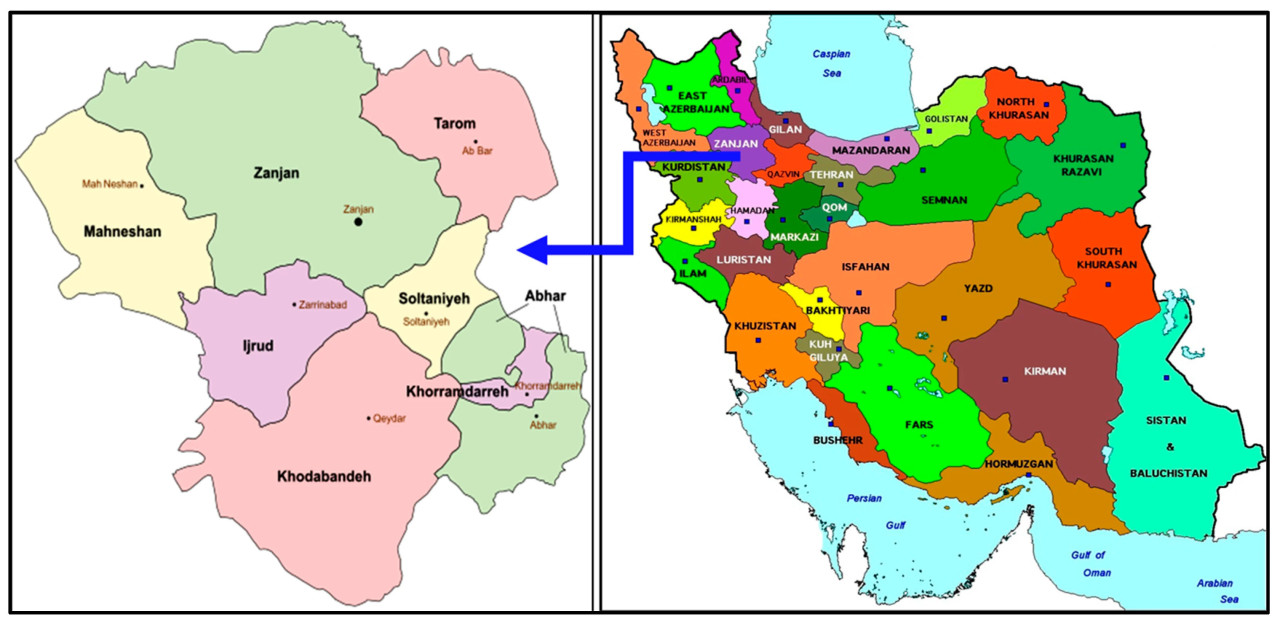
Иран расположен в Северо-Западной Азии, с площадью 1 648 195 км² и населением около 85 миллионов человек. Столица этой страны — Тегеран. Провинция Зенджан находится на северо-западе Ирана, с площадью 22 164 км² и населением 1,1 млн человек. Географическое расположение провинции Зенджан в Иране показано на рисунке 1 [44].
Рисунок 1. Расположение провинции Зенджан в Иране. Источник: [44].
В провинции Зенджан сельскохозяйственный сектор играет ключевую роль в экономике. Пшеница, ячмень и люцерна являются основными культурами провинции, занимая примерно 65% от общей посевной площади [45]. В этом исследовании используются исторические данные об урожайности как на уровне ферм, так и на уровне округов, вместе с ценами на ферме, полученными из провинциальной сельскохозяйственной организации, для оценки ожидаемых урожайностей и цен. Данные об урожайности на уровне ферм в провинции Зенджан охватывают 7-летний период с 2015 по 2021 год, в то время как исторические урожайности на уровне округов доступны с 1981 по 2018 год. Цены выражены в иранской валюте (IRR) за килограмм продукции [45]. В сельскохозяйственном году 2020–2021 фермеры провинции Зенджан выделили около 445 000 гектаров под сельскохозяйственное производство, получив более 2,09 млн тонн культур [46]. Одновременно было выдано около 14 500 полисов сельскохозяйственного страхования, из которых 2 203 специально для полевых культур, охватывающих 42 734 гектара пахотных земель в регионе. В сельскохозяйственном году 2020–2021 Провинциальный Фонд сельскохозяйственного страхования собрал общую премию в размере 253 011 млн иранских риалов, включая 30 052 млн иранских риалов от полевых культур и 10 897 млн иранских риалов от фермеров. Однако в течение сельскохозяйственного года 2018-19 общая компенсация, выплаченная сельскохозяйственным подсекторам провинции Зенджан, составила 100 414 млн иранских риалов, из которых 12 000 млн иранских риалов было выделено на полевые культуры. Это указывает на коэффициенты убыточности 0,40 и 1,1 для сельскохозяйственного сектора и полевых культур соответственно, что предполагает дефицит для фонда сельскохозяйственного страхования. Более того, существующая система сельскохозяйственного страхования не отвечает своим дополнительным целям, таким как гарантирование экономической безопасности фермеров, стимулирование инвестиций в сектор и обеспечение соответствующего роста отрасли. Следовательно, становится очевидной необходимость исследования практичности новых страховых политик.
Это исследование включало сбор данных временных рядов по посевной площади, урожайности и ценам на культуры пшеницы, ячменя и люцерны с сельскохозяйственных годов 1982–83 по 2020–21. Дополнительно, данные об урожайности отдельных фермеров в течение сельскохозяйственных годов 2008–2009 и 2020–2021 были получены из провинциальной Организации сельскохозяйственного джихада. Средняя урожайность за 10-летний период была определена для 30 выбранных фермеров. Впоследствии были разработаны три сценария для политики комплексного страхования дохода фермы.
1. Страхование дохода одной культуры отдельно для пшеницы, ячменя и люцерны.
2. Комплексное страхование дохода фермы для двух культур: пшеница–ячмень, пшеница–люцерна и ячмень–люцерна.
3. Комплексное страхование дохода фермы в случае трех культур одновременно (пшеница, ячмень и люцерна).
Пакеты Simetar 5.0 и Stata 15.1 MP использовались для оценки эконометрических моделей путем оценки функций плотности вероятности и кумулятивной функции распределения и симуляции урожайностей и цен.
4. Результаты
4.1. Проверка на стационарность
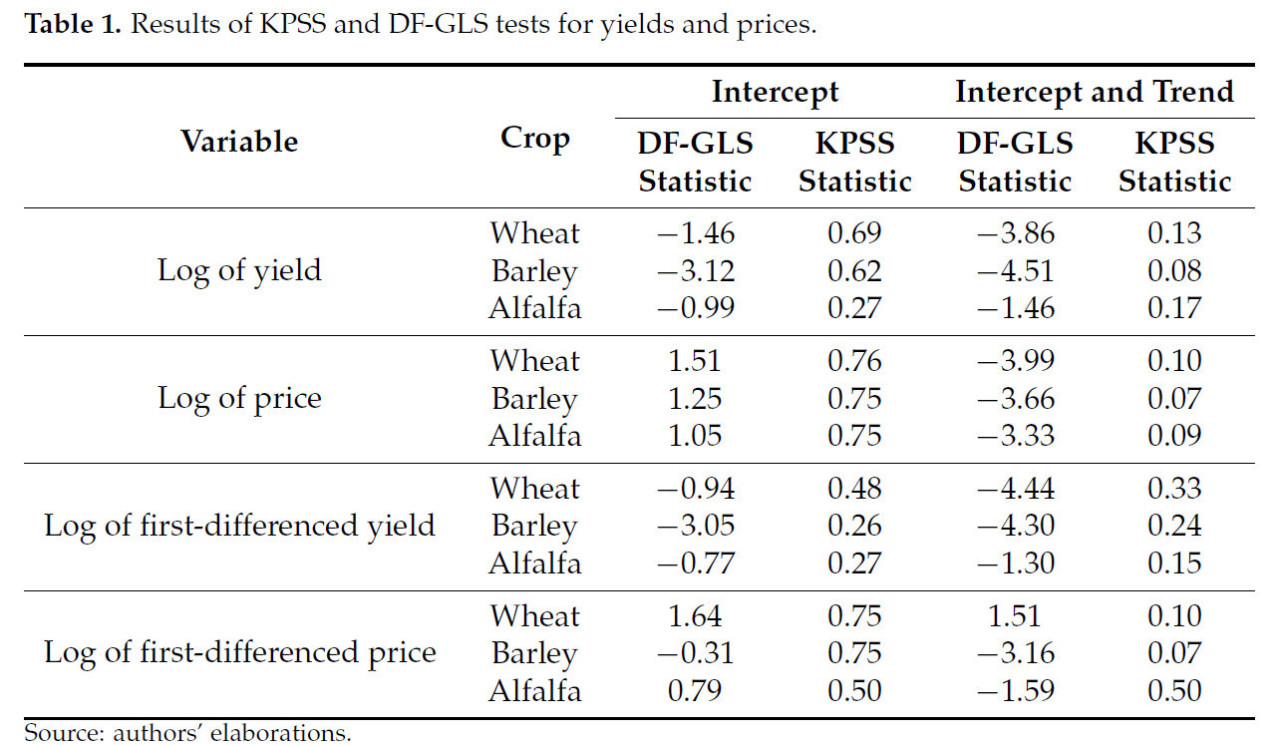
В этом исследовании тесты DF-GLS на единичный корень и KPSS использовались для проверки стационарности урожайностей и цен культур, и результаты представлены в таблице 1. Учитывая, что критические значения теста DF-GLS в модели, включающей константы, на 1% и 5% составляют −2,64 и −1,95 соответственно, а для моделей, включающих константу и тренд, они составляют −3,77 и −3,19 соответственно, мы понимаем, что логарифмы урожайности пшеницы и ячменя не имеют единичного корня и стационарны на уровне данных. В то же время урожайность люцерны была нестационарной. Дополнительно, критические значения для теста KPSS в модели, включающей константы, на 1% и 5% составляют 0,74 и 0,46 соответственно, а для моделей, включающих константу и тренд, они составляют 0,22 и 0,15 соответственно. Результаты теста KPSS также подтверждают стационарность урожайностей и цен и приводят нас к использованию модели регрессии с трендом для детрендинга урожайностей и модели ARIMA для детрендинга цен. Для определения типа распределения переменных использовались детрендированные значения. Линейные и квадратичные регрессионные модели использовались для детрендинга урожайностей, а модели ARIMA применялись для детрендинга цен. Тест преобразования Бокса–Кокса [31] был применен для выбора подходящей модели среди линейных, квадратичных и логарифмических моделей. В таблице 2 представлены описательные статистики исторических цен и урожайностей для пшеницы, ячменя и люцерны после детрендинга данных.
Таблица 1. Результаты тестов KPSS и DF-GLS для урожайностей и цен.
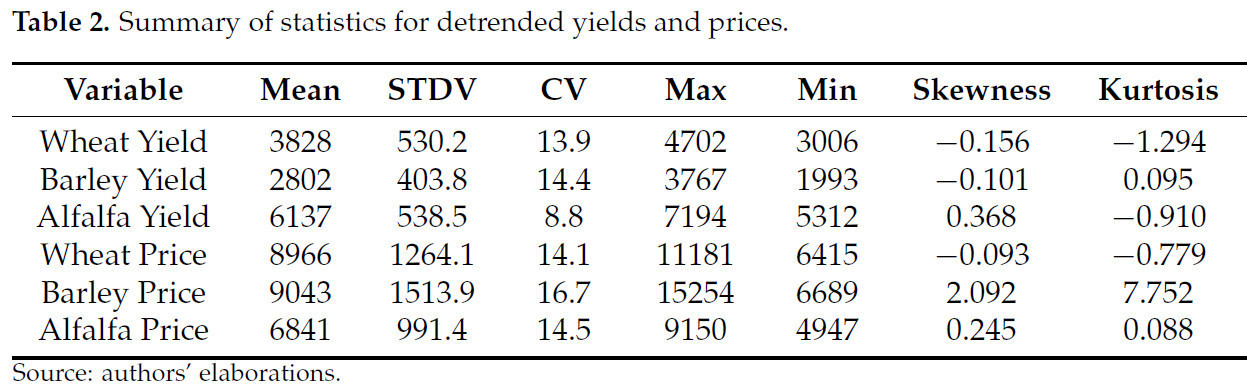
Таблица 2. Сводная статистика для детрендированных урожайностей и цен.
Исследование коэффициента вариации (CV) в таблице 2 показывает, что урожайность люцерны менее изменчива, чем у пшеницы и ячменя. Движения цен на пшеницу менее рассеяны, чем у ячменя и люцерны, что ожидаемо и разумно, учитывая гарантированную цену продукта. Урожайности пшеницы и ячменя и цены на пшеницу имеют левостороннюю асимметрию. Левостороннее асимметричное распределение имеет длинный хвост на левой стороне и подразумевает, что хвосты толще справа, с урожайностями и ценами, близкими к максимальному наблюдаемому значению, встречающимися чаще, чем низкие урожайности и цены. В то же время урожайность и цены люцерны, а также цены на ячмень имеют тенденцию к правосторонней асимметрии. Правостороннее асимметричное распределение длиннее на правой стороне своего пика, чем на левой. Дополнительно, коэффициенты эксцесса для урожайности пшеницы, урожайности люцерны и цены на пшеницу отрицательны, в то время как они положительны для урожайности ячменя, цены на ячмень и цены на люцерну.
4.2. Прогнозирование будущих цен и урожайностей
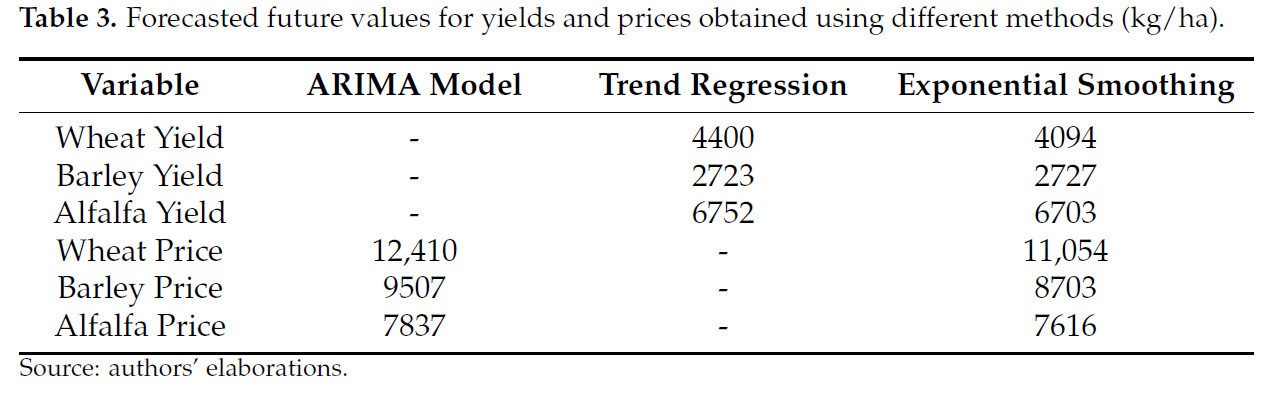
Оценка будущих урожайностей и цен для каждого продукта необходима для расчета гарантированного дохода. Для этой цели использовались различные методы, включая параметрические подходы, такие как регрессия тренда и моделирование ARIMA, а также непараметрическая техника экспоненциального сглаживания. Прогнозируемые значения урожайностей и цен, полученные каждым методом, представлены в таблице 3.
Таблица 3. Прогнозируемые будущие значения урожайностей и цен, полученные с использованием различных методов (кг/га).
Как показано в таблице 3, различные методы предоставляют различные прогнозы урожайностей и цен. Тесты Бройша–Годфри и Q-статистики использовались для проверки характеристик белого шума у члена возмущения модели как индикатора адекватности моделей ARIMA. Q-статистика для первой разности членов остатков незначима, и остатки находятся в пределах диапазона. Более того, статистика LM теста Бройша–Годфри незначима при проверке последовательной автокорреляции членов возмущения, что подтверждает адекватность выбранной модели.
4.3. Расчет совокупного лимита выплат и тарифов премий
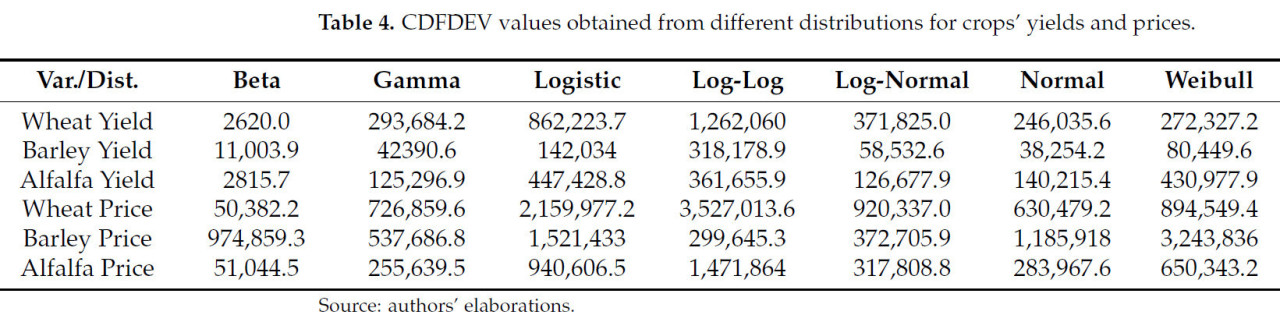
Для определения наилучшего параметрического распределения для урожайностей и цен использовались Отклонения Кумулятивной Функции Распределения (CDFDEVs). CDFDEVs указывают на отклонение распределения от эмпирического распределения. Поэтому, чем ниже CDFDEV, тем более подходящей является CDF для описания распределения плотности. Результаты различных распределений для детрендированных урожайностей и цен пшеницы, ячменя и люцерны представлены в таблице 4. Как показывают данные в таблице 4, бета-функция распределения является наилучшим выбором для описания урожайностей пшеницы, ячменя и люцерны, в дополнение к ценам на пшеницу и люцерну, в то время как лог-логистическое распределение является наилучшим вариантом для описания цены на ячмень.
Таблица 4. Значения CDFDEV, полученные из различных распределений для урожайностей и цен культур.
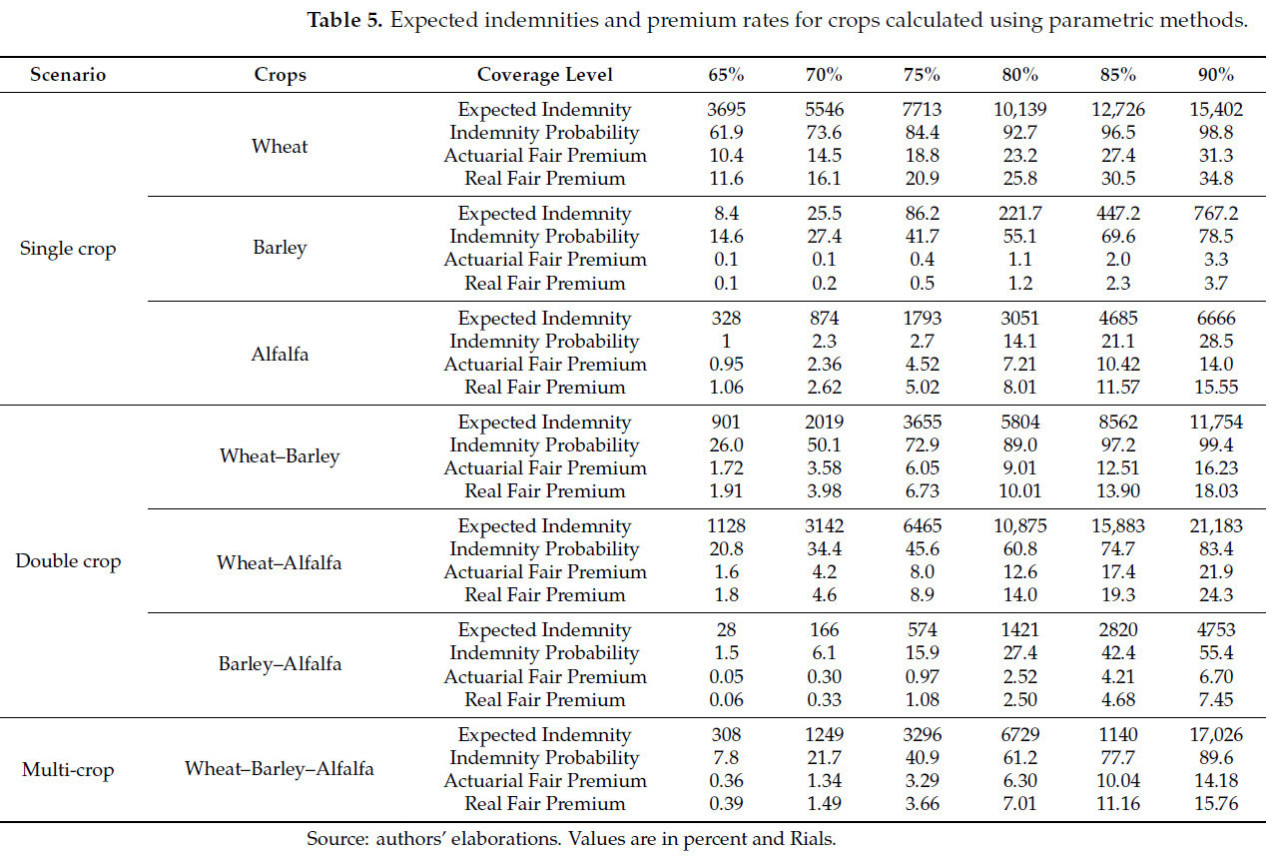
После выбора наиболее подходящей функции плотности вероятности, гарантированные доходы от культур были оценены с использованием совместного распределения урожайностей и цен на различных уровнях покрытия. На следующем этапе ожидаемая компенсация от страховой компании была рассчитана на основе смоделированного и гарантированного дохода. Наконец, тарифы премий были рассчитаны для сценариев с одной, двумя и тремя культурами согласно трем уровням покрытия от 65 до 90%, как представлено в таблице 5. Цифры в таблице 5 показывают, что в случае выращивания только одной культуры ожидаемая компенсация для пшеницы является наивысшей, а для ячменя — наинизшей. В случае двух культур, наивысшая ожидаемая компенсация была для пшеницы–люцерны, а наинизшая — для ячменя–люцерны. Ожидаемая страховая выплата для трех культур ниже, чем для двух культур пшеница–ячмень и пшеница–люцерна, и выше, чем для комбинированного страхования ячменя и люцерны. Таблица 5 также показывает, что риск дохода пшеницы выше, чем у других продуктов. Люцерна имела самый низкий риск дохода по сравнению с пшеницей и ячменем. Дополнительно, вероятность компенсации по программе одной культуры была наивысшей для пшеницы по сравнению с другими культурами и наинизшей для люцерны. Для двух культур вероятность компенсации была наинизшей в случае ячмень–люцерна и наивысшей в случае пшеница–ячмень.
Таблица 5. Ожидаемые страховые выплаты и тарифы премий для культур, рассчитанные с использованием параметрических методов.
Как показано в таблице 5, вероятности компенсации для трех культур ниже, чем для пшеницы и ячменя и для двух культур пшеница–ячмень и пшеница–люцерна, что подразумевает, что WFI, страхуя урожайности и цены, снижает риск ущербов и компенсаций. Основываясь на таблице 5, наивысший реальный тариф премии в программе одной культуры — для пшеницы, а наинизший — для ячменя. В случае двух культур, наивысшая реальная премия — для программы пшеница–люцерна, а наинизшая — для программы ячмень–люцерна. Дополнительно, реальные тарифы премий для трех культур ниже, чем отдельные реальные тарифы премий для пшеницы и люцерны, и выше, чем реальные тарифы премий для ячменя. Более того, реальные тарифы премий этих трех культур ниже, чем реальные тарифы премий пшеница–ячмень и пшеница–люцерна, и выше, чем комбинированные тарифы премий ячменя и люцерны. Следовательно, можно заключить, что с увеличением количества застрахованных культур реальные и актуарные тарифы премий снижаются, что показывает превосходство и высокую эффективность политики WFI по сравнению со страхованием культур по отдельности.
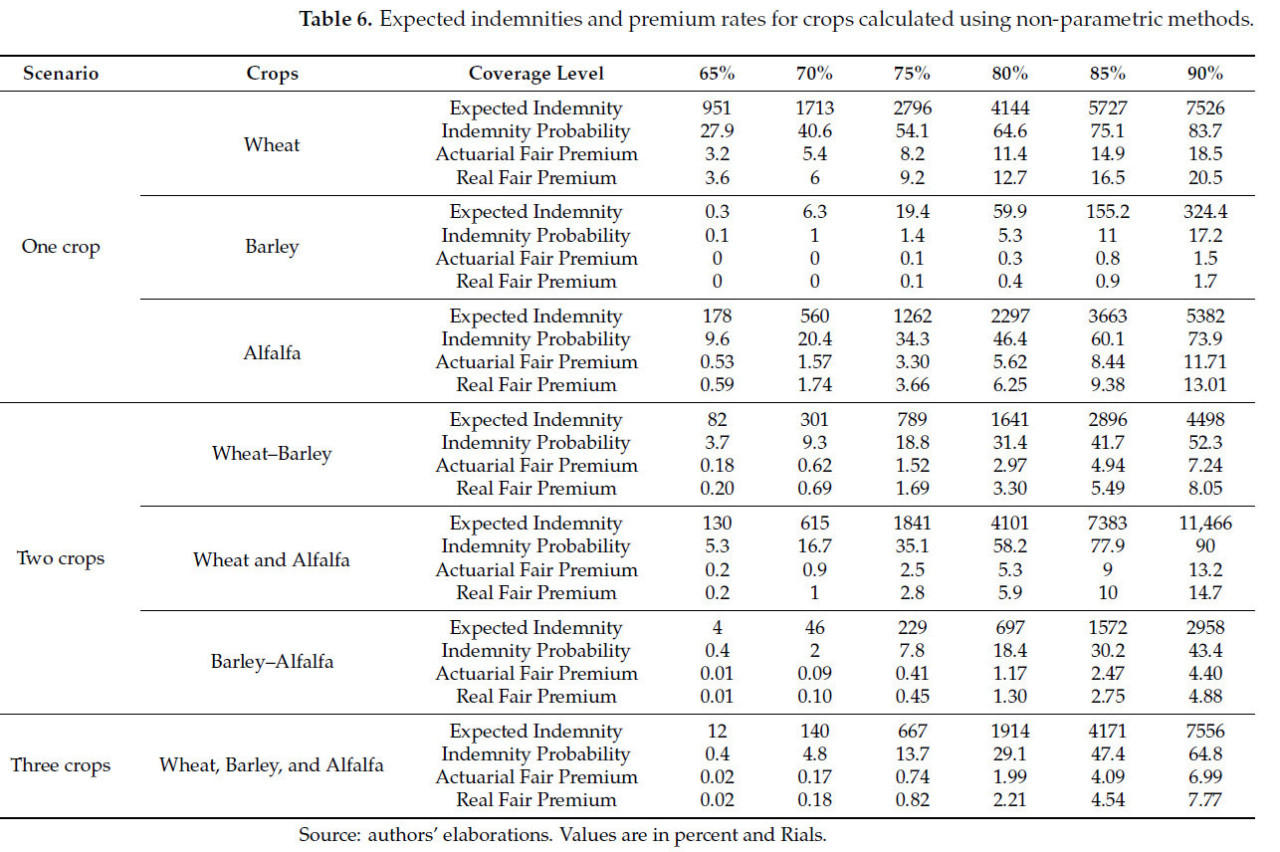
Чтобы выбрать наилучший метод для оценки ожидаемой компенсации, вероятности выплаты, актуарных и реальных тарифов премий в программе комплексного страхования дохода фермы, также использовался непараметрический подход, и результаты представлены в таблице 6. Результаты в таблице 6 показывают, что в случае одной культуры ожидаемая компенсация пшеницы является наивысшей, а ячменя — наинизшей, что согласуется с результатами параметрических методов. В случае двух культур, наивысшая ожидаемая компенсация принадлежит страхованию пшеница–люцерна, а наинизшая — страхованию ячмень–люцерна, что согласуется с результатами параметрических методов. Более того, таблица показывает, что ожидаемая компенсация в случае трех культур выше, чем для двух культур ячмень–люцерна, но ниже, чем для пшеница–ячмень и пшеница–люцерна. Дополнительно, ожидаемая компенсация для страхования трех культур выше, чем для индивидуального страхования ячменя, но ниже, чем для индивидуального страхования пшеницы и люцерны, что подтверждает результаты параметрических подходов. В общем, сравнение оценок функций вероятности и кумулятивной плотности урожайностей и цен с гистограммами и эмпирическими значениями показывает, что непараметрические оценки более эффективны, чем параметрические оценки. Следовательно, этот метод будет использован на следующих этапах.
Таблица 6. Ожидаемые страховые выплаты и тарифы премий для культур, рассчитанные с использованием непараметрических методов.
4.4. Расчет изменений в благосостоянии фермеров
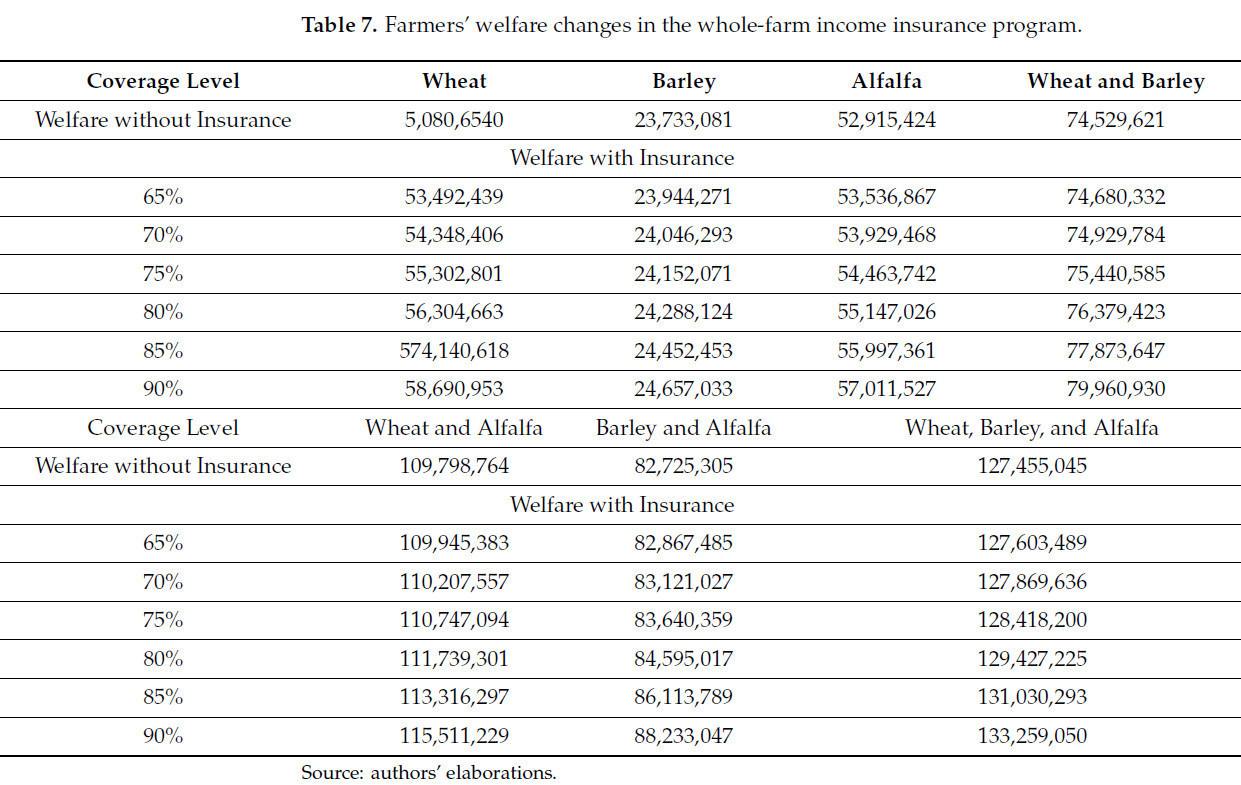
Влияние страхования на благосостояние производителей можно оценить, сравнив разницы эквивалентов определенности со страховым покрытием и без него. Чтобы оценить эффекты участия в программе комплексного страхования фермы на благосостояние фермеров, их благосостояние было вычислено и сравнено со сценарием без страхования. В Иране государство покрывает большую часть страховых премий, поэтому чистый доход фермеров должен быть рассчитан путем определения их доли уплаченной премии. Фонд сельскохозяйственного страхования провинции Зенджан сообщил, что ставки страховой премии фермеров для пшеницы, ячменя и люцерны составляли 22%, 21% и 25% соответственно. Тарифы страховых премий, полученные из двумерной ядерной функции, использовались для симуляции урожайностей и цен культур для расчета дохода фермеров. В таблице 7 обобщены результаты сравнения изменений благосостояния в рамках программы комплексного страхования фермы. Она демонстрирует, что благосостояние производителей увеличилось при участии в программе по сравнению с отсутствием страхования. Например, при покрытии 75%, фермер, страхующий только пшеницу, получает выигрыш в размере 4 496 261 иранских риалов, только ячмень — 418 990 иранских риалов, только люцерна — 1 548 318 иранских риалов, пшеница и ячмень — 900 964 иранских риалов, и пшеница и люцерна — 948 330 иранских риалов. Страхование двух культур (ячмень и люцерна) увеличило бы благосостояние на 915 054 иранских риалов на гектар, в то время как страхование всех трех культур одновременно привело бы к увеличению на 963 155 иранских риалов на гектар.
Таблица 7. Изменения благосостояния фермеров в программе комплексного страхования дохода фермы.
5. Обсуждение
Результаты теста DF-GLS на единичный корень и теста KPSS ожидаемы и согласуются с литературой, в которой утверждается, что ряд урожайности следует процессу стационарности тренда (TSP), а ряд цен следует процессу стационарности разностей (DSP). Поэтому линейные и квадратичные регрессионные модели использовались для детрендинга рядов урожайности, а модели ARIMA применялись для детрендинга рядов цен. Falsafian и др. [18] также обнаружили, что урожайность пшеницы и ячменя в Иране следует TSP. Форма функций распределения указывает, что урожайность пшеницы и люцерны в основном рассеяна слева от среднего по округу, в то время как урожайность ячменя в основном рассеяна справа от среднего по округу. В результате урожайность пшеницы и ячменя в основном ниже, а урожайность люцерны выше, чем региональное среднее. Дополнительно, коэффициенты эксцесса подразумевают, что урожайность пшеницы и люцерны и цены на пшеницу имеют плоское распределение, в то время как урожайность ячменя и цены на ячмень и люцерну показывают островершинное распределение. Аналогично выводам Goodwin и Ker [29] в США, Yonar и др. [47] в Китае и Бангладеш, и Kumar и др. [48] в Индии, урожайности показали отрицательную асимметрию в большинстве случаев, хотя положительная асимметрия была отмечена Chen и Miranda [49].
Наши результаты показывают, что бета-функция распределения подходит для описания урожайностей пшеницы, ячменя и люцерны, а также цен на пшеницу и люцерну, тогда как лог-логистическое распределение лучше всего описывает цены на ячмень. Эти результаты согласуются с результатами Hennessy и др. [7] и Zhu и др. [20]. На следующем этапе были исследованы формы функции плотности вероятности и кумулятивной функции вероятности данных, чтобы убедиться в правильном выборе PDF для описания урожайностей и цен. Согласно [46], графики функций сравнивались с эмпирическими PDF, чтобы проверить их согласованность с фактическими урожайностями и ценами. Из сравнения видно, что гистограмма PDF бета-распределения лучше соответствует эмпирическим PDF, чем другие функции, и, таким образом, бета-распределение лучше всего подходит для описания урожайности пшеницы. В этом исследовании функции вероятности и кумулятивной плотности урожайностей и цен сравнивались с гистограммами и эмпирическими значениями, и мы обнаружили, что непараметрические оценки более эффективны, чем параметрические. Следовательно, этот метод был использован для расчета благосостояния производителя. Эти результаты согласуются с результатами Ozaki и др. [21] для расчета тарифов премий для кукурузы, сои и пшеницы в Бразилии и Falsafian и др. [18] для пшеницы и ячменя в округах Восточного Азербайджана в Иране. Результаты параметрического метода показали, что наивысший реальный тариф премии в программе одной культуры был для пшеницы, а наинизший для ячменя. Для двух культур наивысшая реальная премия была для страхования пшеница–люцерна, а наинизшая для страхования ячмень–люцерна. Дополнительно, реальные тарифы премий для трех культур отличались от реальных тарифов премий для пшеницы, люцерны и ячменя. Фактические тарифы страховых премий для трех культур были ниже, чем фактические тарифы страховых премий для пшеница–ячмень и пшеница–люцерна, и выше, чем комбинированные тарифы премий для ячменя и люцерны. В непараметрическом подходе функции плотности вероятности и кумулятивной плотности переменных были построены с использованием ядерной функции и сравнены с эмпирической кумулятивной функцией плотности. Результаты показали, что наивысшие реальные тарифы премий были для страхования одной культуры (пшеница) и двух культур (пшеница–люцерна). Более того, по мере увеличения количества застрахованных культур тариф премии снижается, что указывает на высокую эффективность комплексного страхования фермы по сравнению со страхованием отдельных культур. Другими словами, контракты комплексного страхования фермы имеют более низкие премии, чем контракты страхования отдельных культур; следовательно, фермеры должны платить меньше.
Оценка изменений в благосостоянии производителя выявляет, что политика WFI превосходит и более эффективна, чем страхование отдельных культур. В частности, одновременное страхование всех трех культур привело бы к увеличению выигрыша на 963 155 иранских риалов на гектар. Эти результаты соответствуют Deng и др. [25] и Falsafian и др. [18], предполагая, что участие в программе комплексного страхования фермы улучшает благосостояние фермеров. Они также согласуются с Adhikari и др. [22], которые продемонстрировали, что правильное управление программами страхования урожая может улучшить эквивалент определенности. Более того, эти результаты сопоставимы с результатами, сообщенными Serfilippi и др. [50] для хлопкоробов в Буркина-Фасо, Ye и др. [51] относительно благосостояния производителей пшеницы в Китае, Gallenstein и Dougherty [52] в Гане, Wang и др. [37] в Китае и Chattha [53] в округе Арканзас в США. Дополнительно, это улучшение благосостояния производителя иллюстрирует экономические выгоды, связанные с политикой WFI, и стратегическую согласованность, которую она создает в управлении рисками для различных сельскохозяйственных результатов. Интегрируя страхование нескольких культур в единую структуру, фермеры могут эффективно смягчать финансовые неопределенности, возникающие из-за неблагоприятных погодных условий, вспышек болезней и рыночных колебаний. Этот коллективный подход способствует созданию среды, где производители поощряются инвестировать в более устойчивые методы земледелия, зная, что их средства к существованию защищены от потенциальных потерь. Более того, эффективность политики WFI приводит к более низким административным затратам и упрощенным процессам по сравнению с управлением отдельными страховыми полисами для отдельных культур. Такое упрощение снижает бюрократическую нагрузку на фермеров, позволяя им больше сосредотачиваться на повышении производительности, а не на навигации по сложным страховым претензиям. Значительное увеличение на 963 155 иранских риалов на гектар не только повышает немедленный доход, но и способствует общей устойчивости сельскохозяйственного сектора, обеспечивая готовность фермеров реагировать на будущие вызовы.
6. Выводы
Это исследование имело две цели: во-первых, определить тариф премии комплексного страхования дохода фермы, а затем рассчитать выгоды для благосостояния производителей от WFI. Параметрические и непараметрические подходы, а также методы, интегрирующие индивидуальные и региональные данные, использовались для оценки программы комплексного страхования дохода фермы. В параметрическом подходе детрендированные урожайности и детрендированные реальные цены использовались для моделирования распределений урожайности и цен соответственно. Функции распределения бета, гамма, нормальное, логнормальное, лог-логистическое, логистическое и Вейбулла использовались для моделирования урожайностей и цен. Расчет CDDFEV для вышеуказанных распределений показал, что бета-функция распределения является наилучшим описанием для урожайностей пшеницы, ячменя и люцерны и цен на пшеницу и люцерну, а лог-логистическая функция была признана подходящей для описания цен на ячмень.
В этом исследовании урожайности репрезентативных ферм были проанализированы с использованием взаимосвязи между урожайностями отдельных фермеров и региональными урожайностями. Для этой цели были рассчитаны отклонения между урожайностями фермеров и средними региональными урожайностями, а затем функция распределения вероятностей индивидуальной урожайности была оценена с использованием двумерной ядерной функции. Результаты, полученные для тарифов страховых премий из симуляции репрезентативных ферм, отличались от результатов параметрических и непараметрических методов. Этот метод также подтвердил, что значения тарифов страховых премий и вероятности убытка в программе страхования двух продуктов были ниже, чем в программах с одним продуктом и тремя продуктами. Другими словами, программа комплексного страхования фермы становится более эффективной, когда количество застрахованных культур увеличивается. Например, при покрытии 75%, вероятности убытка для пшеницы, ячменя и люцерны составляют 63%, 14% и 38% соответственно. В то же время, совместное страхование пшеницы и ячменя снижает вероятность убытка на 39%, страхование пшеницы и люцерны снижает ее на 35%, а страхование ячменя и люцерны уменьшает ее на 7%. В случае страхования всех трех продуктов эта цифра упала до 18%.
В целом, можно заключить, что комплексное страхование дохода фермы с использованием метода двумерной ядерной функции распределения вероятностей будет давать более разумные премии. Поэтому мы рекомендуем применять этот метод для оценки страховых премий. Опыт развитых стран в области сельскохозяйственного страхования, включая США и Индию, показывает, что переход от страхования урожайности к индексному страхованию устранил большинство проблем и минимизировал риск убытка для фермеров и сельскохозяйственного сектора в целом. Поэтому, основываясь на этом вопросе и результатах текущего исследования, рекомендуется, чтобы Фонд сельскохозяйственного страхования применял эту политику вместо традиционной страховой программы. Важный момент в этом контексте заключается в том, что в сельскохозяйственном страховании также необходимо учитывать потребности застрахованных фермеров. Поскольку комплексное страхование фермы имеет более низкие премии, оно может стимулировать фермеров к участию в программах сельскохозяйственного страхования. Следовательно, эта страховая программа должна быть включена в повестку дня Фонда сельскохозяйственного страхования.
В этом исследовании для оценки изменения экономического благосостояния фермеров после их участия в программе комплексного страхования фермы использовался эквивалент определенности путем расчета функции ожидаемой полезности и коэффициентов неприятия риска фермеров. Результаты показали, что, в целом, применение комплексного страхования фермы на различных уровнях увеличивает благосостояние производителей, и, увеличивая уровень покрытия, скорость увеличения благосостояния фермеров также увеличивается. Другими словами, экономическое благосостояние фермера увеличивается, когда он использует страховую программу как минимум для одного продукта, по сравнению со случаем отсутствия страхования. Очевидно, что комплексное страхование фермы может дополнять существующие инструменты управления сельскохозяйственными рисками, и благодаря своим преимуществам оно окажет положительное влияние на развитие застрахованных ферм в Иране, а также на укрепление доверия между фермерами и Фондом сельскохозяйственного страхования. Будущие исследования должны быть сосредоточены на включении производственных затрат в расчеты премий.
Следует отметить, что это исследование имело три ограничения. Во-первых, данные об урожайности на уровне фермы были недоступны за более длительные периоды времени, что могло привести к смещению при измерении корреляции между урожайностью на уровне округа и на уровне фермы. Во-вторых, данные об урожайности на уровне фермы были доступны только для нескольких регионов, что заставило нас сосредоточиться на провинции Зенджан. В-третьих, это исследование было сосредоточено исключительно на доходе фермы, исключая производственные затраты. Будущие исследования, включающие производственные затраты, должны учитывать чистый доход ферм.
Ссылки
1. Skees, J.R.; Barnett, B.J.; Murphy, A.G. Creating insurance markets for natural disaster risk in lower income countries: The potential role for securitization. Agric. Financ. Rev. 2008, 68, 151–167. [Google Scholar] [CrossRef]
2. Nelson, C.H.; Loehman, E.T. Further toward a theory of agricultural insurance. Am. J. Agric. Econ. 1987, 69, 523–531. [Google Scholar] [CrossRef]
3. AIF. Agricultural Insurance Fund; Ministry of Agricultural Jihad: Tehran, Iran, 2020.
4. Coble, K.H.; Knight, T.O.; Goodwin, B.K.; Miller, M.F.; Rejesus, R.M. A Comprehensive Review of the RMA APH and COMBO Rating Methodology: Final Report; Sumaria Systems for the Risk Management Agency: Washington, DC, USA, 2010. [Google Scholar]
5. Turvey, C.G. Whole-farm income insurance in a Canadian context. In Proceedings of the AAEA, CAES, and WAEA Joint Meeting, Denver, CO, USA, 25–27 July 2010. [Google Scholar]
6. Zhu, Y.; Ghosh, S.J.; Goodwin, B.K. Modeling dependence in the design of whole-farm insurance contract: A copula based model approach. In Proceedings of the American Agricultural Economics Association Annual Meeting, Orlando, FL, USA, 27–29 July 2008. [Google Scholar]
7. Hennessy, D.A.; Babcock, B.A.; Hayes, D. The budgetary and producer welfare effects of revenue insurance. Am. J. Agric. Econ. 1997, 79, 1024–1034. [Google Scholar] [CrossRef]
8. Kokot, Z.; Markovic, T.; Ivanovic, S.; Meseldzi, M. Whole-farm revenue protection as a factor of economic stability in crop production. Sustainability 2020, 12, 6349. [Google Scholar] [CrossRef]
9. Meuwissen, M.P.M.; Skees, J.R.; Black, J.R.; Huirne, R.B.M.; Dijkhuizen, A.A. An analytical framework for discussing farm business interruption insurance for classical swine fever. In Proceedings of the AAEA Annual Meeting, Tampa, FL, USA, 30 July–2 August 2000. [Google Scholar]
10. Berg, E. Assessing the farm level impacts of yield and revenue insurance: An expected value-variance approach. In Proceedings of the Xth Congress of the European Association of Agricultural Economists (EAAE), Zaragoza, Spain, 28–31 August 2002. [Google Scholar]
11. Hart, C.E.; Hayes, D.J.; Babcock, B.A. Insuring eggs in baskets: Should the government insure individual risks? Can. J. Agric. Econ. 2006, 54, 121–137. [Google Scholar] [CrossRef][Green Version]
12. Bielza, M.; Garrido, A. Evaluating the potential of whole-farm insurance over crop-specific insurance policies. Span. J. Agric. Res. 2009, 7, 3–11. [Google Scholar] [CrossRef]
13. Coble, K.H.; Chalise, L.; Barnett, B.J.; Miller, J.C. Developing a feasible whole-farm insurance product. In Proceedings of the 2nd International Agricultural Risk, Finance and Insurance Conference (IARFIC), Vancouver, BC, Canada, 16–18 June 2013. [Google Scholar]
14. Chalise, L.; Coble, K.H.; Barnett, J.B.; Miller, J.C. Developing area-triggered whole-farm revenue insurance. J. Agric. Resour. Econ. 2017, 42, 27–44. [Google Scholar]
15. Marković, T.; Kokot, Z. Whole-farm revenue insurance as a new model of risk management in agriculture. Ratar. Povrt. 2018, 55, 22–28. [Google Scholar] [CrossRef]
16. Luckstead, J.; Devadoss, S. Implications of commodity programs and crop insurance policies for wheat producers. J. Agric. Appl. Econ. 2019, 51, 267–285. [Google Scholar] [CrossRef]
17. Biram, H.D.; Coble, K.H.; Harri, A.; Park, E.; Tack, J. Mitigating price and yield risk using revenue protection and agriculture risk coverage. J. Agric. Appl. Econ. 2022, 54, 319–333. [Google Scholar] [CrossRef]
18. Falsafian, A.; Ghahremanzadeh, M.; Aref Eshghi, T.; Rasooli Sharabiani, V.; Szymanek, M.; Dziwulska-Hunek, A. Producer welfare benefits of rating area yield crop insurance. Agriculture 2024, 14, 1512. [Google Scholar] [CrossRef]
19. Goodwin, B.K.; Mahul, O. Risk modeling concepts relating to the design and rating of agricultural insurance contracts. In World Bank Policy Research Working Paper; World Bank: Washington, DC, USA, 2004; Volume 3392. [Google Scholar]
20. Zhu, Y.; Goodwin, B.K.; Ghosh, S.K. Modeling yield risk under technological change: Dynamic yield distributions and the US crop insurance program. J. Agric. Resour. Econ. 2011, 36, 192–210. [Google Scholar]
21. Ozaki, V.A.; Goodwin, B.K.; Shirota, R. Parametric and nonparametric statistical modeling of crop yield: Implications for pricing crop insurance contracts. Appl. Econ. 2008, 40, 1151–1164. [Google Scholar] [CrossRef]
22. Adhikari, S.; Knight, T.O.; Belasco, E.J. Evaluation of crop insurance yield guarantees and producer welfare with upward-trending yields. Agric. Econ. Res. Rev. 2012, 41, 367–376. [Google Scholar] [CrossRef]
23. Lu, Y.; Ramirez, O.A.; Rejesus, R.M.; Knight, T.O.; Sherrick, B.J. Empirically evaluating the flexibility of the Johnson family of distributions: A crop insurance application. Agric. Resour. Econ. Rev. 2008, 37, 79–91. [Google Scholar] [CrossRef]
24. Ramirez, O.A.; Misra, S.; Field, J. Crop-yield distributions revisited. Am. J. Agric. Econ. 2003, 85, 108–120. [Google Scholar] [CrossRef]
25. Deng, X.; Barnett, B.J.; Hoogenboom, G.; Yu, Y.; Garcia, Y. Alternative crop insurance indexes. J. Agric. Appl. Econ. 2008, 40, 223–237. [Google Scholar] [CrossRef]
26. Vedenov, D.V.; Barnett, B.J. Efficiency of weather derivatives as primary crop insurance instruments. J. Agric. Resour. Econ. 2004, 29, 387–403. [Google Scholar]
27. Harri, A.; Coble, K.H.; Ker, A.P.; Goodwin, B.K. Relaxing heteroscedasticity assumptions in area-yield crop insurance rating. Am. J. Agric. Econ. 2011, 93, 703–713. [Google Scholar] [CrossRef]
28. Ker, A.P. Rating and Yield Predicting Procedures for the Group Risk Federal Crop Insurance Program: A Nonparametric Approach. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 1996. [Google Scholar]
29. Goodwin, B.K.; Ker, A.P. Nonparametric estimation of crop yield distributions: Implications for rating group-risk crop insurance contracts. Am. J. Agric. Econ. 1998, 80, 139–153. [Google Scholar] [CrossRef]
30. Ker, A.P.; Goodwin, B.K. Nonparametric estimation of crop insurance rates revisited. Am. J. Agric. Econ. 2000, 82, 463–478. [Google Scholar] [CrossRef]
31. Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. Ser. B Stat. Methodol. 1964, 26, 211–252. [Google Scholar] [CrossRef]
32. Goodwin, B.K.; Ker, A. A comprehensive assessment of the role of risk in US agriculture. Am. J. Agric. Econ. 2002, 85, 291–304. [Google Scholar]
33. Turvey, C.; Zhao, J. Parametric and Non-Parametric Crop Yield Distributions and Their Effects on All-Risk Crop Insurance Premiums; Working Paper WP99/05; Department of Agricultural Economics and Business, University of Guelph: Guelph, ON, Canada, 1999; pp. 1–23. [Google Scholar]
34. Wang, H.H.; Hanson, S.D.; Myers, R.J.; Black, J.R. The effects of crop yield insurance designs on farmer participation and welfare. Am. J. Agric. Econ. 1998, 80, 806–820. [Google Scholar] [CrossRef]
35. Coble, K.H.; Heifner, R.G.; Zuniga, M. Implications of crop yield and revenue insurance for producer hedging. J. Agric. Resour. Econ. 2000, 25, 432–452. [Google Scholar]
36. Lin, C.Y. An economic analysis of alternative rice insurance policies in Taiwan. Taiwan. Agric. Econ. Rev. 2001, 6, 235–253. [Google Scholar]
37. Wang, K.; Zhang, Q.; Kimura, S.; Akter, S. Is the crop insurance program effective in China? Evidence from farmers’ analysis in five provinces. J. Integr. Agric. 2015, 14, 2109–2120. [Google Scholar] [CrossRef]
38. Vedenov, D.V.; Power, G.J. Risk reducing effectiveness of revenue versus yield insurance in the presence of government payment. J. Agric. Appl. Econ. 2008, 40, 443–459. [Google Scholar] [CrossRef]
39. Power, G.J.; Vedenov, D.V.; Hong, S.W. The impact of the Average Crop Revenue Election (ACRE) program on the effectiveness of crop insurance. Agric. Financ. Rev. 2009, 69, 330–345. [Google Scholar] [CrossRef]
40. Wang, Y.; Barnett, B.J.; Coble, K.H.; Harri, A. Yield aggregation impacts on a deep loss systemic risk protection program. In Proceedings of the Agricultural and Applied Economics Association Annual Meeting, Seattle, WA, USA, 12–14 August 2012. [Google Scholar]
41. Dismukes, R.; Coble, K.H.; Miller, C.; O’Donoghue, E. The effects of area-based revenue protection on producers’ choices of farm-level revenue insurance. In Proceedings of the Agricultural and Applied Economics Association 2013 Annual Meeting, Washington, DC, USA, 4–6 August 2013. [Google Scholar]
42. Bulut, H.; Collins, K.J. Designing farm supplemental revenue coverage options on top of crop insurance coverage. Agric. Financ. Rev. 2014, 74, 397–426. [Google Scholar] [CrossRef]
43. Luitel, K.P.; Hudson, D.; Knight, T. Implications and evaluation of crop insurance choices for cotton farmers under the 2014 farm bill. J. Agric. Appl. Econ. 2018, 50, 526–543. [Google Scholar] [CrossRef]
44. Zanjan Provincial Statistical Yearbook. 2021. Available online: https://amar.mpo-zn.ir (accessed on 14 August 2021).
45. Agricultural Jihad Organization of Zanjan Province. Agricultural Statistics, Programming and Economic Affairs Deputy, Ministry of Agriculture-Jihad. 2016. Available online: https://zanjan.maj.ir (accessed on 9 April 2020).
46. Ministry of Agriculture-Jihad. 2021. Available online: https://dpe.maj.ir/amar (accessed on 26 March 2022).
47. Yonar, A.; Yonar, H.; Mishra, P.; Kumarim, B.; Abotaleb, M.; Badr, A. Modeling and forecasting of wheat of South Asian region countries and role in food security. Adv. Comput. Intell. 2021, 1, 11. [Google Scholar] [CrossRef]
48. Kumar, L.; Mishra, P.; Singh, R.B.; Sayyed, M.; Rathi, D.; Srivastava, A.B. Forecasting of area, production and productivity of wheat crop in Madhya Pradesh. Indian J. Econ. Dev. 2022, 18, 577–586. [Google Scholar]
49. Chen, S.L.; Miranda, M.J. Modeling Texas dryland cotton yields, with application to crop insurance actuarial rating. J. Agric. Appl. Econ. 2008, 40, 239–252. [Google Scholar] [CrossRef]
50. Serfilippi, E.; Carter, M.; Guirkinger, C. Insurance contracts when individuals “greatly value” certainty: Results from a field experiment in Burkina Faso. J. Econ. Behav. Organ. 2020, 180, 731–743. [Google Scholar] [CrossRef]
51. Ye, T.; Hu, W.; Barnett, B.J.; Wang, J.; Gao, Y. Area yield index insurance or farm yield crop insurance? Chinese perspectives on farmers’ welfare and government subsidy effectiveness. J. Agric. Econ. 2020, 71, 144–164. [Google Scholar] [CrossRef]
52. Gallenstein, R.A.; Dougherty, J.P. Can revenue index insurance outperform yield index insurance? Am. J. Agric. Econ. 2024, 106, 1648–1683. [Google Scholar] [CrossRef]
53. Chattha, K. Evaluating Margin Protection (MP) Crop Insurance as a Risk Management Tool for Rice Producers in Arkansas. Master’s Thesis, Agricultural Economics, University of Arkansas, Fayetteville, AR, USA, 2024. Available online: https://scholarworks.uark.edu/etd/5391 (accessed on 30 December 2024).
Ahmadabadi MA, Ghahremanzadeh M, Dashti G, Hosseini-Yekani S-A. Evaluating Producer Welfare Benefits of Whole-Farm Revenue Insurance. Agriculture. 2025; 15(2):188. https://doi.org/10.3390/agriculture15020188
Перевод статьи «Evaluating Producer Welfare Benefits of Whole-Farm Revenue Insurance» авторов Ahmadabadi MA, Ghahremanzadeh M, Dashti G, Hosseini-Yekani S-A., оригинал доступен по ссылке. Лицензия: CC BY. Изменения: переведено на русский язык
Фото: freepik
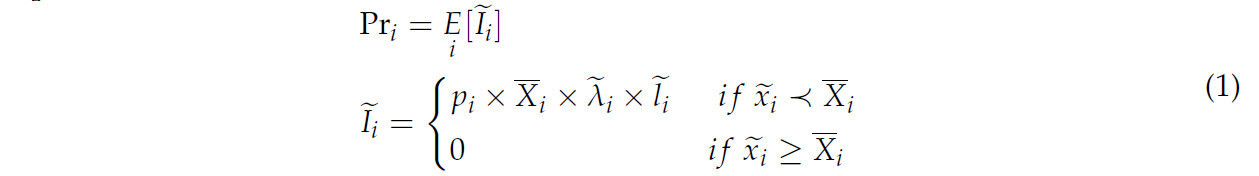
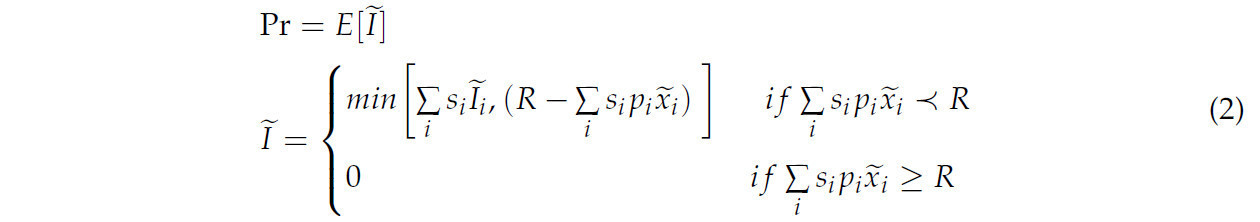
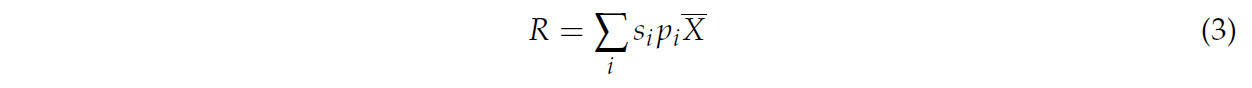


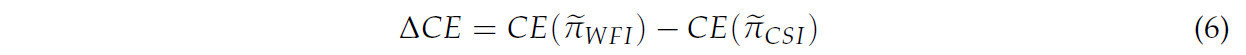
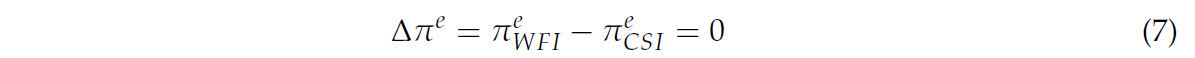
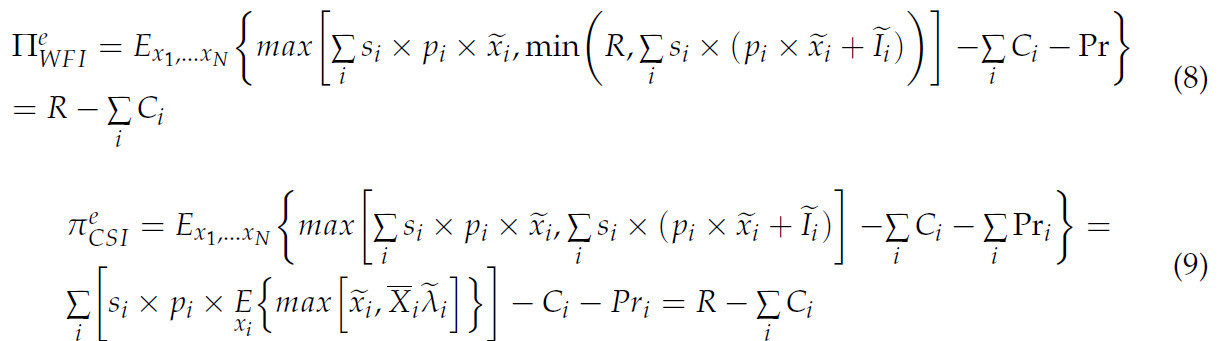
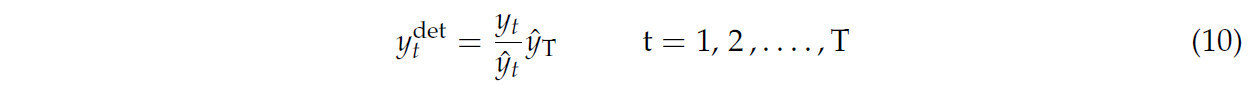
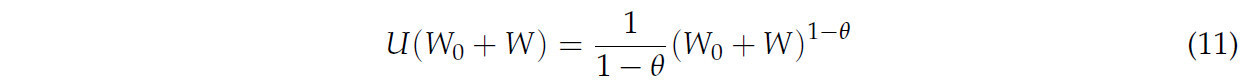
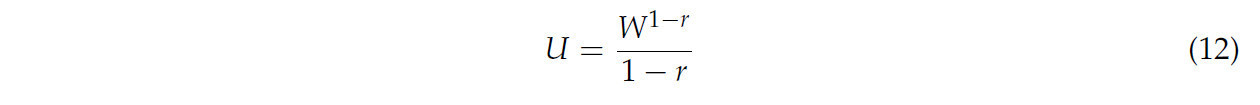
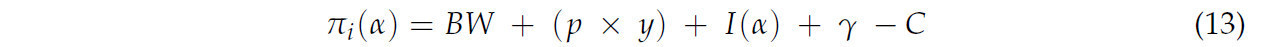
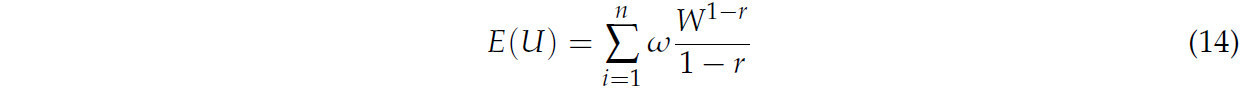
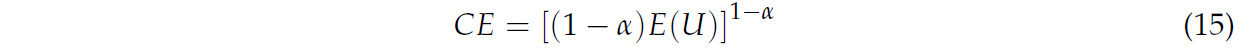

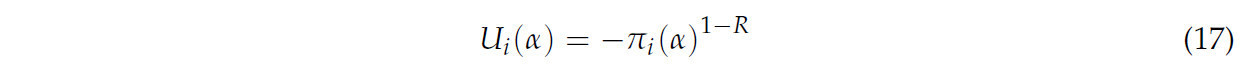
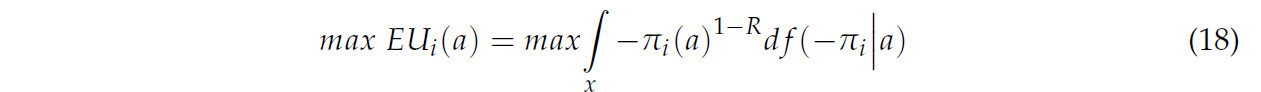
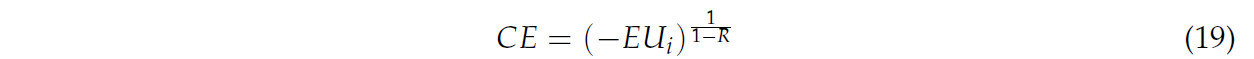


































































































Комментарии (0)