Простой способ предсказания нитратов в воде для орошения на основе искусственного интеллекта

В данном исследовании разработана модель на основе искусственной нейронной сети (ИНС) для прогнозирования концентрации нитратов в дренажных водах с использованием параметров, которые проще и экономичнее измерять, на примере Нижнего бассейна реки Сейхан — ключевого сельскохозяйственного региона Турции. Для этой цели в течение 2022 и 2023 водных лет ежедневно отбирались пробы воды на дренажной измерительной станции, а концентрация нитратов определялась в лаборатории. Параллельно с концентрацией нитратов измерялись и другие параметры, такие как расход воды, электропроводность (EC), pH и количество осадков.

Сложная взаимосвязь между измеренными значениями нитратов и другими, более простыми и менее затратными в измерении параметрами, была использована в двух различных сценариях на этапе обучения модели ИНС-Нитрат. После обучения модели значения нитратов были оценены для обоих сценариев, используя только другие параметры. В Сценарии I прогнозировались случайные значения из набора данных, тогда как в Сценарии II прогноз выполнялся в виде временного ряда. Для обоих сценариев результаты модели сравнивались с измеренными значениями.

Предложенная модель надежно заполняет пробелы в наборах данных (Сценарий I) и прогнозирует значения нитратов во временных рядах (Сценарий II). Несмотря на то, что модель основана на искусственной нейронной сети (ИНС), она также обладает потенциалом для адаптации к другим методам машинного обучения и искусственного интеллекта, таким как метод опорных векторов, деревья решений, случайные леса и методы ансамблевого обучения.

Мониторинг качества воды необходим для поддержания естественных водных объектов и обеспечения чистой питьевой воды. Многочисленные факторы привели к рутинному измерению различных показателей качества воды в реках, озерах и подземных водах, включая нитраты (NO₃), уровни pH, растворенный кислород и другие. Эти переменные помогают отслеживать состояние водных экосистем, выявлять потенциальные источники загрязнения и разрабатывать планы по смягчению последствий. Из них концентрации нитратов особенно важны, потому что высокие уровни в естественных водотоках могут привести к эвтрофикации, которая снижает уровень кислорода и негативно влияет на водную жизнь. Нитраты присутствуют как в поверхностных, так и в подземных водах вследствие естественных процессов и антропогенной деятельности. Основными причинами появления нитратов в поверхностных и подземных водах являются разлагающиеся растительные и животные отходы, определенные категории твердых отходов, бытовые отходы, сточные воды промышленных процессов, сельскохозяйственные удобрения и сточные воды с очистных сооружений [1,2,3].

Повышенные концентрации нитратов в сточных водах указывают как на дефицит основных азотных удобрений, так и на снижение эффективности производства. Поэтому крайне важно отслеживать перемещение нитратного азота в сочетании с интенсивными методами сельскохозяйственного и животноводческого производства. Использование нейронных сетей представляет собой перспективный инновационный инструмент для точного моделирования сложной динамики азота в искусственно дренированных почвах [4]. Из-за своего воздействия на качество воды и целостность экосистемы загрязнение нитратами в мелких подземных водах и естественных водоемах создает серьезные проблемы для управления окружающей средой и общественного здравоохранения. Непрерывный отбор проб с течением времени для мониторинга уровня нитратов предоставляет ключевое понимание тенденций загрязнения и информирует о стратегиях восстановления. Однако пробелы часто появляются в этих наборах данных по разным причинам, включая технические ограничения или ошибки обработки данных, что требует точных методов для заполнения отсутствующих значений с целью сохранения целостности данных и качества последующего анализа. Отсутствующие значения в этих наборах данных временных рядов усложняют анализ данных, поскольку они могут искажать статистические результаты и затруднять создание надежных планов управления водными ресурсами. Для сохранения целостности долгосрочных наборов данных мониторинга необходимы точные методы импутации отсутствующих значений.

Значительные пробелы в данных и ограниченный публичный доступ в некоторых районах характеризуют неадекватность глобальных баз данных о качестве подземных вод [5,6,7]. Защита экологической целостности и общественного здоровья требует активизации исследований и мониторинга качества подземных вод [8,9,10,11].

Ряд факторов, включая неисправности оборудования, проблемы с отбором проб или внешние обстоятельства, которые могут сделать регулярный сбор данных невозможным, могут привести к отсутствию наборов данных о качестве воды. Мониторинг процессов качества воды и характеристика загрязняющих веществ связаны со значительными финансовыми и трудовыми затратами, требующими обширных инициатив по отбору проб и сложного лабораторного тестирования. Поэтому текущие усилия сосредоточены на разработке новых инноваций, направленных на повышение практичности этих усилий. Из-за взаимодействий и корреляций между параметрами качества воды, такими как концентрации анионов и катионов, уместно изучить, существует ли специфический для области механизм, управляющий наблюдаемыми закономерностями, тем самым подтверждая предсказуемость этих параметров. Обнаружение таких прогностических моделей имеет особое значение для экологов и специалистов в области наук об окружающей среде, поскольку оно дает им возможность прогнозировать уровни загрязнения воды и заблаговременно применять необходимые превентивные меры [12,13].

Значительный прогресс в применении машинного обучения улучшил способность прогнозировать наличие таких загрязняющих веществ, как фторид, нитраты и мышьяк [14,15,16,17]. Тем не менее, продолжающийся сброс опасных веществ в результате деятельности человека по-прежнему создает новые риски, что требует изменения подходов к исследованиям [18,19]. Чтобы гарантировать устойчивое управление водными ресурсами, необходимы конкретные меры для поддержания качества водных ресурсов в разумных и осуществимых пределах при удовлетворении спроса. Таким образом, крайне важно понимать, как ведут себя системы загрязнитель-вода и как NO₃ переносится в точку, где можно предсказать, как он будет реагировать на различные изменения. При отсутствии гидрогеологической базы данных метод искусственного интеллекта можно обучить с использованием данных из множества источников разных масштабов для решения и прогнозирования сложных процессов [20].

В последнее время стохастические методы моделирования, такие как искусственные нейронные сети (ИНС), помимо используемых в обработке изображений (например, сверточные нейронные сети), привлекли значительный научный интерес благодаря своей простоте, быстрым вычислительным возможностям и относительной эффективности по сравнению с детерминированными моделями [21,22]. Для сохранения целостности долгосрочных наборов данных мониторинга необходимы точные методы импутации отсутствующих значений. В этой ситуации полезны методы прогнозного моделирования, такие как ИНС. Основная задача заключается в обучении модели для точного предсказания отсутствующих точек, особенно когда пробелы в данных велики или когда они включают критические сезонные колебания. Поскольку нитраты считаются основным показателем для оценки загрязнения подземных вод из-за отходов животноводческих ферм или другой сельскохозяйственной деятельности, важно тщательно отслеживать концентрации нитратного азота (NO₃-N) как в поверхностных подземных водах, так и в подповерхностном стоке. Выщелачивание нитратов с сельскохозяйственных полей, получающих навоз и удобрения, как правило, заметно выше в дренажных водах подповерхностного стока, чем в поверхностном стоке [23].

В науках об окружающей среде и гидрологии ИНС являются эффективными инструментами для прогнозирования отсутствующих значений в данных временных рядов. Вдохновленные нейронной архитектурой человеческого мозга, ИНС особенно хорошо подходят для прогнозирования отсутствующих уровней нитратов, поскольку они могут улавливать множество нелинейных корреляций в наборах данных об окружающей среде. ИНС способны изучать закономерности и тенденции по предыдущим показаниям нитратов и связанным с ними экологическим переменным, что помогает им прогнозировать отсутствующие значения с высокой степенью точности. Одним из главных преимуществ ИНС является их способность извлекать знания из неполных наборов данных. При соответствующем обучении ИНС обладают способностью «обобщать» на основе распознанных закономерностей в доступных данных, чтобы экстраполировать отсутствующие значения. В этом контексте входные переменные, подаваемые в ИНС, включают исторические концентрации нитратов, метеорологические данные и, возможно, другие экологические показатели. Интегрируя информацию из этих входных данных, ИНС предсказывает отсутствующие концентрации нитратов во временной последовательности.

Оценка концентраций нитратов с использованием экономически эффективных технологий имеет важное значение. Модели «черного ящика», такие как ИНС, вызывают большой интерес в прогнозировании концентрации нитратов с использованием легко измеряемых параметров качества воды, таких как температура, электропроводность (ЕС), уровень подземных вод и pH. В этом контексте ИНС не требуют предварительных знаний о структуре и возможных взаимосвязях между значимыми переменными. Кроме того, присущие ИНС возможности обучения привели к их способности адаптироваться к системным изменениям [24]. ИНС используются для моделирования сложных процессов, распознавания образов и выполнения анализа временных рядов в различных научных дисциплинах, включая, помимо прочего, финансовые и экономические исследования, исследования в области промышленного инжиниринга, гидрологические исследования, метеорологический анализ и усилия в области агроэкологических исследований [25,26,27,28,29,30,31,32]. Стаменкович [33] работал над исследованием, касающимся прогнозирования концентраций питательных веществ в речных системах в национальном масштабе, применяя два различных метода искусственного интеллекта. Методы искусственных нейронных сетей (ИНС) и машин опорных векторов (SVM) использовались для оценки годовых концентраций нитратов и фосфатов в реках одиннадцати европейских стран в этом исследовании. Полученные результаты указывают, что модель ИНС демонстрирует превосходящую эффективность в прогнозировании концентраций нитратов и фосфатов по сравнению с моделями SVM. Такие результаты подчеркивают, что модель ИНС представляет собой потенциально выгодный инструмент для предсказания уровней питательных веществ в речных системах. Стаменкович и др. [34] использовали многослойную модель ИНС для прогнозирования концентраций нитратов в реке Дунай на территории Сербии, используя данные о качестве воды, наблюдаемые на десяти мониторинговых станциях в период с 2011 по 2016 год. Анализ корреляции Пирсона и фактор инфляции дисперсии использовались для решения, какие из измеренных параметров следует использовать для определения входных данных модели. Согласно корреляционному анализу, 7 параметров были выбраны в качестве входных значений, а согласно анализу VIF, 21 параметр был выбран в качестве входных значений. Для обоих случаев количество нейронов в скрытом слое составило 20. Результаты анализа показали, что производительность модели была наивысшей, когда в качестве входных данных было выбрано семь параметров. Значения RMSE, MAE и R² использовались для определения производительности модели и были рассчитаны как 0,68, 0,42 и 0,91 соответственно. Также в аналогичных исследованиях, проведенных по этой теме, несколько исследователей предложили нейронные сети, которые используют переменные водного баланса или показатели качества воды в качестве входных параметров для моделирования загрязнения нитратами [35]. Бэнд и др. [36] смоделировали концентрацию нитратов в подземных водах в бассейне Марвдашт в Иране на основе различных методов искусственного интеллекта, таких как машины опорных векторов (SVM), случайные леса (RF) и байесовские искусственные нейронные сети (Bayesian-ANN). С этой целью уровни нитратов были измерены в 67 скважинах в районе исследования и использованы в качестве зависимых переменных для моделирования. В качестве входных данных модели были выбраны 11 независимых переменных, таких как высота, уклон, плановая кривизна, профильная кривизна, осадки, пьезометрическая глубина, расстояние до реки, расстояние до населенных пунктов, натрий (Na), калий (K) и индекс топографической влажности (TWI), влияющие на изменение нитратов в подземных водах, с учетом матрицы корреляции Пирсона. Указывается, что данные из 67 скважин с измерениями нитратов использовались при моделировании; 70% данных использовались в качестве обучающих данных и 30% — в качестве тестовых данных. Для оценки производительности моделей использовались такие критерии оценки, как коэффициент детерминации (R²), средняя абсолютная ошибка (MAE), среднеквадратическая ошибка (RMSE) и эффективность Нэша-Сатклиффа (NSE). Сообщалось, что модель RF (R² = 0,89, RMSE = 4,24, NSE = 0,87) дает лучшие результаты, чем другие модели. Видно, что производительность моделей довольно хорошая. Однако отсутствие оценки того, являются ли входные и выходные значения одновременными или нет, и отсутствие временного изменения результатов модели составляют недостатки модели. Хрнджица и др. [37] использовали глубокие нейронные сети (DNN) и традиционные искусственные нейронные сети (ИНС) для моделирования и прогнозирования концентрации нитратов в реке Клокот в Боснии и Герцеговине. Измерения NO₃(t), pH(t), NO₃(t-1) и pH(t-1) использовались в качестве входных данных для прогнозирования NO₃(t+1) в качестве выходных данных модели. MSE использовалась в качестве функции оценки ошибки, и в скрытом слое использовалось 64 нейрона. Авторы заявили, что тестовая производительность как сетей DNN, так и ИНС была низкой из-за переобучения обеих моделей. В заключение авторы заявили, что им не удалось точно смоделировать концентрацию нитратов в реке Клокот, но DNN была немного лучше, чем ИНС, с точки зрения точности прогнозирования. Считается, что это связано с очень низкой корреляцией между нитратами и pH и большим количеством нейронов, использованных в модели (64). Это объясняется тем, что известно, что при неправильном выборе архитектуры сети в моделях ИНС тестовая производительность снижается из-за чрезмерного обучения [38]. Другая группа [39] использовала ИНС в качестве модели текущего типа для оценки загрязнения нитратами водоносного горизонта в секторе Газа. Также была представлена более простая модель, использующая pH, температуру, электропроводность и уровень водоносного горизонта в качестве входных параметров [39]. Если доступны длинные временные ряды, нейронные сети можно использовать для долгосрочного прогнозирования концентраций нитратов в подземных водах [3].

В другом исследовании была представлена более простая модель с уровнем водоносного горизонта, pH, температурой и электропроводностью в качестве входных параметров [40]. Нейронные сети можно использовать для прогнозирования концентраций нитратов в подземных водах в течение длительного периода времени, если предоставлены длинные временные ряды [3]. В более позднем исследовании [41] оценивались зоны риска по нитратам путем сравнения методов машинного обучения.

Стилианудаки и др. [42] были направлены на оценку концентрации нитратов (NO₃) в подземных водах с использованием искусственных нейронных сетей (ИНС) с данными, которые можно легко измерить in situ. В исследовании использовались данные химического и физического анализа проб подземных вод, взятых из скважин на равнине Копаид и в бассейне реки Асопос в Греции, и сообщалось, что данные состояли из 112 записей, собранных из шестнадцати скважин с равными интервалами четыре раза в год. Исследование проводилось в двух различных сценариях. Значения корреляции Пирсона учитывались при выборе входных значений, и в первом сценарии легко измеряемые данные, такие как pH, электропроводность, температура воды, температура воздуха и уровень водоносного горизонта, использовались в качестве входных данных для модели. Во втором сценарии к входным данным модели, помимо использованных в Сценарии 1, были добавлены проценты землепользования. Для определения оптимальной сетевой структуры модели применялась процедура проб и ошибок, и оптимальное количество нейронов было выбрано равным 10. В качестве функций активации были выбраны сигмоидная функция активации в скрытом слое и линейная функция активации в выходном слое. Набор данных, использованный на этапах обучения и тестирования, был случайным образом выбран как 80% и 20% от общего объема данных соответственно. Для определения производительности модели использовались меры RMSE и NSE. В то время как для Сценария 1 RMSE = 26,18 и NSE = 0,54, для Сценария 2 RMSE = 15,95 и NSE = 0,70. Другими словами, добавление процентов землепользования к входным значениям привело к заметному улучшению производительности модели. Согласно Мориаси и др. [43], модель считается обладающей хорошей чувствительностью при NSE > 0,65.

Эль Амри и др. [44] разработали модели искусственной нейронной сети (ИНС) и авторегрессионной интегрированной скользящей средней (ARIMA) для определения концентраций нитратов и прогнозирования будущих уровней в мелком водоносном горизонте Махдия-Кссур Эссеф, расположенном в центрально-восточном регионе Туниса. В этом контексте 11 факторов были выбраны в качестве входных значений в качестве основных влияющих факторов, связанных с концентрацией нитратов в водоносном горизонте Махдия-Кссур Эссеф. Этими факторами являются: глубина до уровня грунтовых вод (GT), поголовье скота (L), количество удобрений (AF), землепользование — зерновые (LUC), землепользование — овощные культуры (LUVc), землепользование — оливковые культуры (LUOc), землепользование — кормовые культуры (LUFc), землепользование — плодовые сады (LUO), грубая текстура почвы (SC), средняя текстура почвы (SM) и тонкая текстура почвы (SF). Модель была протестирована для 11 различных конфигураций входных данных с использованием этих факторов, и наилучшие результаты были получены при использовании всех факторов. Оптимальное количество нейронов было определено как семь путем проб и ошибок. Модель ИНС показала хорошее соответствие между измеренными и смоделированными результатами, а значения коэффициента детерминации (R²), среднеквадратической ошибки (RMSE) и средней абсолютной ошибки (MAE) составили 0,88, 53,95 и 39,64 соответственно. Также сообщалось, что результаты ИНС были лучше, чем у модели ARIMA.

Дэн и др. [45] использовали набор данных результатов гидрохимических испытаний 316 проб подземных вод, собранных в период с 2011 по 2015 год в районах интенсивного сельского хозяйства на северо-востоке Китая. Модель прогнозирования искусственной нейронной сети с радиально-базисной функцией (RBF ANN) и модель регрессии главных компонент (PCR) были построены с использованием этого набора данных, а алгоритм оптимизации роя частиц был применен для определения оптимальных комбинаций параметров RBF ANN. Входные значения были выбраны из большого числа основных химических параметров с высокой корреляцией с нитратами. Результаты показали, что модель RBF-ANN предоставляет более высокую точность, но модель PCR обеспечивает лучшую интерпретируемость. Поэтому интеграция этих двух моделей выгодна для исследований по прогнозированию нитратов.

Многочисленные публикации также затрагивают использование моделей ИНС в прогнозировании потери почвы, питательных нагрузок в водотоки, оценке ежедневной эталонной эвапотранспирации и управлении дренажными водами [4,46,47,48,49]. Чау [50] провел всестороннее изучение интеграции и представил достижения, касающиеся внедрения искусственного интеллекта в области моделирования качества воды. Хатзикос и др. [51] использовали нейронные сети, характеризующиеся активными нейронами, в качестве методологического инструмента для прогнозирования параметров качества морской воды, таких как температура, pH, растворенный кислород и мутность. Ваг и др. [52] разработали модель ИНС, способную прогнозировать концентрацию нитратов на основе входных переменных, таких как ЕС, TDS, TH, Mg, Na, Cl, HCO₃ и SO₄. Исследователи использовали различные алгоритмы ИНС для прогнозирования уровней нитратов. Оптимальная модель ИНС состояла из семи и восьми входных нейронов, шести скрытых нейронов и нитратов в качестве выходной переменной в пред- и постмуссонный периоды 2012 года. Они предложили, что нейронные сети являются эффективными инструментами для прогнозирования загрязнения воды.

Латиф и др. [53] разработали и применили трехслойную модель искусственной нейронной сети прямого распространения (ИНС) для прогнозирования нитратов (NO₃), параметра качества воды (WQP), в водохранилище Фэйтсуй (Тайвань). Оптимальное количество нейронов было определено как 17 с помощью процедуры проб и ошибок путем увеличения количества нейронов с 1 до 20. Пять параметров качества воды контролировались и использовались в качестве входных данных для модели: аммоний (NH₃), диоксид азота (NO₂), растворенный кислород (DO), нитраты (NO₃) и фосфаты (PO₄). Коэффициент корреляции (R) использовался в качестве статистической меры для оценки производительности модели, и результаты показали, что ИНС является точной моделью для прогнозирования нитратов как параметра качества воды в водохранилище Фэйтсуй. Значения регрессии для обучения, тестирования, валидации и общие составили 0,92, 0,93, 0,99 и 0,94 соответственно. Тот факт, что значение нитратов, предсказанное предложенной моделью ИНС, также было одним из пяти входных параметров модели, ограничивает надежность и применимость модели.

Мэн и др. [54] объединили алгоритм искусственной нейронной сети (ИНС) и электрохимические методы с методами искусственного интеллекта для прогнозирования и интеллектуального контроля удаления нитратов. Начальная концентрация нитратов, pH, время и плотность тока использовались в качестве входных данных модели, а оптимизированные выходные значения нитратов использовались в качестве выходных данных для максимизации удаления нитратов. В качестве архитектуры сети использовались четыре входных значения, семь нейронов скрытого слоя и одно выходное значение. RMSE использовалась в качестве критерия оценки ошибки. Оптимальное удаление нитратов и снижение энергопотребления были достигнуты путем корректировки входных значений. Поскольку это было прототипное исследование, оно отличается от представленного исследования и других упомянутых исследований, и сходство ограничивается использованием ИНС.

Долгосрочный мониторинг уровней нитратов необходим для отслеживания нагрузки питательных веществ и обеспечения качества воды. Однако пробелы в наборах данных по нитратам, будь то из-за спорадического отбора проб или других проблем, могут иметь серьезные последствия для принятия решений на основе данных при управлении водными ресурсами. В этом исследовании мы оцениваем применение ИНС для прогнозирования отсутствующих уровней нитратов в анализах проб воды, регулярно собираемых из бассейна. Мы применяем ИНС для прогнозирования и заполнения пробелов в одном и том же наборе отсутствующих данных о качестве воды, с упором на концентрации нитратов в пробах воды. Рассматриваются различные сценарии как возможные модели для структурирования ИНС и используются долгосрочные наборы данных за определенные временные ряды, в которые намеренно вставлены пробелы для имитации сценариев неполных данных. В этом контексте сценарии отсутствующих данных моделируются путем намеренного удаления участков набора данных временного ряда по нитратам с последующим использованием ИНС для прогнозирования отсутствующих данных. Чтобы проверить точность прогнозов ИНС, мы сравниваем прогнозируемые значения с фактическими измерениями нитратов, которые были намеренно исключены из набора данных. Этот подход позволяет нам оценить производительность модели ИНС в прогнозировании отсутствующих уровней нитратов с использованием известных достоверных данных, оценивая как точность прогнозов, так и надежность модели в различных экологических контекстах. Дополнительно, еще одним важным вкладом исследования является то, что оно обещает практические последствия для управления водными ресурсами, которое требует много времени, усилий, технической работы и экологического мониторинга. Точное и своевременное прогнозирование концентраций нитратов не только помогает в нашем понимании динамики загрязнения, но также поддерживает процессы принятия решений, направленные на смягчение негативных воздействий на качество воды и здоровье человека.

Всесторонний обзор существующей литературы показывает, что большинство исследований по оценке концентраций нитратов (NO₃) с использованием моделей искусственного интеллекта в основном были сосредоточены на подземных водах, реках и водохранилищах. Эти исследования, как правило, основывались на пробах воды, собранных в различных местах ежемесячно или сезонно. Дополнительно, некоторые исследования затрагивали удаление NO₃ в этих водных системах, хотя эти исследования остаются ограниченными по охвату. Примечательно, что тщательное изучение литературы указывает на отсутствие исследований, непосредственно соответствующих целям нашего исследования, особенно в контексте орошаемого бассейна. В этом отношении наше исследование представляет собой пионерский и новый вклад в эту область. Оно предоставляет практический пример применения методов искусственного интеллекта в реальном орошаемом бассейне, характеризующемся интенсивной сельскохозяйственной деятельностью. В течение двух гидрологических лет (2022–2023 гг.) одновременно и ежедневно отбирались пробы воды из единой точки сброса в пределах бассейна, где регистрируются комплексные данные, связанные с характеристиками бассейна. Эти образцы анализировались в лабораторных условиях для определения концентраций NO₃. Полученные данные впоследствии оценивались с использованием указанной модели искусственной нейронной сети (ИНС). Таким образом, с помощью этого исследования, проверяя прогнозы ИНС по сравнению с фактическими измеренными значениями, мы вносим вклад в повышение надежности и полезности прогностических моделей в исследованиях качества воды. С помощью этого комплексного подхода мы также ставим целью предоставить ценные прогнозы относительно потенциала ИНС для повышения точности и надежности прогнозирования нитратов в естественных водных системах.

2.1. Район исследования, отбор проб воды и анализ

Орошаемый район Акырсу (AID), являющийся районом исследований, расположен на Нижней равнине реки Сейхан (LSP) в Турции, в водосборной площади, простирающейся на 9495 гектаров [55,56]. Этот регион преимущественно имеет ровный, однородный рельеф и средиземноморский климат с жарким, сухим летом и теплой дождливой зимой. AID регистрирует 18,9 °C как среднегодовую температуру воздуха, 9,0 °C как самую низкую и 31,0 °C как самую высокую. Дополнительно, сообщается, что водосбор и его окрестности получают в среднем 649,5 мм годовых осадков [57]. В исследуемом районе в зимний сезон 2022 года в основном выращивали цитрусовые, пшеницу, лук и картофель. В Турции летний сезон обычно длится с 1 июня до конца августа, а зимний сезон обычно длится с 1 декабря до конца февраля. Мелкий уровень грунтовых вод и качество воды этого полузасушливого региона подверглись влиянию продолжительного, непрерывного орошения [57]. Структура почвы исследуемого района в целом тяжелого гранулометрического состава с высоким содержанием глины, а избыточная вода в почве отводится через открытые дренажные каналы. Поэтому постоянное управление качеством воды крайне важно в этой области.

Одиннадцать различных почвенных серий (Инчирлик, Арыклы, Енидже, Иннаплы, Арпаджи, Чанакджи, Мурсель, Исмаилие, Гёльяка, Гемисуре и Миссис) составляют почвы Акырсу [58,59], и 67% всей исследовательской площади покрыты сериями Арыклы (29,5%), Инчирлик (25,3%) и Енидже (12,2%). Мурсель (0,7%) и Иннаплы (1,03%) имеют наименьшее распространение [59]. Нижняя равнина реки Сейхан не является преимущественно карстовой областью, но определенные части региона могут проявлять некоторые карстовые характеристики из-за подстилающих известняковых образований. В исследуемом районе уровни грунтовых вод близки к уровням зоны корней растений, особенно в дождливые сезоны и периоды, когда орошение интенсивное (в среднем 1,5 м). Уровень грунтовых вод в исследуемом районе обычно варьируется между 1,5 и 3 м, с сезонными колебаниями, которые влияют на уровень воды и динамику дренажа. По мере уменьшения интенсивности орошения к концу гидрологического года глубина залегания грунтовых вод начинает опускаться ниже корневой зоны. В конце сезона орошения и в периоды без осадков грунтовые воды могут превышать глубину 2,5 м.

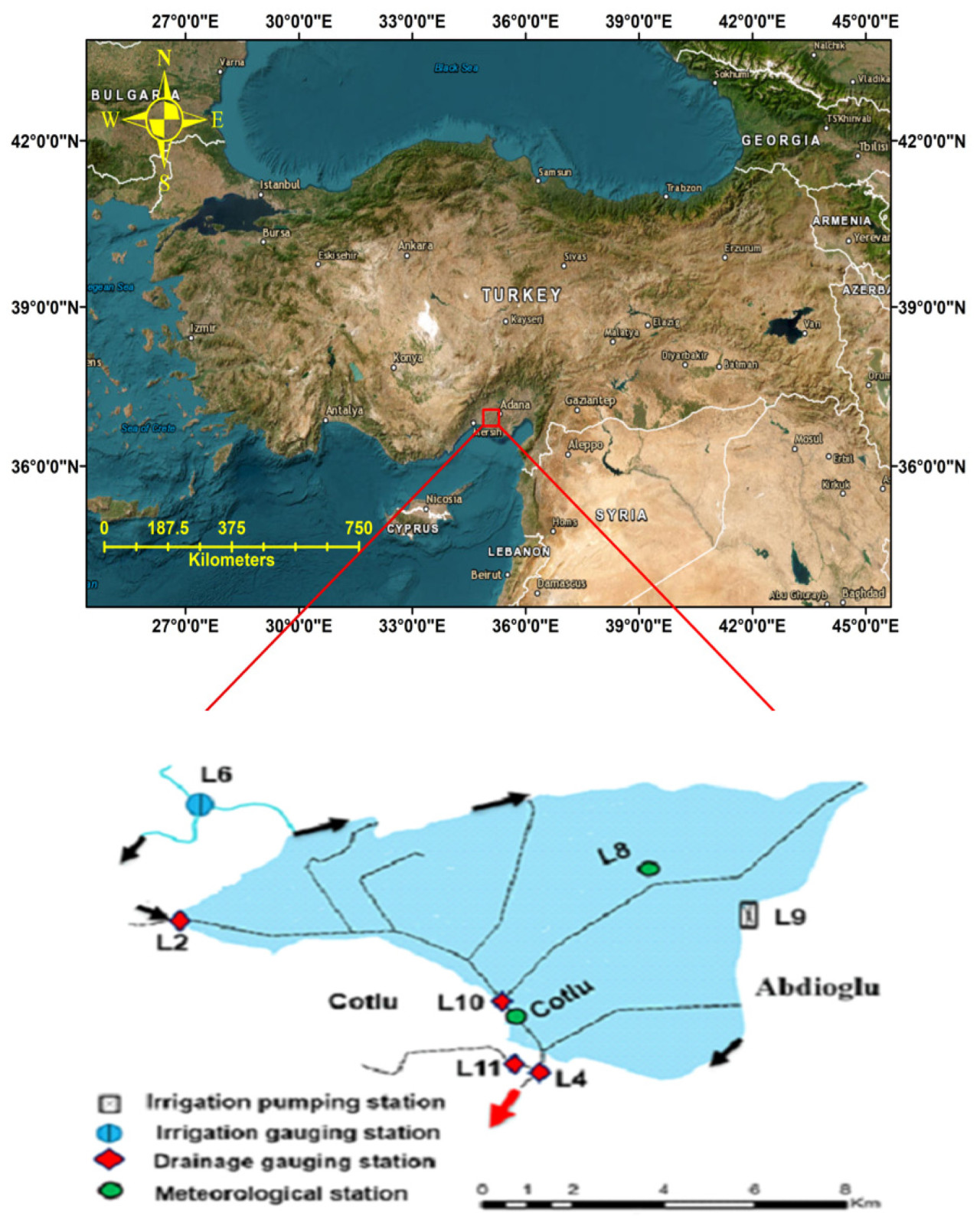
Рисунок 1 показывает AID, который расположен в восточном Средиземноморском регионе Турции. На карте представлен подробный обзор Нижней равнины реки Сейхан в Турции, с акцентом на инфраструктуру орошения и дренажа. Она включает карту, показывающую более широкий регион, и меньшую врезную карту, фокусирующуюся на самой Нижней равнине реки Сейхан. Направления потока, представленные стрелками, указывают направления потока воды для орошения и дренажа в пределах равнины.

Рисунок 1. Местоположение района исследования в Турции, направления потоков оросительной и дренажной воды и станция отбора проб воды (Дренажная измерительная станция).

Нижняя равнина реки Сейхан является сельскохозяйственным районом с хорошо развитой системой орошения и дренажа. Насосные станции получают воду из источника (река, водохранилище) для подачи в оросительные каналы. Измерительные станции помогают контролировать поток воды и обеспечивать эффективное управление системой. Как видно на Рисунке 1, насосная станция орошения используется для перекачки воды на сельскохозяйственные площади; измерительная станция орошения измеряет расход и уровни воды в оросительных каналах. Дренажные станции собирают избыточную воду с полей и отводят ее в подходящий коллектор. Пробы дренажной воды, использованные в исследовании, ежедневно отбирались автоматически с помощью автоматического устройства для отбора проб воды (ISCO-3700, Луисвилл, Кентукки, США), установленного на дренажной измерительной станции, где проводились наблюдения. Пробы воды доставлялись в лабораторию кафедры сельскохозяйственных сооружений и орошения сельскохозяйственного факультета Университета Чукурова для подготовки к анализу и сначала регистрировались в лабораторном журнале, затем фильтровались с помощью фильтровальной бумаги синей ленты и переносились в пластиковые бутылки, очищенные путем пропускания через хромовую кислоту. Бутылки маркировались в соответствии с методикой. В зависимости от времени и трудозатрат, пробы воды либо анализировались немедленно [60], либо хранились в холодильнике при +4 °C до проведения анализа. В анализах, выполненных для определения концентраций NO₃ в оросительных и дренажных водах в единицах мг·л⁻¹, использовался спектрофотометр марки Shimadzu.

2.2. Использованные наблюдательные данные

Набор данных, использованный в модельных исследованиях, был получен путем измерений расхода, проведенных на дренажной измерительной станции, и лабораторных анализов собранных проб воды. Охватывая 2022 и 2023 водные годы, набор данных охватывает 730 дней и включает EC, pH, Q (Расход), P (ежедневные осадки), NO₃ и значение DOWY (день водного года), которое указывает день водного года для каждого дня измерения для учета временных вариаций в наборе данных. Состоящий из 730 строк и 5 столбцов, набор данных использовался в двух сценариях на этапах обучения и тестирования предложенной модели ИНС, причем каждый сценарий содержал свои собственные два различных условия. Подробная информация относительно сценариев предоставлена в разделе 2.3.

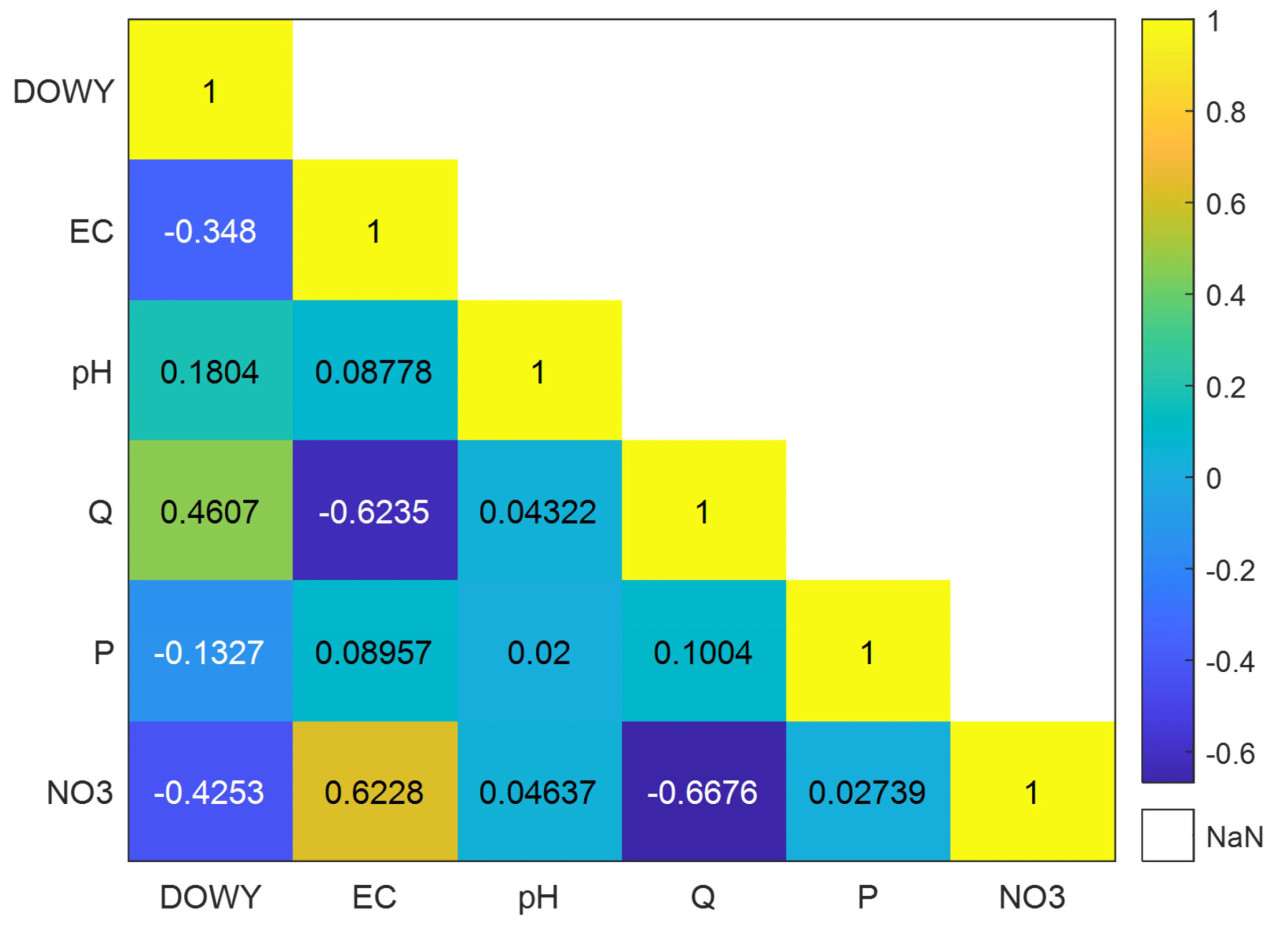
Как упоминалось выше, поскольку измерение нитратов является сложным и дорогостоящим процессом, это исследование ставит целью разработать метод выражения значений нитратов через несколько параметров, которые легче и дешевле измерять, вместо того чтобы полагаться на лабораторные анализы. Для этого процесса, как видно на Рисунке 2, были рассчитаны корреляции между уровнями нитратов и значениями DOWY, EC, pH, Q и P, и самая высокая корреляция с нитратами была найдена обратно пропорциональной расходу (-0,668). За ней последовала корреляция между нитратами и ЕС (0,623). Хотя корреляция между нитратами и другими параметрами была относительно слабой, предварительные тесты указали, что использование этих параметров в качестве входных данных положительно влияет на обобщающую способность и тестовую производительность модели.

Рисунок 2. Корреляционная взаимосвязь между NO₃ и параметрами модели.

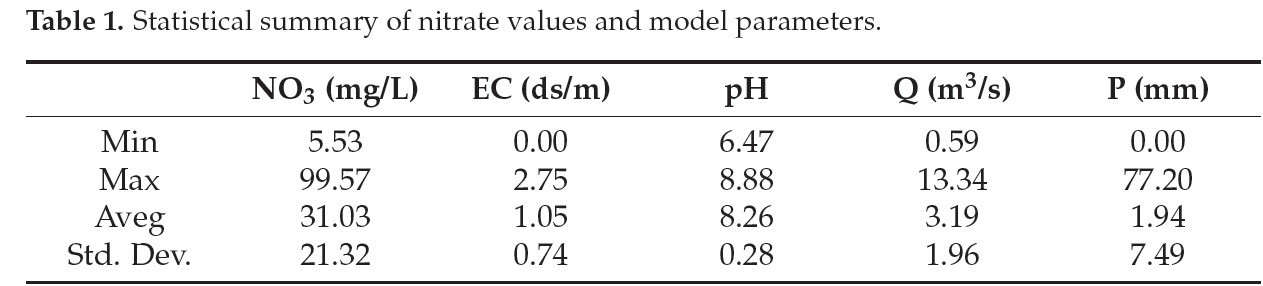
Минимум, максимум, среднее и стандартные отклонения концентраций нитратов и параметров модели суммированы в Таблице 1. Как показано в Таблице 1, средняя концентрация нитратов за два года составила 31,03 мг/л, со стандартным отклонением 21,32 мг/л. Среднесуточный расход, измеренный в дренажном канале, составил 3,19 м³/с со стандартным отклонением 1,96 м³/с. Изменчивость значений осадков и ЕС (электропроводности) также была довольно высокой, что указывает на то, что набор данных, использованный в процессе моделирования, был особенно сложным. Несмотря на это, была достигнута очень хорошая производительность модели. Дополнительно, важно подчеркнуть, что весь набор данных состоял из реальных полевых данных, полученных в результате измерений на месте и лабораторных анализов, что повышает оригинальность и ценность исследования.

Таблица 1. Статистическая сводка значений нитратов и параметров модели.

В матрице корреляций, предоставленной на Рисунке 2, три различные комбинации были использованы в предварительных расчетах для выбора архитектуры сети модели, основанной на корреляционных взаимосвязях между концентрациями нитратов, предназначенными для прогнозирования с использованием предложенной модели, и другими параметрами.

Все данные, использованные в модели, являются оригинальными и основаны на интенсивных полевых и лабораторных измерениях, требующих значительных усилий и времени. В предварительной оценке для моделирования матрица данных была проверена на наличие дублирующих строк, и повторяющиеся данные не были найдены. Значения, которые показывали отклонения на диаграммах рассеяния, не исключались как выбросы. Это связано с тем, что полевые наблюдения показали, что в случаях нехватки вода из дренажных каналов иногда использовалась для орошения, или вода перекачивалась в орошаемую зону в засушливые сезоны для использования в орошении. В целом было установлено, что качество воды, используемой в этих ситуациях, было ниже по сравнению с основным источником воды для орошения. Поэтому сохранение экстремальных значений считалось важным как для будущей разработки моделей, так и для проектирования стратегий управления, которые будут реализованы в полевых условиях. По этой причине такие значения не исключались как выбросы из набора данных.

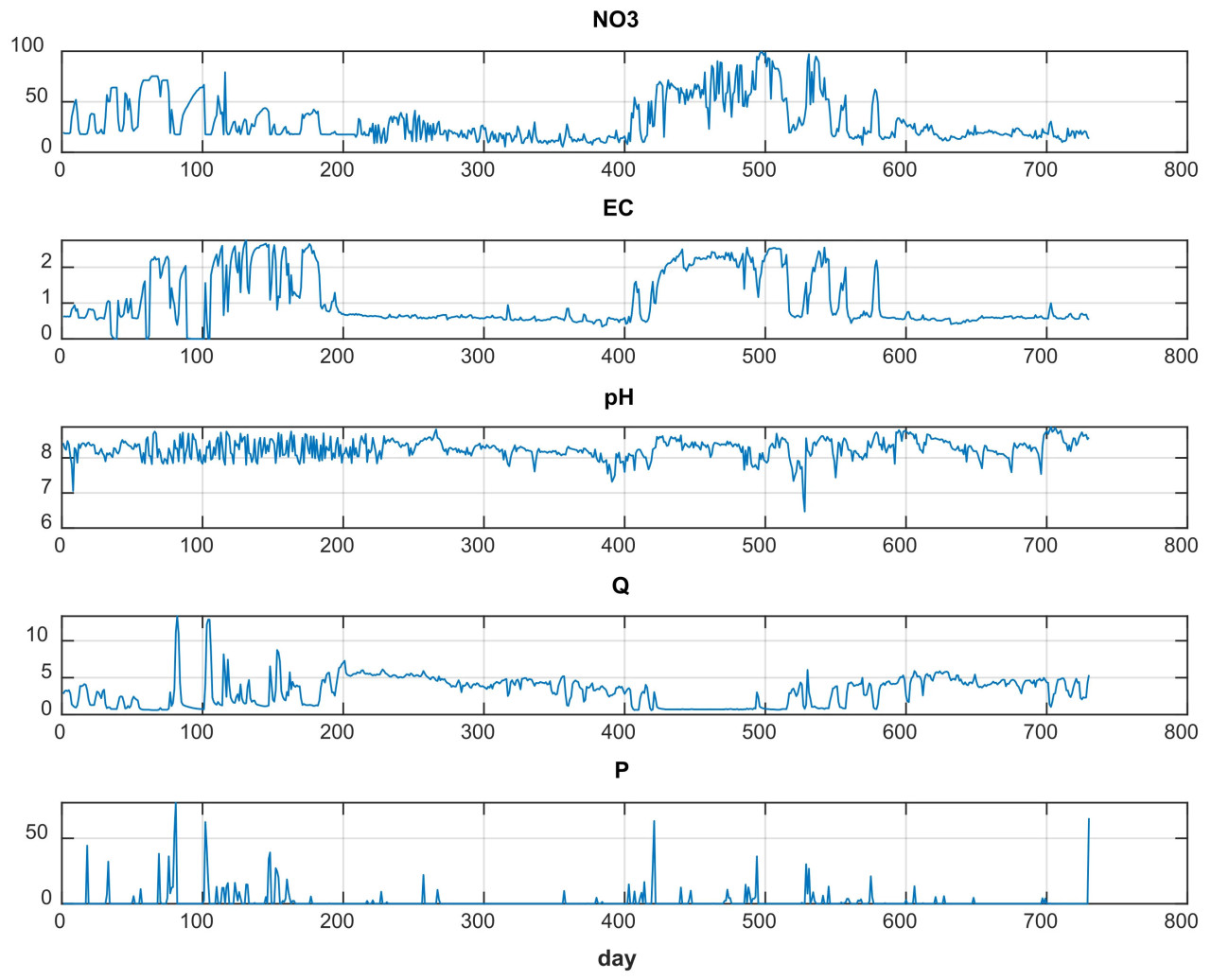
Временные вариации параметров, использованных в модели, и концентраций нитратов в течение 2022–2023 водных годов представлены на Рисунке 3. Как наблюдается на Рисунке 3, существует явная положительная корреляция между значениями нитратов и ЕС и обратная корреляция с Q. В целом можно заявить, что функциональной взаимосвязи между нитратами и другими параметрами нет. Однако примечательно, что эти параметры значительно влияют на производительность модели, особенно при прогнозировании экстремальных значений.

Рисунок 3. Временная вариация концентраций нитратов и входных данных модели.

2.3. Разработка модели ИНС для концентраций нитратов

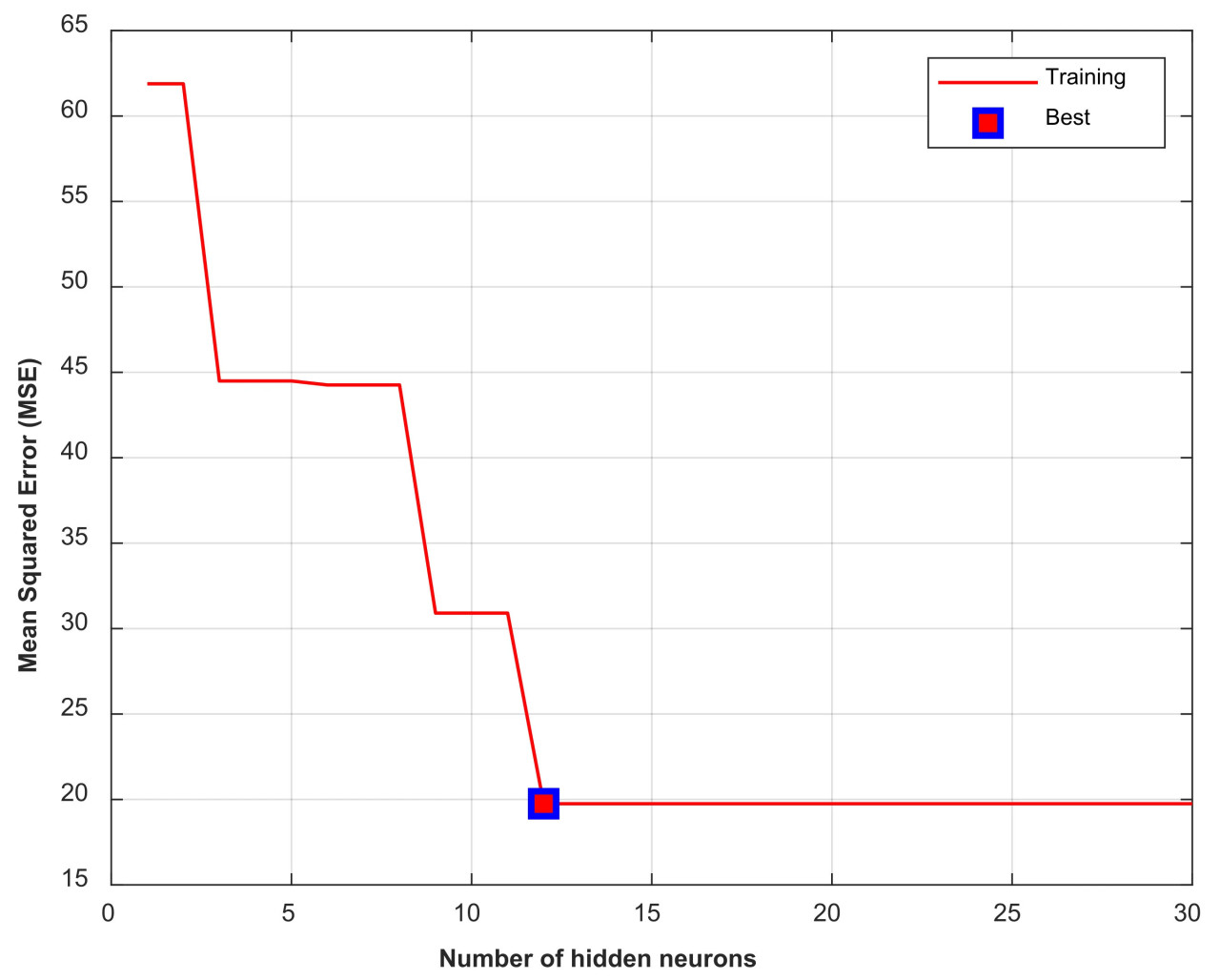
Для определения оптимального количества нейронов в скрытом слое 80% данных использовалось для обучения сети, а 20% — для тестирования. Этот процесс повторялся для 100 различных случайно выбранных наборов обучающих и тестовых данных, и рассчитывалось значение средней квадратической ошибки (MSE). Этот процесс повторялся в цикле от 1 до максимального количества нейронов, которое в данном исследовании составило 30; количество нейронов, которое давало минимальное значение MSE, выбиралось в качестве оптимального количества нейронов; и анализы проводились соответственно [61,62]. Как видно на Рисунке 4, оптимальное количество нейронов, полученное для Сценариев I и II, составило 12.

Рисунок 4. Трехслойная ИНС прямого распространения.

В процессе определения оптимального количества нейронов в скрытом слое и на протяжении всего процесса моделирования использовался алгоритм Левенберга-Марквардта — быстрый и эффективный алгоритм обучения, который сочетает точность метода Ньютона со стабильностью алгоритма градиентного спуска [63,64,65]. Гиперболический тангенс в качестве сигмоидной функции и линейная функция активации использовались в качестве функций активации в скрытом слое и выходном слое соответственно. Гиперболический тангенс в качестве сигмоидной функции, работающий в диапазоне от -1 до +1, обеспечивает более быструю способность к обучению в процессе обновления весов [66,67]. Между тем, линейная функция активации дает более естественные результаты в выходном слое, поскольку передает входные данные без какого-либо линейного искажения [68,69]. Предварительные испытания проводились для тестирования производительности алгоритма обучения и функций активации, и выборы были сделаны соответствующим образом. Анализы, выполненные на упомянутом компьютере, были завершены в течение времени обработки от 5 до 15 минут для каждого случая в зависимости от объема данных, использованных при обучении. Разработка, обучение и тестирование предложенной модели ИНС проводились на настольной рабочей станции с использованием языка программирования Python 3.13. Критерии производительности, использованные для определения производительности модели, приведены в Приложении A.

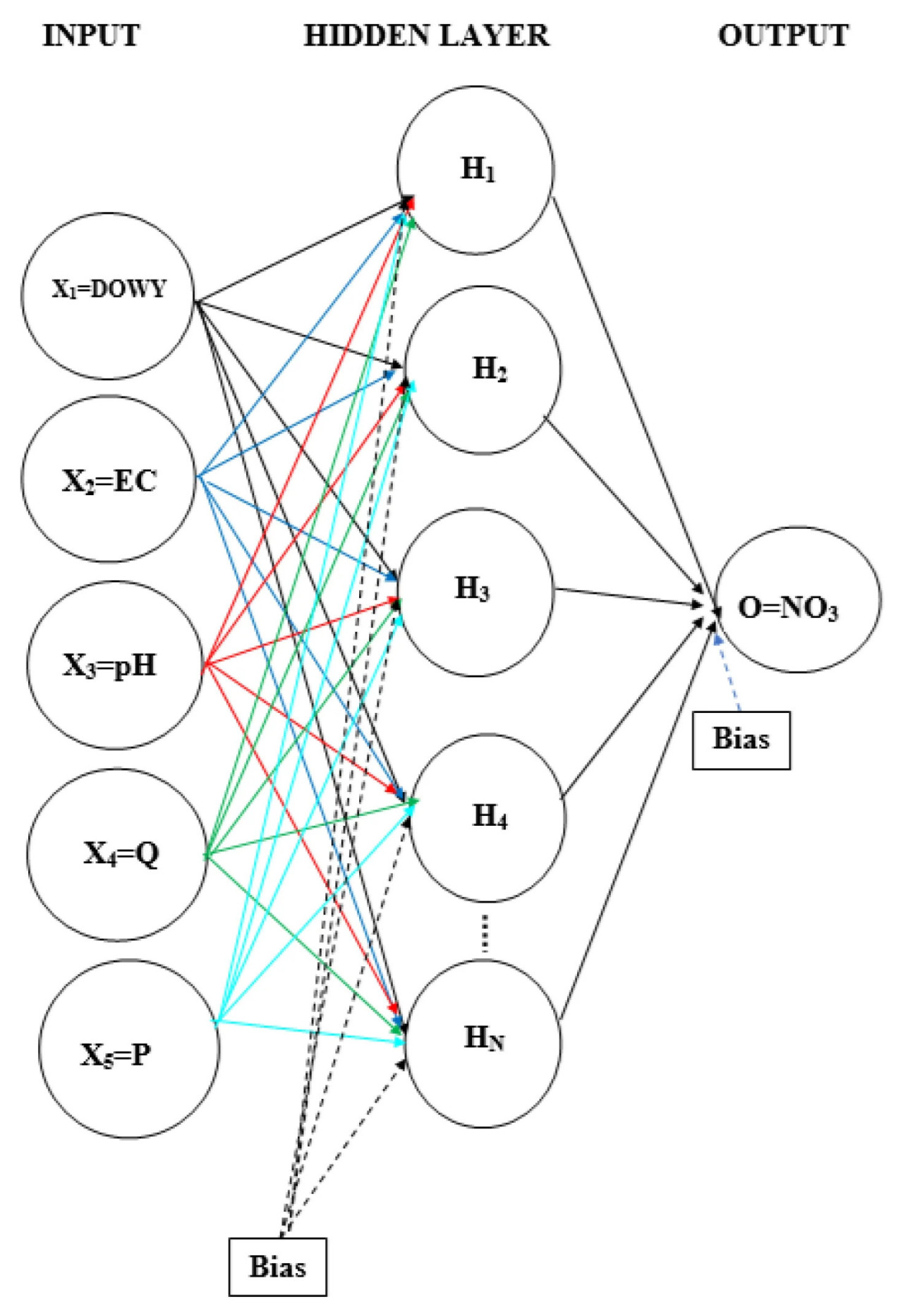
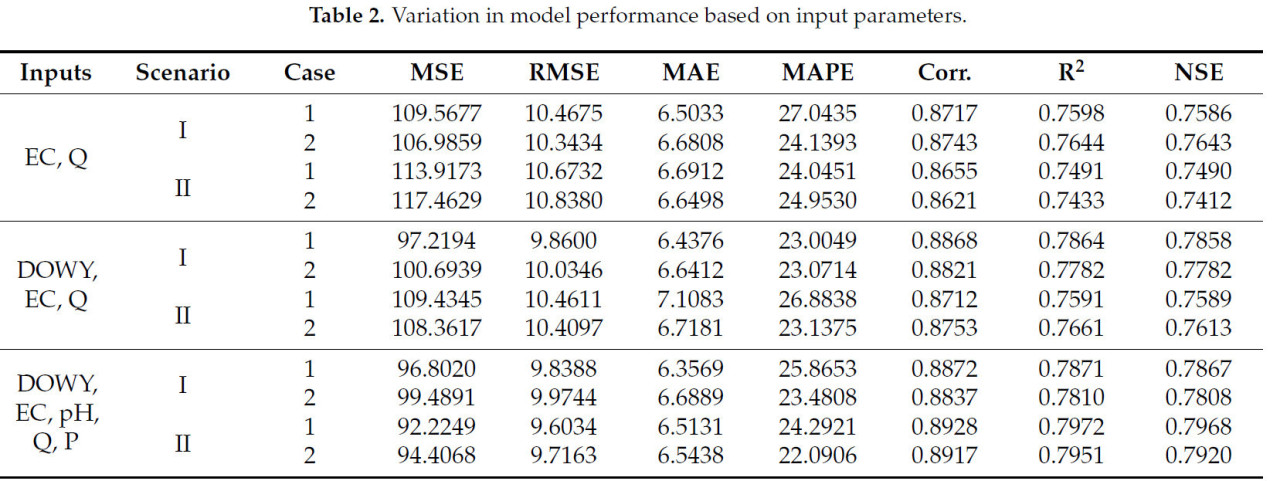
При выборе входных значений для модели учитывалась матрица корреляций. Изначально значения ЕС и Q, которые показали высокую корреляцию с нитратами, тестировались индивидуально. Впоследствии параметр DOWY был добавлен для демонстрации влияния времени. Наконец, значения pH и P, которые имеют низкую корреляцию с нитратами, были включены. Производительность модели для каждого из этих трех сценариев суммирована в Таблице 2 с использованием различных метрик оценки. Как показано в Таблице 2, два, три и пять параметров использовались в качестве входных данных соответственно. Они были выбраны как [EC, Q], [DOWY, EC, Q] и [DOWY, EC, pH, Q, P]. Среднеквадратическая ошибка (MSE), широко используемая метрика оценки ошибок в литературе, использовалась в качестве целевой функции для определения производительности модели. Дополнительно, полученные результаты оценивались с использованием других метрик оценки ошибок (RMSE, MAE, MAPE, коэффициент корреляции Пирсона, R², NSE), и производительность модели была суммирована в Таблице 2. Было отмечено сильное соответствие между результатами в Таблице 2 и матрицей корреляций. Даже когда параметры с высокой корреляцией с нитратами использовались в качестве входных данных, достигалась очень хорошая производительность. Однако, когда параметры с более низкой корреляцией включались в качестве входных данных, наблюдалось небольшое улучшение тестовой производительности модели. Это улучшение, примерно на 3–5%, более заметно на диаграммах рассеяния. Поэтому все упомянутые выше параметры использовались на этапах обучения и тестирования. После определения оптимального количества нейронов в скрытом слое как 12, оптимальная сетевая архитектура, используемая в модели, была определена как 5, 12 и 1 для входного, скрытого и выходного слоев соответственно, как показано на Рисунке 5.

Рисунок 5. Типичная структура многослойных ИНС, используемых в этом исследовании.

Таблица 2. Вариация производительности модели на основе входных параметров.

Модель ANN-Nitrate была реализована для 2022 и 2023 водных годов с использованием данных, полученных из района исследования, в двух сценариях. В Сценарии I данные, использованные на этапах обучения и тестирования, выбирались случайным образом из набора данных, в то время как в Сценарии II они выбирались в двух последовательных временных периодах. В Сценарии I цель состояла в прогнозировании значений нитратов для дней без измерений по разным причинам в пределах периода измерений, тогда как в Сценарии II цель состояла в прогнозировании значений до или после периода измерений. Для каждого сценария объемы данных, использованные на этапе обучения модели, выбирались как 20% и 50% от общего объема данных, обозначенных как случаи 1 и 2 соответственно.

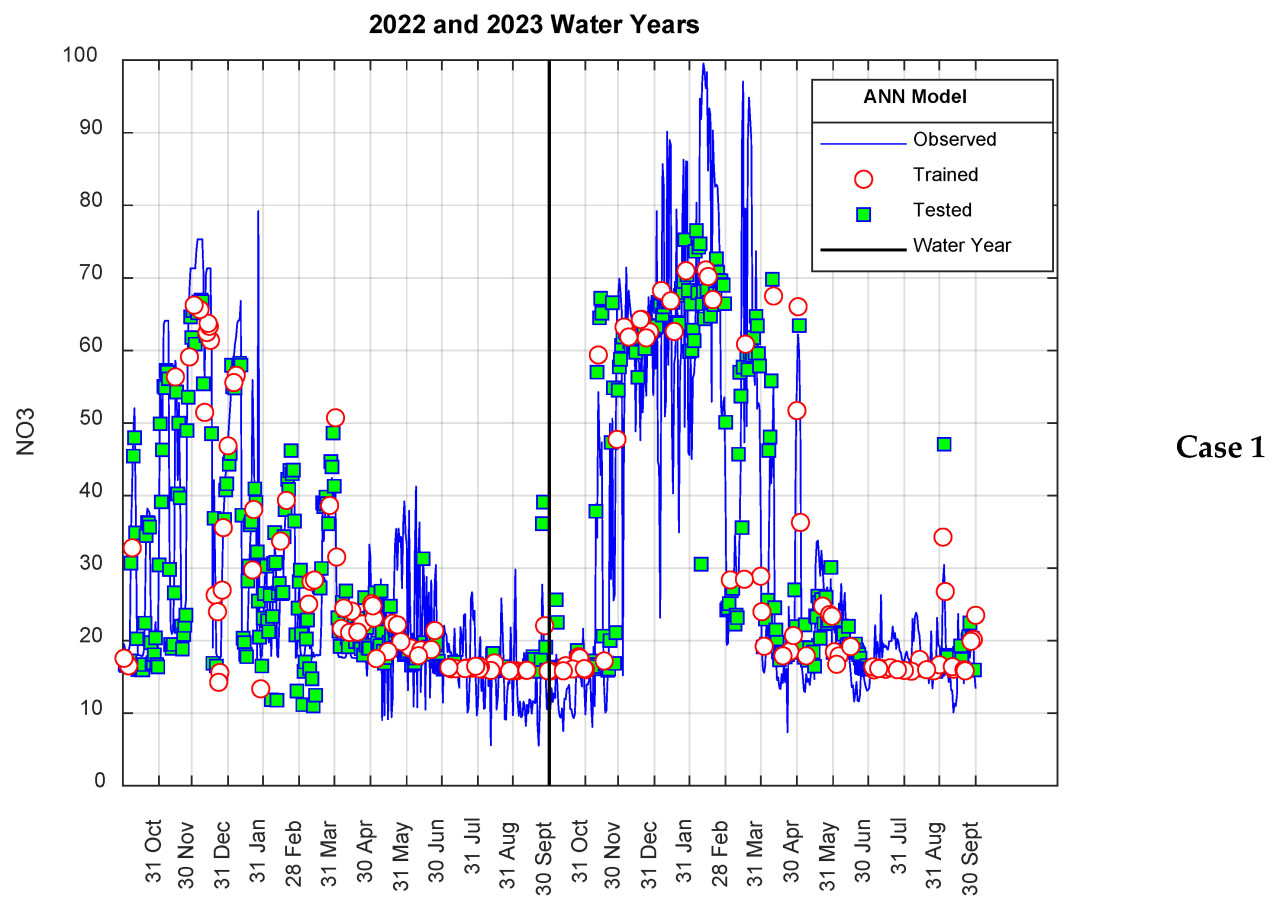
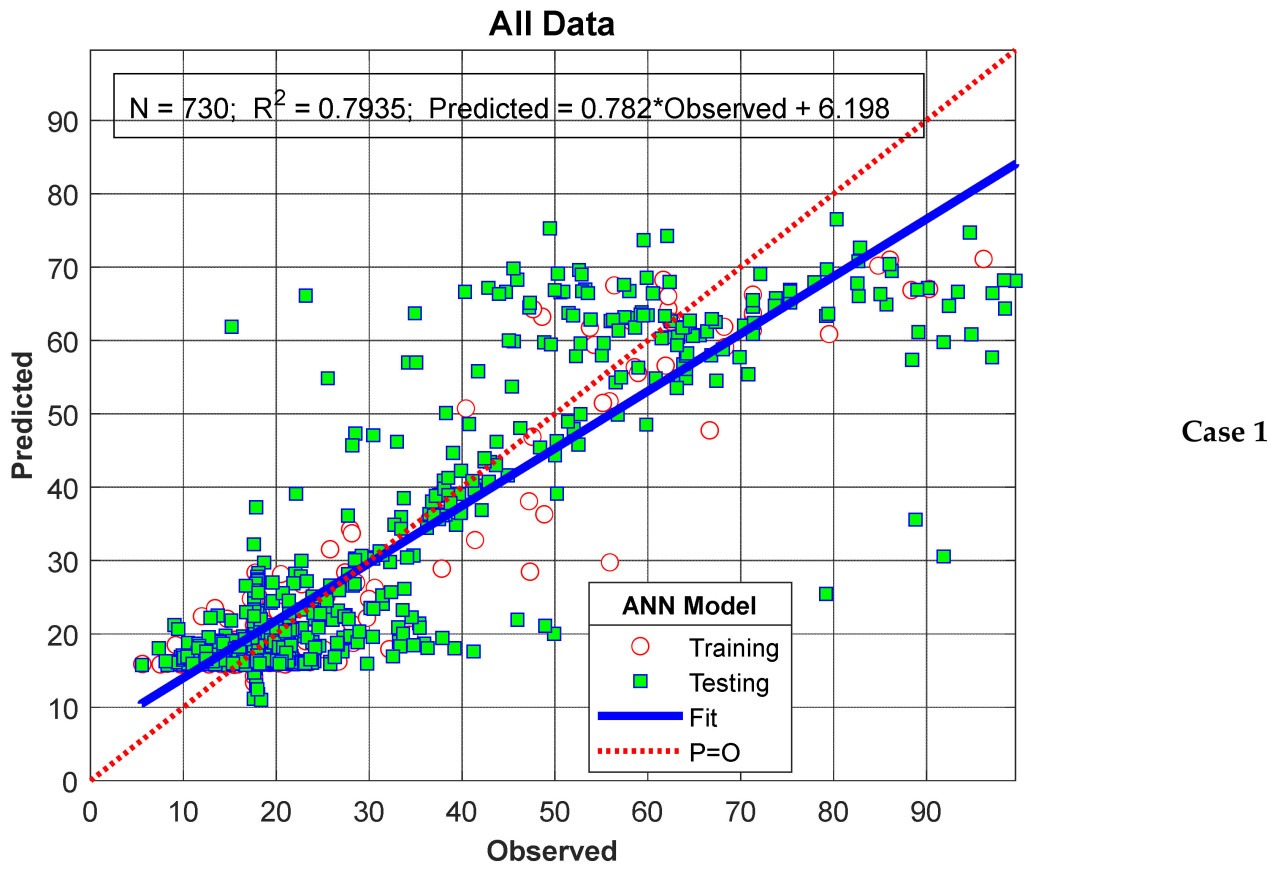
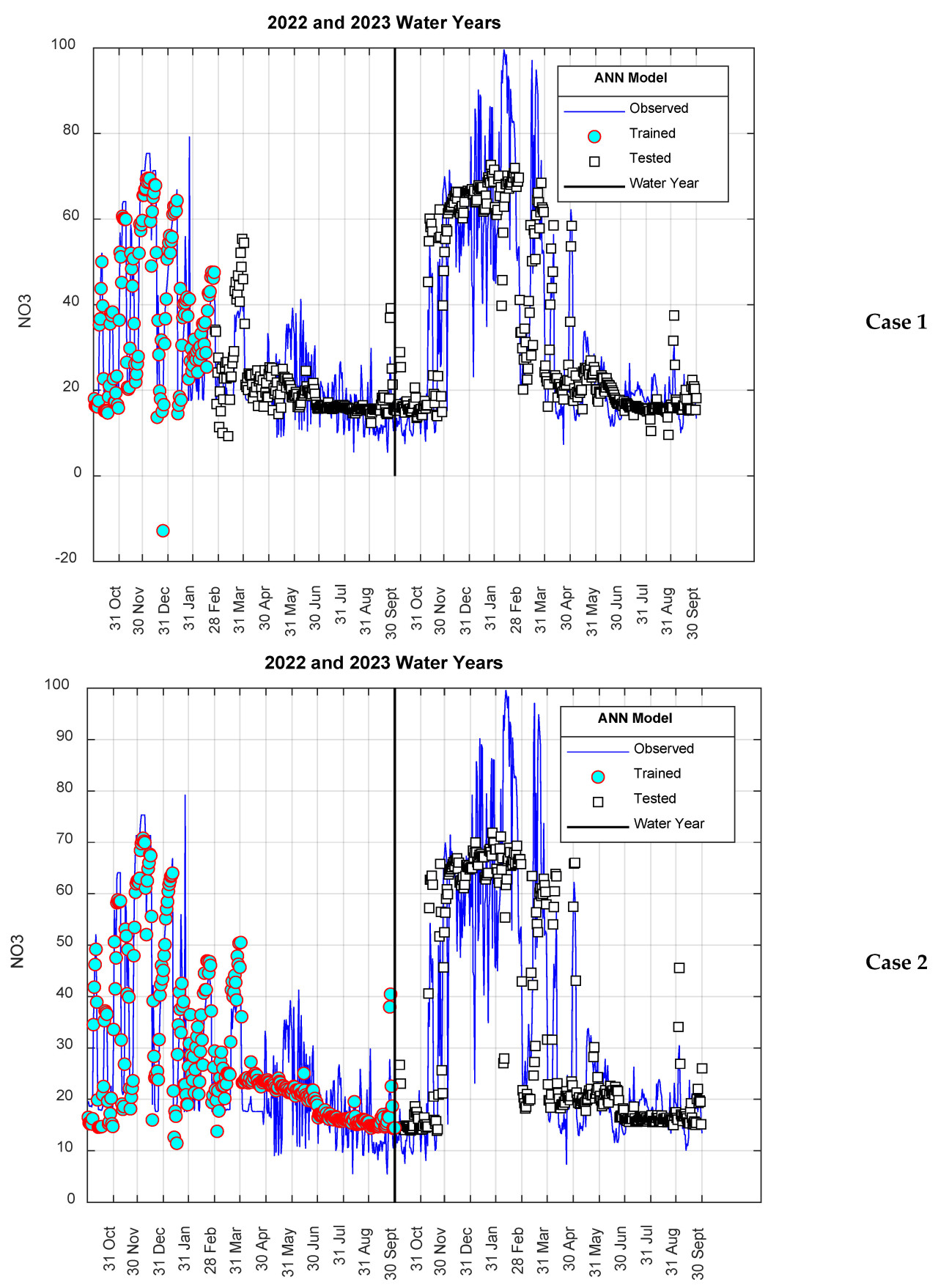
Измеренные значения и результаты модели для Сценария I представлены на Рисунке 6 как Случай 1 и Случай 2 соответственно. Как видно из Рисунка 6, результаты модели показывают хорошее согласие с измеренными значениями в обоих случаях и довольно хорошо представляют общую тенденцию. На Рисунке 7 согласованность результатов модели с измеренными значениями показана через диаграммы рассеяния. Значения R², рассчитанные для Случая 1 и Случая 2, составляют 0,7935 и 0,7831 соответственно, что считается указывающим на то, что предложенная модель обладает очень хорошей обобщающей и прогностической способностью.

Рисунок 6. Результаты модели для Сценария I.

Рисунок 7. Результаты модели для Сценария I.

Учитывая, что соотношение данных, обычно используемое в литературе на этапе обучения моделей ИНС [38,61,70], составляет между 0,70 и 0,80, тот факт, что результаты, полученные с использованием 20% набора данных, очень близки к результатам, полученным с использованием 50% набора данных, и что они довольно хорошо представляют фактическую ситуацию, указывает на то, что входные значения и архитектура модели могут быть хорошей альтернативой для прогнозирования значений нитратов.

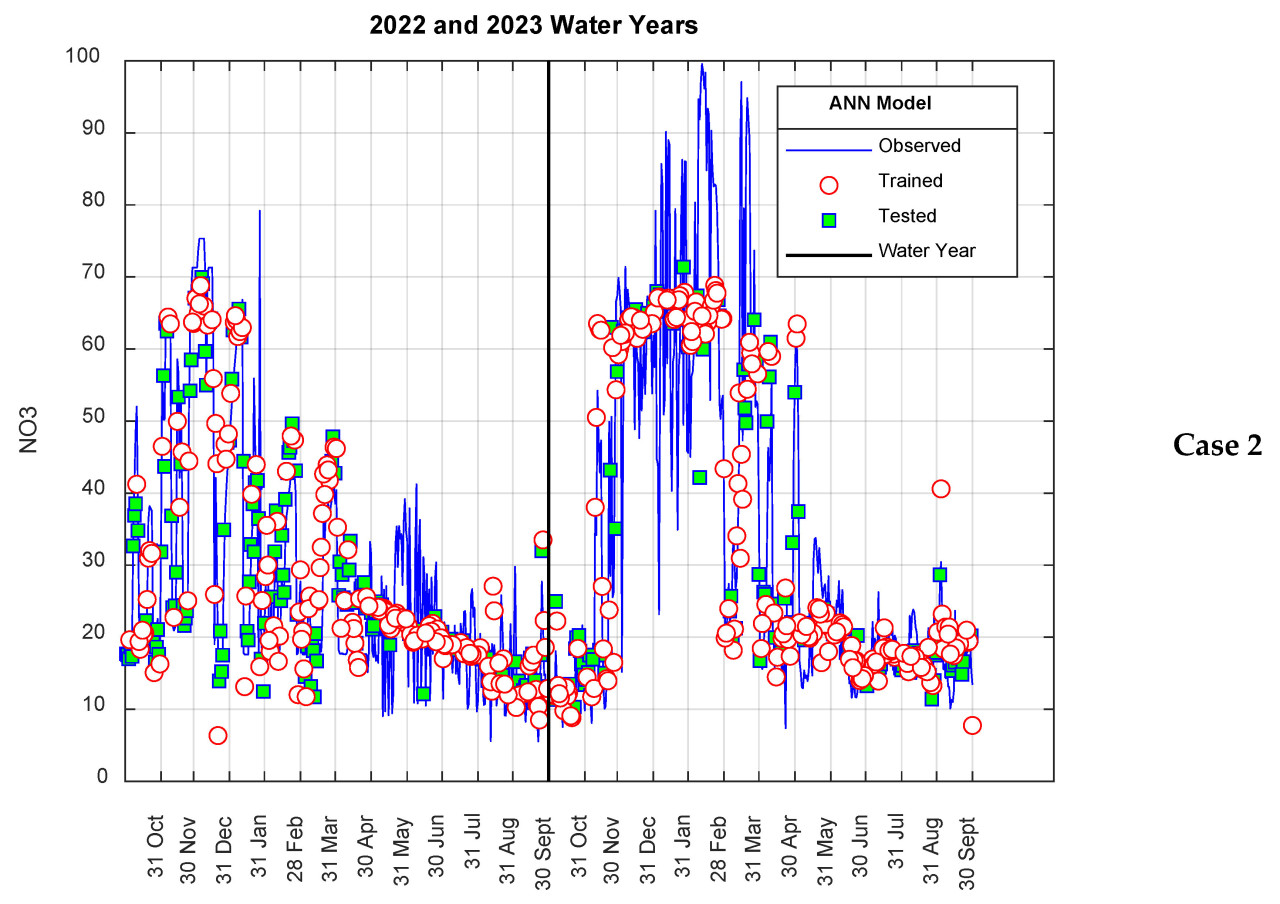
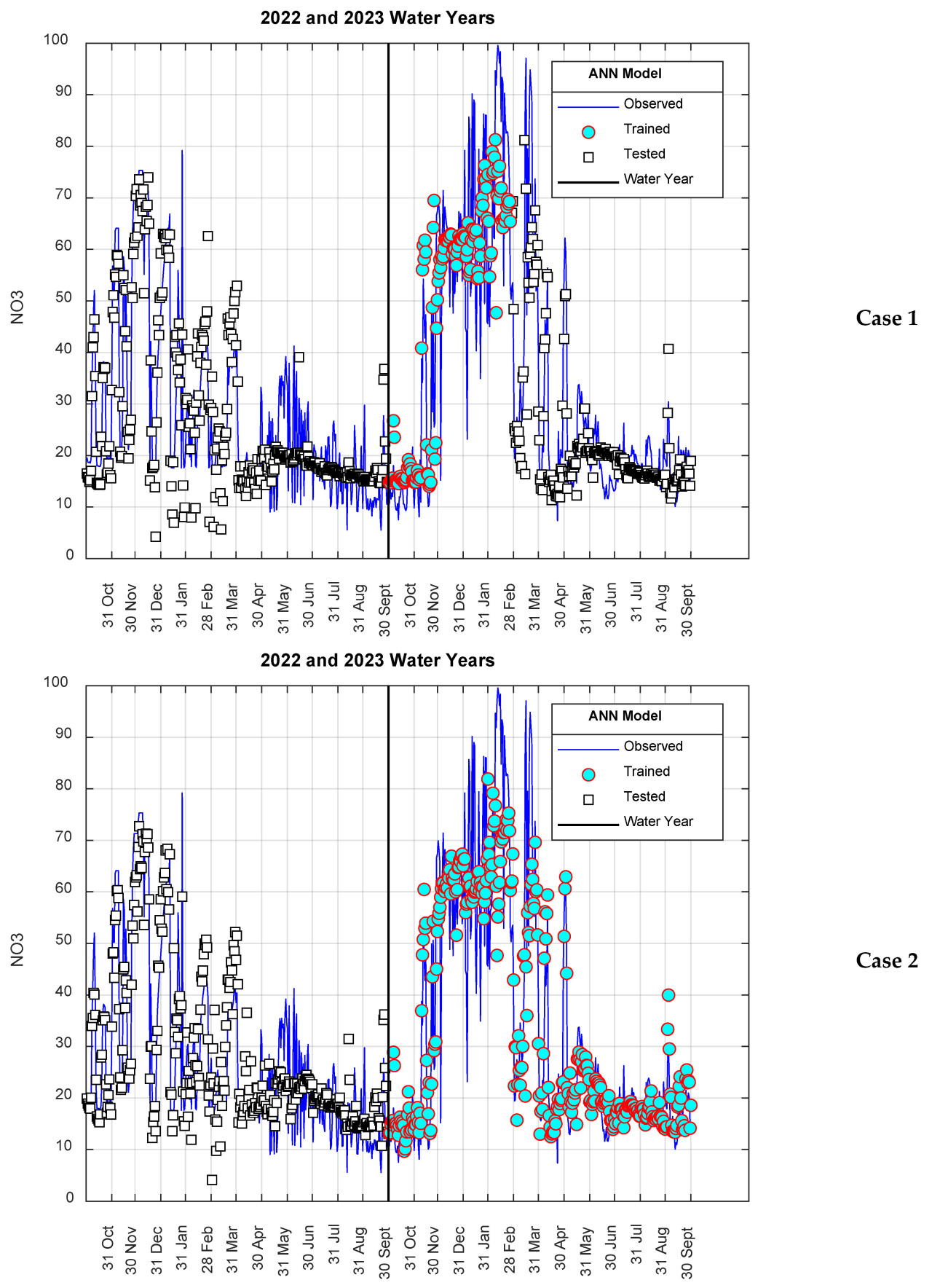
В Сценарии II, в отличие от Сценария I, данные, использованные для обучения и тестирования модели ANN-Nitrate, выбирались последовательно. На этапе обучения модели первые 0,20 и 0,50 части набора данных использовались для случая I и случая II соответственно, а оставшиеся 0,80 и 0,50 прогнозировались на этапе тестирования. Результаты, полученные для Сценария II, представлены на Рисунке 8. Как видно из Рисунка 8, было очень хорошее согласие между результатами модели и измеренными значениями нитратов, и общая тенденция была точно отражена.

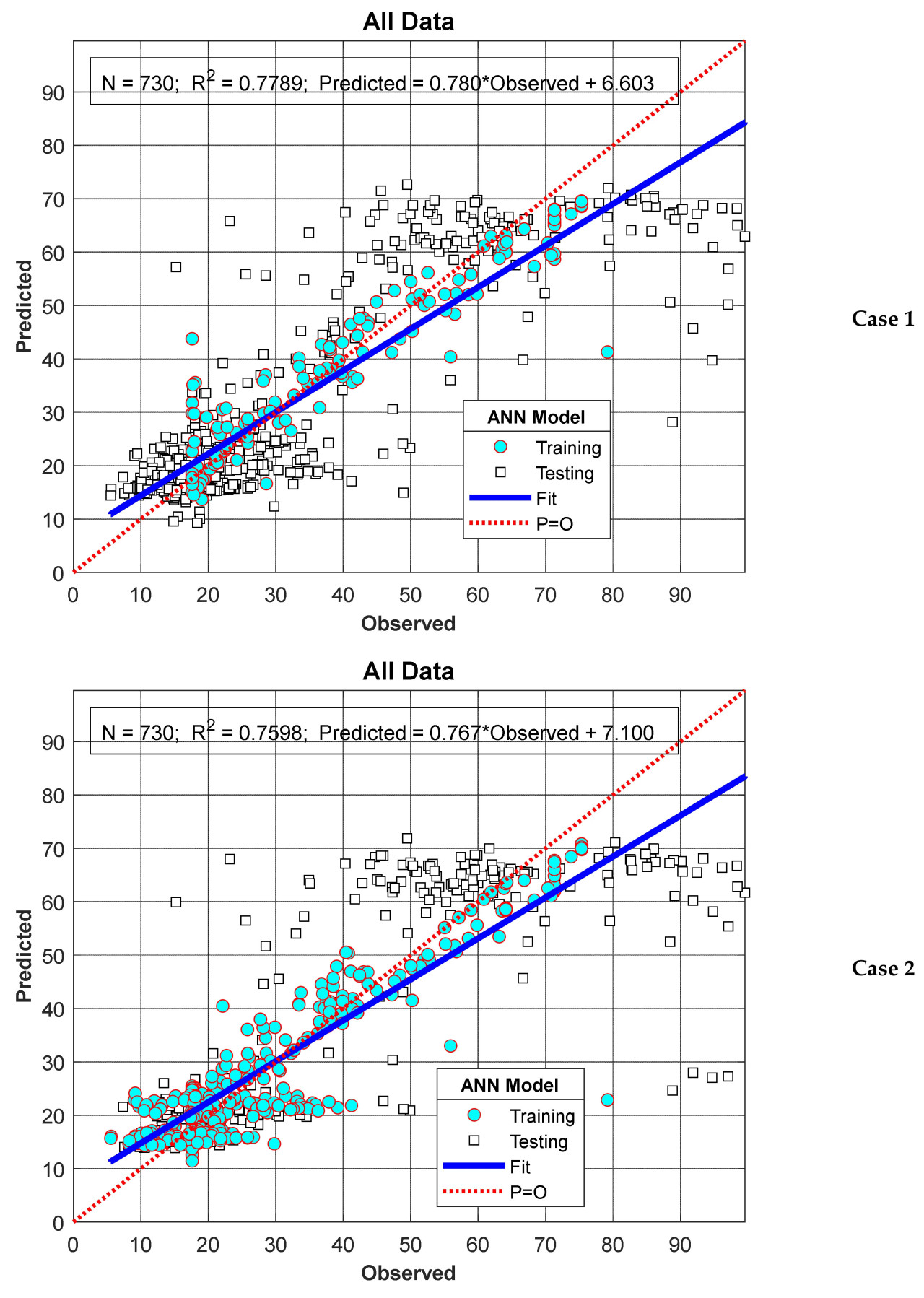
Рисунок 8. Результаты модели для Сценарии II.

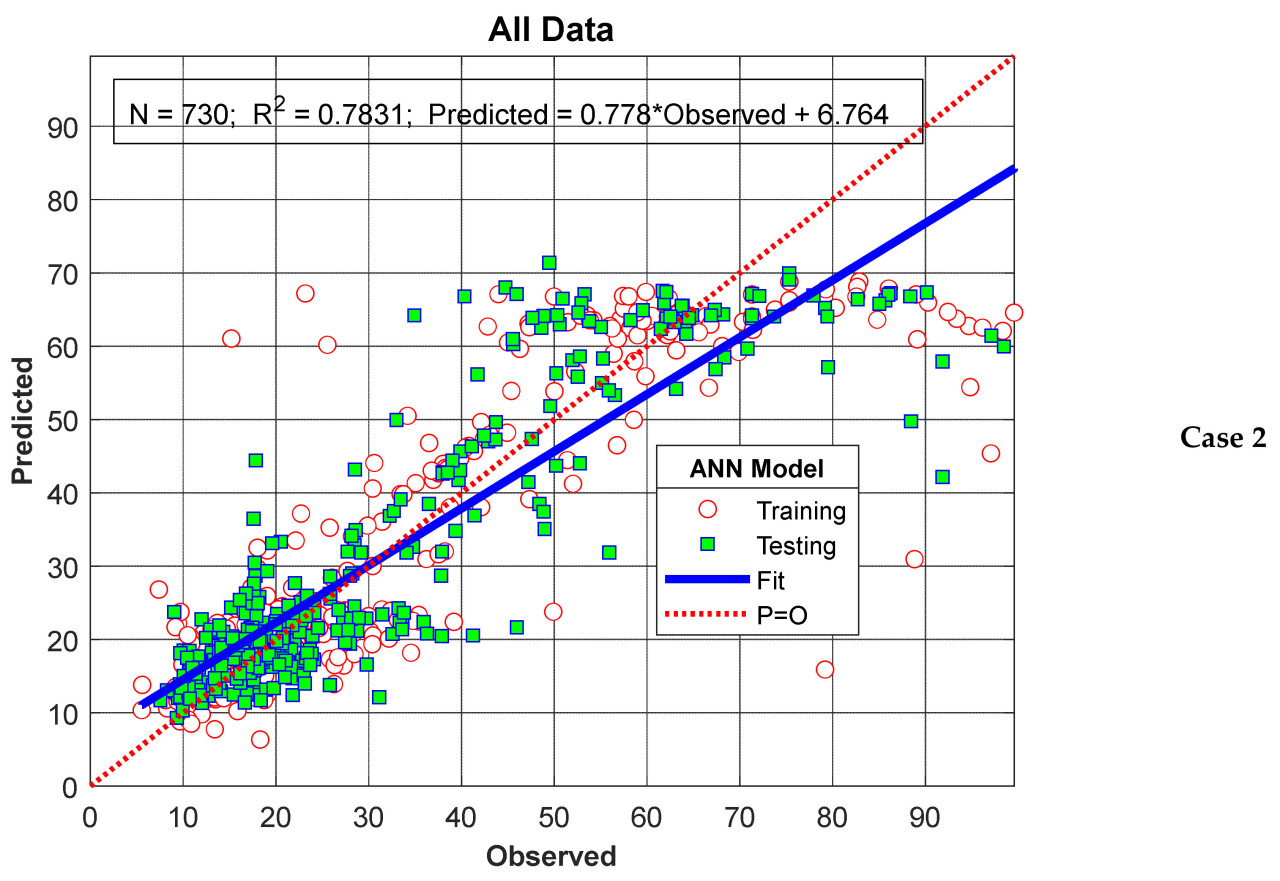
На Рисунке 9 результаты модели, полученные для Сценария II, представлены в виде диаграммы рассеяния против измеренных значений нитратов. Как показано на Рисунке 9, значения R² были рассчитаны как 0,7789 и 0,7598 для случая I и случая II соответственно. Можно отметить, что значения R², рассчитанные для Сценария II, несколько ниже, чем в Сценарии I. Однако, как видно в случае II, ожидается, что производительность модели будет снижаться по мере увеличения периода прогнозирования. Эта ситуация будет обсуждаться более подробно в следующем разделе.

Рисунок 9. Производительность модели для Сценария II.

4.1. Оптимальный выбор сети и факторы производительности в моделях ИНС

Выбор оптимальной сетевой структуры играет ключевую роль в производительности моделей ИНС, наряду с выбором алгоритмов обучения, функций активации, а также соотношением и методологией отбора обучающих данных. Оценки и комментарии по этой теме приведены ниже. В исследованиях моделей нитратов на основе ИНС значения корреляции Пирсона обычно используются для выбора входных данных [34,36,42,45,53]. Некоторые исследования также учитывают основные статистические параметры наряду со значениями корреляции Пирсона; однако анализы, основанные на значениях корреляции Пирсона, показали лучшую производительность [34]. В этом исследовании значения корреляции Пирсона учитывались при выборе входных данных. В отличие от других исследований, влияние входных данных на производительность модели определялось с помощью анализа, и результаты представлены подробно на основе различных критериев оценки ошибок. Было отмечено, что параметры с низкими коэффициентами корреляции Пирсона имели ограниченное влияние на результаты, хотя эти входные данные улучшали диаграммы рассеяния в моделях с низкими коэффициентами корреляции Пирсона.

Не существует стандартной формулы для определения оптимального количества нейронов. Однако в системах с ограниченными данными выбор большого количества скрытых нейронов улучшает производительность обучения, но снижает тестовую производительность модели [38,61,62,70]. Чтобы предотвратить переобучение, обычно используются вычислительно интенсивные методы, такие как поиск по сетке, случайный поиск или перекрестная проверка. Методы проб и ошибок обычно используются в исследованиях по моделированию нитратов [42,44,54]. Что касается алгоритмов обучения и функций активации, информация, как правило, недостаточна. В качестве критериев оценки ошибок различные метрики, такие как MSE, MAE и R², используются индивидуально или в комбинации.

В этом исследовании вместо использования вычислительно интенсивного метода проб и ошибок для оптимального выбора сети 80% данных использовалось для обучения и 20% для тестирования. Этот процесс повторялся для 100 случайно выбранных наборов обучающих и тестовых данных, и вычислялась средняя квадратическая ошибка (MSE). Эта процедура выполнялась в цикле до максимум 30 нейронов. Количество нейронов, которое обеспечивало минимальную MSE, выбиралось в качестве оптимального, и анализы проводились соответственно [61,62,70].

Для определения оптимальной сетевой структуры обычно используемые в литературе алгоритмы обучения и функции активации варьировались случайным образом, одновременно определяя наиболее подходящий алгоритм обучения и функции активации для данных. В результате алгоритм Левенберга-Марквардта был определен как лучший алгоритм обучения, а гиперболический тангенс в качестве сигмоидной функции для скрытого слоя и линейная функция активации для выходного слоя были определены как лучшие функции активации. Таким образом, оптимальная архитектура сети, алгоритм обучения и функции активации были определены за один шаг. Эта процедура была применена впервые в этом исследовании и считается значительным вкладом в моделирование ИНС.

Данные, использованные в этом исследовании, были собраны со станции, которая собирает все дренажные воды реального орошаемого поля за два водных года (2022–2023) посредством ежедневных измерений и лабораторных анализов, что привело к 730 ежедневным наборам данных. В литературе данные, используемые в моделях нитратов, часто собираются из разных мест и времени. Дополнительно, длина данных сообщается как 316 в [45], а [42] и [36] следуют с 112 и 67 соответственно.

Поэтому, хотя производительность модели на основе критериев оценки ошибок высока, изменчивость в длине данных и использование данных из разных мест и времени считаются ограничивающими факторами для лиц, принимающих решения, и практиков. Для устойчивого сельского хозяйства и управления водными ресурсами необходимы непрерывные измерения и поддержка исследователей, поскольку получение таких данных особенно сложно в развивающихся странах. Следовательно, это исследование, основанное на ежедневных измерениях с одной станции с использованием реальных данных, считается значимым для лиц, принимающих решения, и практиков с точки зрения как методологии, так и практического применения.

4.2. Соотношения данных и методы отбора при обучении и тестировании

Другим важным фактором, влияющим на производительность моделей ИНС, является соотношение и метод отбора данных, используемых во время обучения и тестирования. Как правило, 80% от общего объема данных используется для обучения, а 20% — для тестирования [38,61,62,70]. Большинство публикаций по моделированию нитратов также используют эти соотношения со случайным отбором. В этом исследовании соотношение обучающих данных было увеличено с 10% до 80%, и производительность была проанализирована. Поскольку значительного улучшения не наблюдалось после 20%, в Сценарии 1 использовалось 20% от общего объема данных для обучения, а в Сценарии 2 — 50%. Оставшиеся данные использовались для тестирования. Хотя использование 20% от общего объема данных для обучения дало удовлетворительные результаты, в Сценарии 2 было выбрано 50% для оценки прогностической производительности одного года на основе обучающих данных другого года в двухлетнем наборе данных.

Каждый сценарий включает два случая: Случай 1 включал случайный отбор данных, в то время как Случай 2 включал последовательный отбор в виде временного ряда. В обоих сценариях производительность модели оценивалась как очень хорошая на основе значений NSE [43], причем случайный отбор показал немного лучшую производительность. Когда данные отбираются последовательно, необходимо позаботиться о включении экстремальных значений в обучающие данные. Подробные анализы по этому вопросу приведены ниже.

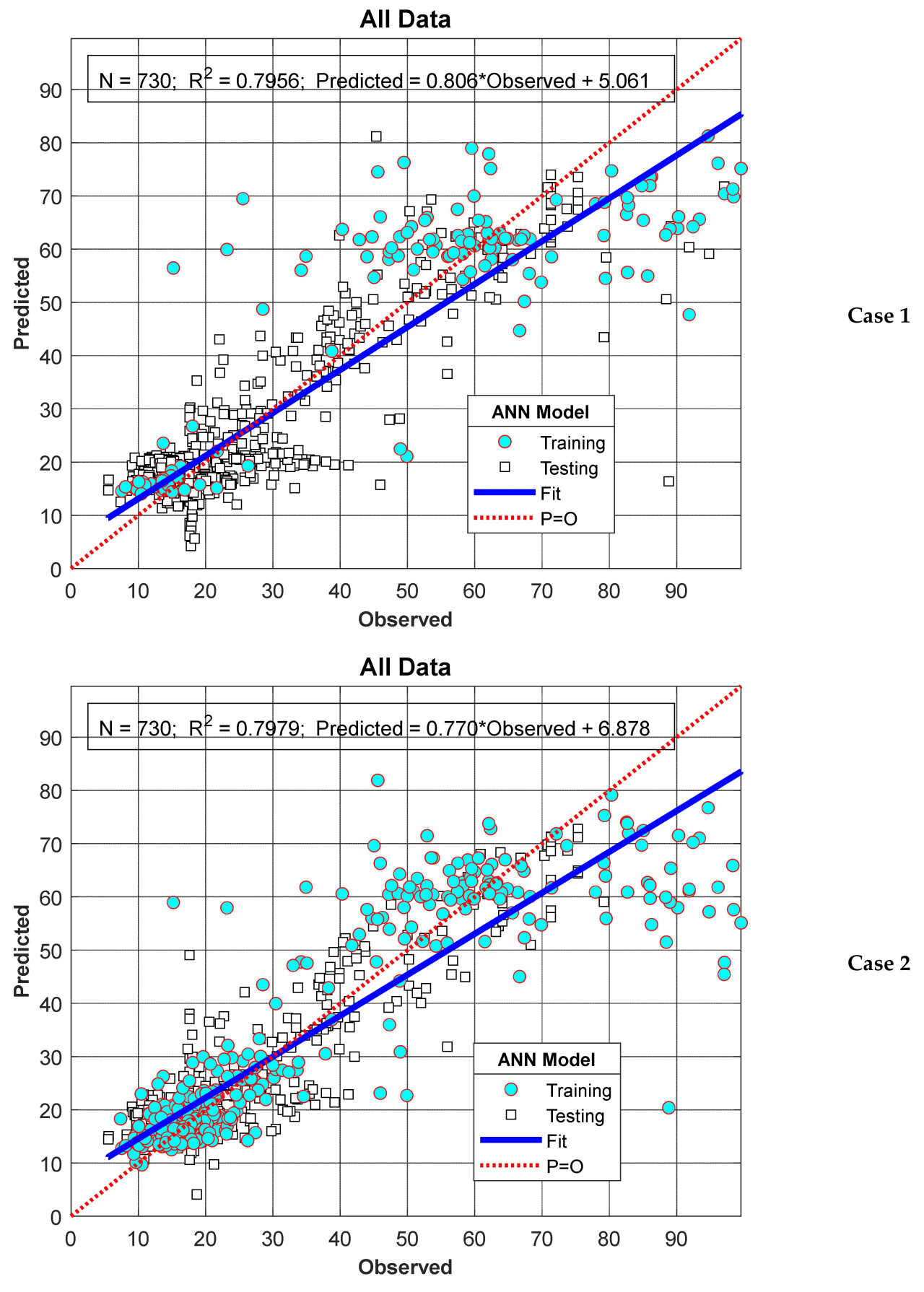
При оценке результатов модели ANN-Nitrate, представленных в предыдущем разделе, очевидно, что результаты, полученные для Сценария I, были лучше, чем для Сценария II. Считается, что это связано с тем, что в Сценарии I данные, использованные для этапов обучения и тестирования, выбирались случайным образом из всей серии, в то время как в Сценарии II данные выбирались как последовательный временной ряд. Как ясно видно из Рисунков 6 и 8, хотя значения нитратов, измеренные для 2022 водного года, показали аналогичную тенденцию с таковыми для 2023 года, они были относительно меньше. Поэтому, поскольку все данные, использованные на этапе обучения для Сценария II, относились к 2022 году, тестовая производительность была немного ниже по сравнению со Сценарием I. Эта ситуация особенно более заметна в Случае II. Это связано с тем, что все данные, использованные на этапе обучения Случая II, принадлежали 2022 году, в то время как результаты модели, рассчитанные на этапе тестирования, полностью принадлежали 2023 водному году. Чтобы проверить этот аргумент, в этом разделе данные за 2023 год вместо 2022 года были использованы в фазе обучения модели, и значения за 2022 год были рассчитаны как тестовые данные. Другими словами, обучающие и тестовые данные, использованные в Сценарии II, были поменяны местами, и анализ был повторен. Результаты суммированы на Рисунках 10 и 11. Как ясно видно из Рисунка 10, хотя пиковые значения за 2022 год были очень хорошо предсказаны, отклонения в минимальных значениях показали значительный рост. С другой стороны, как показано на Рисунке 11, значения R² увеличились до 0,7956 и 0,7979 для случаев I и II соответственно. Другими словами, наблюдалось заметное улучшение производительности модели.

Рисунок 10. Результаты модели для Сценария II.

Рисунок 11. Производительность модели для Сценария II.

Из моментов, поднятых в предыдущем разделе, и обсуждений в этом разделе ясно, что общая производительность Сценария I была лучше, чем Сценария II. Однако, учитывая, что цели двух сценариев были разными и что результаты Сценария II также были вполне удовлетворительными с практической точки зрения, можно сделать вывод, что предложенная модель может надежно использоваться для обоих сценариев.

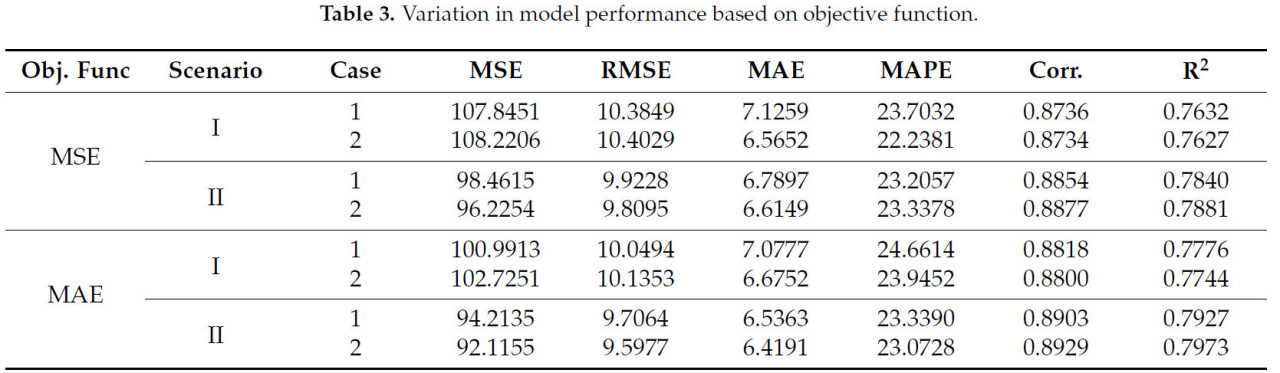
Анализы, проведенные в разделе 2, использовали R² и MSE в качестве целевых функций для определения оптимальной архитектуры сети для предложенной модели и для наблюдения влияния входных параметров на производительность модели. Однако производительность модели была пересчитана на основе всех метрик оценки ошибок с использованием полученных результатов и представлена для сравнения в Таблице 2. Как ясно показано в Таблице 2, производительность модели была высоко стабильной и практически удовлетворительной во всех сценариях и условиях на основе всех метрик оценки. Чтобы поддержать этот аргумент, все расчеты были повторены для обоих сценариев с использованием MSE и MAE в качестве целевых функций. Производительности моделей на основе всех метрик оценки суммированы в Таблице 3 с использованием полученных результатов. Как ясно видно из Таблицы 3, когда значения R² рассчитывались на основе результатов, полученных с использованием MAE и MSE в качестве целевых функций, было очень сильное соответствие со значениями R², предоставленными между Рисунками 6 и 11. Это демонстрирует, что производительность предложенной модели и архитектуры сети не изменялась в зависимости от используемой метрики оценки ошибок.

Таблица 3. Вариация производительности модели на основе целевой функции.

Это исследование было направлено на разработку модели на основе ИНС для определения концентраций нитратов в дренажных водах в пределах орошаемой зоны, расположенной в Нижнем бассейне реки Сейхан, одном из значимых сельскохозяйственных производственных регионов Турции. С этой целью пробы воды отбирались ежедневно в течение 2022 и 2023 водных лет на станции, где собираются дренажные воды со всей орошаемой зоны, и концентрации нитратов определялись в лаборатории. Наряду с концентрациями нитратов другие параметры, такие как расход, электропроводность, pH и осадки, также измерялись одновременно на той же станции. Сложная взаимосвязь между измеренными значениями нитратов и другими параметрами, которые легче и дешевле измерять, использовалась в двух различных сценариях на этапе обучения модели ANN-Nitrate. Модель, после обучения, предсказывала значения нитратов с использованием других параметров. В Сценарии I предсказывались случайные значения, в то время как в Сценарии II предсказания выполнялись в виде временного ряда, и результаты модели сравнивались с измеренными значениями.

Для Сценария I случай 1, производительности модели (R²) для обучения, тестирования и всего набора данных составили 0,8805, 0,7732 и 0,7935 соответственно, в то время как для случая 2 они составили 0,7637, 0,8048 и 0,7831 соответственно. Как наблюдалось, несмотря на то, что доли данных, использованные при обучении модели, варьировались от 0,20 до 0,50 от общего объема данных в обоих случаях, не было значительного изменения производительности модели для полного набора данных. Этот результат считается следствием тщательного выбора как параметров, использованных при обучении модели ANN-Nitrate, так и сетевой архитектуры модели. Дополнительно, обучение модели с меньшим количеством данных и достижение высокой тестовой производительности подчеркивает еще один значительный аспект этого исследования.

Аналогично, в Сценарии II случай 1, производительности модели (R²) для обучения, тестирования и всего набора данных составили 0,8722, 0,7498 и 0,7789 соответственно, в то время как для случая 2 они составили 0,8422, 0,7155 и 0,7598 соответственно. Общая производительность Сценария I казалась лучше, чем Сценария II. Однако, учитывая, что каждый сценарий служил разной цели и что Сценарий II также предоставлял практически удовлетворительные результаты, можно сказать, что предложенная модель может надежно использоваться для обоих сценариев.

Предложенная модель, основанная на искусственных нейронных сетях (ИНС), предназначена для прогнозирования концентраций нитратов в дренажных водах в пределах Нижнего бассейна реки Сейхан, одного из ключевых сельскохозяйственных регионов Турции, с использованием параметров, которые проще и экономически эффективнее измерять. Однако она также имеет потенциал для применения к другим методам, обычно используемым в машинном обучении и искусственном интеллекте, таким как машины опорных векторов (SVM), деревья решений, случайные леса, ансамблевые методы и методы глубокого обучения. Дополнительно, модель может использоваться без необходимости каких-либо модификаций для других бассейнов, где измеряются входные значения. Будущие исследования планируются для применения модели к другим бассейнам для повышения ее обобщаемости и для сравнения тестовых производительностей упомянутых методов систематическим образом.

В заключение, способность точно прогнозировать нитраты — значимый параметр с точки зрения орошения и общего качества воды — с использованием модели на основе ИНС с параметрами, которые легче и дешевле измерять, такими как ЕС, pH, Q и P, считается важным вкладом этого исследования в литературу. Эта модель помогает как в заполнении отсутствующих данных, так и в прогнозировании на будущее.

1.    McNeely, R.N.; Neimanis, V.P.; Dwyer, L. Water Quality Sourcebook: A Guide to Water Quality Parameters; Inland Waters Directorate, Water Quality Branch: Ottawa, Canada, 1979; pp. 1–89. [Google Scholar]

2.    Hem, J.D. Study and Interpretation of the Chemical Characteristics of Natural Water; Department of the Interior, US Geological Survey: Alexandria, VA, USA, 1985; Volume 2254. [Google Scholar]

3.    Benzer, S.; Benzer, R. Modelling nitrate prediction of groundwater and surface water using artificial neural networks. J. Polytech. 2018, 21, 321–325. [Google Scholar] [CrossRef]

4.    Sharma, V.; Negi, S.C.; Rudra, R.P.; Yang, S. Neural networks for predicting nitrate-nitrogen in drainage water. Agric. Water Manag. 2003, 63, 169–183. [Google Scholar] [CrossRef]

5.    Horsburgh, J.S.; Hooper, R.P.; Bales, J.; Hedstrom, M.; Imker, H.J.; Lehnert, K.A.; Shanley, L.A.; Stall, S. Assessing the state of research data publication in hydrology: A perspective from the Consortium of Universities for the Advancement of Hydrologic Science, Incorporated. Wiley Interdiscip. Rev. Water 2020, 7, e1422. [Google Scholar] [CrossRef]

6.    McDonough, L.K.; Santos, I.R.; Andersen, M.S.; O’Carroll, D.M.; Rutlidge, H.; Meredith, K.; Oudone, P.; Bridgeman, J.; Goddy, D.C.; Sorensen, J.P.; et al. Changes in global groundwater organic carbon driven by climate change and urbanization. Nat. Commun. 2020, 11, 1279. [Google Scholar] [CrossRef]

7.    Misstear, B.; Vargas, C.R.; Lapworth, D.; Ouedraogo, I.; Podgorski, J. A global perspective on assessing groundwater quality. Hydrogeol. J. 2023, 31, 11–14. [Google Scholar] [CrossRef]

8.    Basu, N.B.; Van Meter, K.J.; Byrnes, D.K.; Van Cappellen, P.; Brouwer, R.; Jacobsen, B.H.; Jarsjö, J.; Rudolph, D.L.; Cunha, M.C.; Nelson, N.; et al. Managing nitrogen legacies to accelerate water quality improvement. Nat. Geosci. 2022, 15, 97–105. [Google Scholar] [CrossRef]

9.    Foster, S.S.D.; Chilton, P.J. Groundwater: The processes and global significance of aquifer degradation. Philosophical Transactions of the Royal Society of London. Ser. B Biol. Sci. 2003, 358, 1957–1972. [Google Scholar] [CrossRef]

10. Jasechko, S.; Perrone, D. Global groundwater wells at risk of running dry. Science 2021, 372, 418–421. [Google Scholar] [CrossRef]

11. Torres-Martínez, J.A.; Mahlknecht, J.; Kumar, M.; Loge, F.J.; Kaown, D. Advancing groundwater quality predictions: Machine learning challenges and solutions. Sci. Total Environ. 2024, 949, 174973. [Google Scholar] [CrossRef]

12. Palani, S.; Liong, S.Y.; Tkalich, P. An ANN application for water quality forecasting. Mar. Pollut. Bull. 2008, 56, 1586–1597. [Google Scholar] [CrossRef]

13. Zare, A.; Bayat, V.; Daneshkare, A. Forecasting nitrate concentration in groundwater using artificial neural network and linear regression models. Int. Agrophysics 2011, 25, 2–187. [Google Scholar]

14. Mahlknecht, J.; Torres-Martínez, J.A.; Kumar, M.; Mora, A.; Kaown, D.; Loge, F.J. Nitrate prediction in groundwater of data scarce regions: The futuristic fresh-water management outlook. Sci. Total Environ. 2023, 905, 166863. [Google Scholar] [CrossRef] [PubMed]

15. Podgorski, J.; Berg, M. Global analysis and prediction of fluoride in groundwater. Nat. Commun. 2022, 13, 4232. [Google Scholar] [CrossRef] [PubMed]

16. Podgorski, J.; Berg, M. Global threat of arsenic in groundwater. Science 2020, 368, 845–850. [Google Scholar] [CrossRef] [PubMed]

17. Sarkar, S.; Mukherjee, A.; Chakraborty, M.; Quamar, M.T.; Duttagupta, S.; Bhattacharya, A. Prediction of elevated groundwater fluoride across India using multi-model approach: Insights on the influence of geologic and environmental factors. Environ. Sci. Pollut. Res. 2023, 30, 31998–32013. [Google Scholar] [CrossRef]

18. Alengebawy, A.; Abdelkhalek, S.T.; Qureshi, S.R.; Wang, M.Q. Heavy metals and pesticides toxicity in agricultural soil and plants: Ecological risks and human health implications. Toxics 2021, 9, 42. [Google Scholar] [CrossRef]

19. Hube, S.; Wu, B. Mitigation of emerging pollutants and pathogens in decentralized wastewater treatment processes: A review. Sci. Total Environ. 2021, 779, 146545. [Google Scholar] [CrossRef]

20. Yaseen, Z.M.; Ebtehaj, I.; Bonakdari, H.; Deo, R.C.; Mehr, A.D.; Mohtar, W.H.M.W.; Diop, L.; El-shafie, A.; Singh, V.P. Novel approach for streamflow forecasting using a hybrid ANFIS-FFA model. J. Hydrol. 2017, 554, 263–276. [Google Scholar] [CrossRef]

21. Sarangi, A.; Singh, M.; Bhattacharya, A.K.; Singh, A.K. Subsurface drainage performance study using SALTMOD and ANN models. Agric. Water Manag. 2006, 84, 240–248. [Google Scholar] [CrossRef]

22. Karahan, H.; Ayvaz, M.T. Forecasting aquifer parameters using artificial neural networks. J. Porous Media 2006, 9, 429–444. [Google Scholar] [CrossRef]

23. Logan, T.J.; Eckert, D.J.; Beak, D.G. Tillage, crop and climatic effects of runoff and tile drainage losses of nitrate and four herbicides. Soil Tillage Res. 1994, 30, 75–103. [Google Scholar] [CrossRef]

24. Strik, D.P.; Domnanovich, A.M.; Zani, L.; Braun, R.; Holubar, P. Prediction of trace compounds in biogas from anaerobic digestion using the MATLAB Neural Network Toolbox. Environ. Modell. Softw. 2005, 20, 803–810. [Google Scholar] [CrossRef]

25. Koekkoek, E.J.W.; Booltink, H. Neural network models to predict soil water retention. Eur. J. Soil Sci. 1999, 50, 489–495. [Google Scholar] [CrossRef]

26. Co, H.C.; Boosarawongse, R. Forecasting Thailand’s rice export: Statistical techniques vs. artificial neural networks. Comput. Ind. Eng. 2007, 53, 610–627. [Google Scholar] [CrossRef]

27. Erzin, Y.; Rao, B.H.; Singh, D.N. Artificial neural network models for predicting soil thermal resistivity. Int. J. Therm. Sci. 2008, 47, 1347–1358. [Google Scholar] [CrossRef]

28. Baker, L.; Ellison, D. Optimisation of pedotransfer functions using an artificial neural network ensemble method. Geoderma 2008, 144, 212–224. [Google Scholar] [CrossRef]

29. Liu, H.; Xie, D.; Wu, W. Soil water content forecasting by ANN and SVM hybrid architecture. Env. Monit. Assess. 2008, 143, 187–193. [Google Scholar] [CrossRef]

30. Patil, S.L.; Tantau, H.J.; Salokhe, V.M. Modelling of tropical greenhouse temperature by auto regressive and neural network models. Biosyst. Eng. 2008, 99, 423–431. [Google Scholar] [CrossRef]

31. Xu, L.; Yang, J.; Zhang, Q.; Niu, H. Modelling water and salt transport in a soil–water–plant system under different groundwater tables. Water Environ. J. 2008, 22, 265–273. [Google Scholar] [CrossRef]

32. Zou, P.; Yang, J.; Fu, J.; Liu, G.; Li, D. Artificial neural network and time series models for predicting soil salt and water content. Agric. Water Manag. 2010, 97, 2009–2019. [Google Scholar] [CrossRef]

33. Stamenković, L.J. Application of ANN and SVM for prediction nutrients in rivers. J. Environ. Sci. Health Part A 2021, 56, 867–873. [Google Scholar] [CrossRef]

34. Stamenković, L.J.; Mrazovac Kurilić, S.; Presburger Ulniković, V. Prediction of nitrate concentration in Danube River water by ysing Artificial Neural Networks. Water Supply 2020, 20, 2119–2132. [Google Scholar] [CrossRef]

35. Jung, K.; Bae, D.-H.; Um, M.-J.; Kim, S.; Jeon, S.; Park, D. Evaluation of nitrate load estimations using neural networks and canonical correlation analysis with K-Fold Cross-Validation. Sustainability 2020, 12, 400. [Google Scholar] [CrossRef]

36. Band, S.S.; Janizadeh, S.; Pal, S.C.; Chowdhuri, I.; Siabi, Z.; Norouzi, A.; Melesse, A.M.; Shokri, M.; Mosavi, A. Comparative analysis of Artificial Intelligence models for accurate estimation of groundwater nitrate concentration. Sensors 2020, 20, 5763. [Google Scholar] [CrossRef]

37. Hrnjica, B.; Mehr, A.D.; Jakupovic, E.; Crnkic, A.; Hasanagic, R. Application of deep learning neural networks for nitrate prediction in the Klokot River, Bosnia and Herzegovina. In Proceedings of the 2021 7th International Conference on Control, Instrumentation and Automation (ICCIA), Tabriz, Iran, 23–24 February 2021; IEEE: Tabriz, Iran, 2021; pp. 1–6. [Google Scholar]

38. Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]

39. Al-Mahallawi, K.; Mania, J.; Hani, A.; Shahrour, I. Using of neural networks for the prediction of nitrate groundwater contamination in rural and agricultural areas. Environ. Earth Sci. 2012, 65, 917–928. [Google Scholar] [CrossRef]

40. Yesilnacar, M.I.; Sahinkaya, E.; Naz, M.; Ozkaya, B. Neural network prediction of nitrate in groundwater of Harran Plain, Turkiye. Environ. Geol. 2008, 56, 19–25. [Google Scholar] [CrossRef]

41. Elzain, H.E.; Chung, S.Y.; Senapathi, V.; Sekar, S.; Lee, S.Y.; Roy, P.D.; Hassan, A.; Sabarathinam, C. Comparative study of machine learning models for evaluating groundwater vulnerability to nitrate contamination. Ecotoxicol. Environ. Saf. 2022, 229, 113061. [Google Scholar] [CrossRef]

42. Stylianoudaki, C.; Trichakis, I.; Karatzas, G.P. Modeling groundwater nitrate contamination using artificial neural networks. Water 2022, 14, 1173. [Google Scholar] [CrossRef]

43. Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]

44. El Amri, A.; M’nassri, S.; Nasri, N.; Nsir, H.; Majdoub, R. Nitrate concentration analysis and prediction in a shallow aquifer in central-eastern Tunisia using artificial neural network and time series modelling. Environ. Sci. Pollut. Res. 2022, 29, 43300–43318. [Google Scholar] [CrossRef]

45. Deng, Y.; Ye, X.; Du, X. Predictive modeling and analysis of key drivers of groundwater nitrate pollution based on machine learning. J. Hydrol. 2023, 624, 129934. [Google Scholar] [CrossRef]

46. Sarangi, A.; Bhattacharya, A.K. Comparison of artificial neural network and regression models for sediment loss prediction from Banha watershed in India. Agric. Water Manag. 2005, 78, 195–208. [Google Scholar] [CrossRef]

47. Kim, M.Y.; Seo, M.C.; Kim, M.K. Linking hydro-meteorological factors to the assessment of nutrient loadings to streams from large-plotted paddy rice fields. Agric. Water Manag. 2007, 87, 223–228. [Google Scholar] [CrossRef]

48. Landeras, G.; Ortiz-Barredo, A.; López, J.J. Comparison of artificial neural network models and empirical and semi-empirical equations for daily reference evapotranspiration estimation in the Basque Country (Northern Spain). Agric. Water Manag. 2008, 95, 553–565. [Google Scholar] [CrossRef]

49. Chinh, L.V.; Hiramatsu, K.; Harada, M.; Mori, M. Estimation of water levels in a main drainage canal in a flat low-lying agricultural area using artificial neural network models. Agric. Water Manag. 2009, 96, 1332–1338. [Google Scholar] [CrossRef]

50. Chau, K.W. A review on integration of artificial intelligence into water quality modelling. Mar. Poll. Bull. 2006, 52, 726–733. [Google Scholar] [CrossRef]

51. Hatzikos, E.; Anastasakis, L.; Bassiliades, N.; Vlahavas, I. Applying neural networks with active neurons to sea-water quality measurements. In Proceedings of the Second International Scientific Conference on Computer Science, Varna, Bulgaria, 11–13 May 2005; IEEE Computer Society: Washington, DC, USA, 2005; pp. 114–119. [Google Scholar]

52. Wagh, V.; Panaskar, D.; Muley, A.; Mukate, S.; Gaikwad, S. Neural network modelling for nitrate concentration in groundwater of Kadava River basin, Nashik, Maharashtra, India. Groundw. Sustain. Develop. 2018, 7, 436–445. [Google Scholar] [CrossRef]

53. Latif, S.D.; Azmi, M.S.B.N.; Ahmed, A.N.; Fai, C.M.; El-Shafie, A. Application of artificial neural network for forecasting nitrate concentration as a water quality parameter: A case study of Feitsui Reservoir, Taiwan. Int. J. Des. Nat. Ecodynamics 2020, 15, 647–652. [Google Scholar] [CrossRef]

54. Meng, G.; Fang, L.; Yin, Y.; Zhang, Z.; Li, T.; Chen, P.; Liu, Y.; Zhang, L. Intelligent control of the electrochemical nitrate removal basing on artificial neural network (ANN). J. Water Process Eng. 2022, 49, 103122. [Google Scholar] [CrossRef]

55. Alsenjar, O.; Çetin, M.; Aksu, H.; Akgül, M.A.; Golpinar, M.S. Cropping pattern classification using artificial neural networks and evapotranspiration estimation in the Eastern Mediterranean region of Turkey. J. Agric. Sci. 2023, 29, 677–689. [Google Scholar] [CrossRef]

56. Alsenjar, O.; Cetin, M.; Aksu, H.; Golpinar, M.S.; Akgul, M.A. Actual evapotranspiration estimation using METRIC model and Landsat satellite images over an irrigated field in the Eastern Mediterranean Region of Turkey. Med. Geosc. Rev. 2023, 5, 35–49. [Google Scholar] [CrossRef]

57. Cetin, M.; Kaman, H.; Kirda, C.; Sesveren, S. Analysis of irrigation performance in water resources planning and management: A case study. Fresenius Environ. Bull. 2020, 29, 3409–3414. [Google Scholar]

58. Dinç, U.; Şenol, S.; Sayın, M.; Kapur, S.; Güzel, N.; Derici, R.; Yeşilsoy, M.Ş.; Yeğingil, D.; Sari, M.; Kaya, Z.; et al. The soils of Southeastern Anatolia Region (GAT) 1. Harran Plain. In TUBİTAK Agriculture and Forestry Group Guided Research Project Final Result Report; Project Number: TOAG-534; TÜBİTAK: Ankara, Türkiye, 1988. (In Turkish) [Google Scholar]

59. Karnez, E.; Sagir, H.; Gavan, M.; Golpinar, M.S.; Cetin, M.; Akgul, M.A.; İbrikci, H.; Pintar, M. Modeling Agricultural Land Management to Improve Understanding of Nitrogen Leaching in an Irrigated Mediterranean Area in Southern Turkey; IntechOpen: London, UK, 2017; ISBN 978-953-51-2882-3. [Google Scholar]

60. Rice, E.W.; Bridgewater, L. Standard Methods for the Examination of Water and Wastewater; American Public Health Association: Washington, DC, USA, 2012; Volume 10. [Google Scholar]

61. Karahan, H.; Iplikci, S.; Yasar, M.; Gurarslan, G. River flow estimation from upstream flow records using support vector machines. J. Appl. Math. 2014, 2014, 714213. [Google Scholar] [CrossRef]

62. Karahan, H.; Ayvaz, M.T. Simultaneous parameter identification of a heterogeneous aquifer system using artificial neural networks. Hydrogeol. J. 2008, 16, 817–827. [Google Scholar] [CrossRef]

63. Bilski, J.; Kowalczyk, B.; Marchlewska, A.; Zurada, J.M. Local Levenberg-Marquardt algorithm for learning feedforwad neural networks. J. Artif. Intell. Soft Comput. Res. 2020, 10, 299–316. [Google Scholar] [CrossRef]

64. Yan, Z.; Zhong, S.; Lin, L.; Cui, Z. Adaptive Levenberg–Marquardt algorithm: A new optimization strategy for Levenberg–Marquardt neural networks. Mathematics 2021, 9, 2176. [Google Scholar] [CrossRef]

65. Haring, M.; Grøtli, E.I.; Riemer-Sørensen, S.; Seel, K.; Hanssen, K.G. A Levenberg-Marquardt algorithm for sparse identification of dynamical systems. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 9323–9336. [Google Scholar] [CrossRef]

66. Souayeh, B.; Sabir, Z. Designing hyperbolic tangent sigmoid function for solving the Williamson nanofluid model. Fractal Fract. 2023, 7, 350. [Google Scholar] [CrossRef]

67. Pérez–Enríquez, L.; Zapotecas–Martínez, S.; Oliva, D.; Altamirano-Robles, L. Hyperbolic tangent sigmoid as a transformation function for image contrast enhancement. In Proceedings of the 2023 IEEE Symposium Series on Computational Intelligence (SSCI), Mexico City, Mexico, 5–8 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 282–287. [Google Scholar]

68. Rasamoelina, A.D.; Adjailia, F.; Sinčák, P. A review of activation function for artificial neural network. In Proceedings of the 2020 IEEE 18th World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herlany, Slovakia, 23–25 January 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 281–286. [Google Scholar]

69. Parhi, R.; Nowak, R.D. The role of neural network activation functions. IEEE Signal Process. Lett. 2020, 27, 1779–1783. [Google Scholar] [CrossRef]

70. Karahan, H.; Cetin, M.; Can, M.E.; Alsenjar, O. Developing a New ANN Model to Estimate Daily Actual Evapotranspiration Using Limited Climatic Data and Remote Sensing Techniques for Sustainable Water Management. Sustainability 2024, 16, 2481. [Google Scholar] [CrossRef]

Karahan H, Erkan Can M. A Novel Method to Forecast Nitrate Concentration Levels in Irrigation Areas for Sustainable Agriculture. Agriculture. 2025; 15(2):161. https://doi.org/10.3390/agriculture15020161

Перевод статьи «A Novel Method to Forecast Nitrate Concentration Levels in Irrigation Areas for Sustainable Agriculture» авторов Karahan H, Erkan Can M., оригинал доступен по ссылке. Лицензия: CC BY. Изменения: переведено на русский язык